|
Вакуум V ф= V Э=3*108 м/с l=300 м zc=120p=377 Ом |
Сравним параметры плоских волн в вакууме и меди при частоте f =1МГц.
В реальных проводниках электромагнитные волны испытывают сильное поглощение. Так в меди с f = 1МГц на пути в 1 мм затухание составит:
|
|
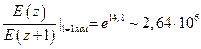 (8)
(8)
Металлы следует использовать при экранировании в переменном
электромагнитном поле.
Характерные параметры для проводящих сред.
Расстояние, на котором амплитуда волны уменьшается в е раз, называется
глубиной проникновения d, т.е.
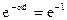 ;
; 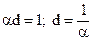 (1)
(1)
В общем случае: 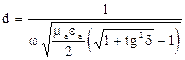 (2)
(2)
или для проводящих сред:
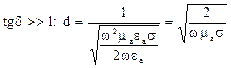 (3)
(3)
Отсюда следует, что w®d¯
Поляризация волн.
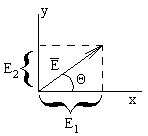
Для описания ориентации волн в пространстве вводят понятие поляризации. Под плоскостью поляризации подразумевают плоскость, проходящую через направление распространения волны и параллельно вектору 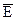 .
.
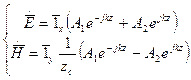 (1)
(1)
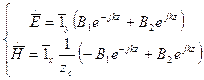 (2)
(2)
Для того чтобы проанализировать возможные случаи поляризации рассмотрим следующие решения. Пусть плоская волна представляет собой композицию решений из (1) и (2), которые также являются решением уравнения Гельмгольца.
|
|
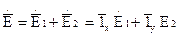 (3)
(3)
1. Пусть слагаемые в соотношении (3) синфазные, т.е. 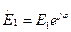 ;
; 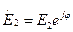 ;
;
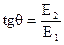 .
.
Тогда результирующий вектор 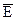 , а стало быть, и плоскость поляризации оказываются повернутыми на угол Q относительно оси x, причем положение плоскости поляризации в процессе распространения волны остается неизменным.
, а стало быть, и плоскость поляризации оказываются повернутыми на угол Q относительно оси x, причем положение плоскости поляризации в процессе распространения волны остается неизменным.
2. Пусть слагаемые равны по амплитуде, а по фазе отличаются на 90°:
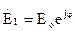 ,
, 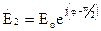 ,
,
тогда получим: 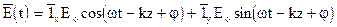
Определим положение угла Q: 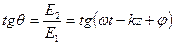
В этом случае положение плоскости поляризации изменяется во времени и пространстве. Если зафиксируем некоторую плоскость, то вектор 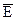 будет вращаться со скоростью V, и его конец будет описывать окружность. Если зафиксируем время, то вектор будет описывать спираль вдоль оси z. Этот случай поляризации называется круговой, т.е. в процессе распространения плоскость поляризации вращается. Это был случай левой поляризации. Для получения правой поляризации надо, чтобы
будет вращаться со скоростью V, и его конец будет описывать окружность. Если зафиксируем время, то вектор будет описывать спираль вдоль оси z. Этот случай поляризации называется круговой, т.е. в процессе распространения плоскость поляризации вращается. Это был случай левой поляризации. Для получения правой поляризации надо, чтобы
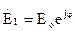 ,
, 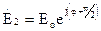 .
.
Условием круговой поляризации волны является временная и пространственная квадратура составляющих в соотношении (3). Компоненты должны быть взаимно ортогональны и должны отличаться по фазе на 90° и должно выполняться условие равенства амплитуд. В том случае, когда одно из условий не выполняется, имеем эллиптическую поляризацию. В любой фиксированной плоскости вектор Е движется по эллиптической замкнутой кривой. Степень поляризации характеризуют отношением большой оси к малой.
|
|
|
| Поделиться: |



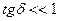 .
. 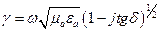 (1)
(1)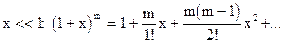
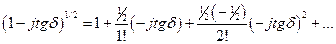 (2)
(2)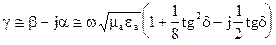 (3)
(3)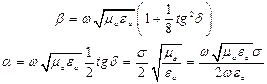 (4,5)
(4,5)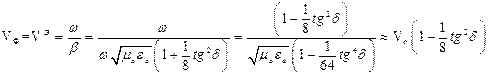 (6)
(6)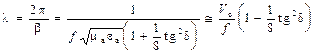
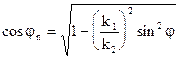
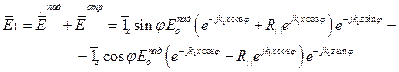 , х £ 0 (20)
, х £ 0 (20)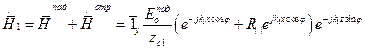 , х £ 0 (21)
, х £ 0 (21)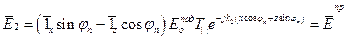 , х ³ 0 (22)
, х ³ 0 (22)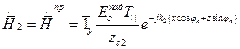 , х ³ 0 (23)
, х ³ 0 (23)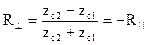
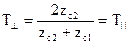
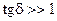 . Общее выражение:
. Общее выражение: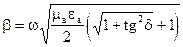 (1)
(1) 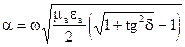 (2)
(2)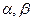 линейноым образо зависят от частоты):
линейноым образо зависят от частоты):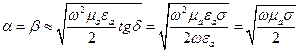 (3)
(3) (4) и для длины волны:
(4) и для длины волны: 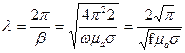 (5)
(5)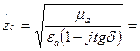
 (6)
(6)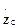 в виде реальной и мнимой частей:
в виде реальной и мнимой частей: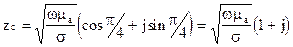 (7)
(7)