
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоские электромагнитные волны в однородной изотропной среде без потерь.Содержание книги
Поиск на нашем сайте
Будем рассматривать свободные (существующие без сторонних источников) гармонические колебания электромагнитного поля в однородной изотропной среде без потерь( Векторные уравнения (1) и (2) можно записать в виде системы из трех скалярных уравнений:
Наиболее просто уравнения (3) и (4) и их решения выглядят в случае плоских электромагнитных волн. Под плоскими волнами подразумевают электромагнитные волны, распространяющиеся вдоль линейной координаты, в каждый фиксированный момент времени неизменны в плоскости, перпендикулярной направлению распространения. Будем полагать, что волна, распространяется вдоль оси Z, т.е. вектор Пойнтинга: Из соотношения (5) видно, что вектор Пойнтинга определяется компонентами электромагнитного поля, находящимися в плоскости xOy. В данном случае отсутствуют составляющие поля вдоль оси z. Таким образом, должны выполняться условия: так как, по определению, поле должно быть неизменно в плоскости распространения волны, то: Используя соотношение (6), выражения (3) и (4) можно переписать следующим образом:
Решение каждого из уравнений: Для того, чтобы не увеличивать количество постоянных интегрирования мы компоненты поля
Используя соотношение (11), получим: Вынося jk за скобки, получим: Получим систему решений: Пары (16)-(17) и (18)-(19) образуют вектор Пойнтинга, ориентированный по оси z. Полученные нами, решения представляют собой сумму двух слагаемых (так как решалось дифференциальное уравнение). Уточним физический смысл каждого слагаемого. Для этого в уравнении (16) перейдем от комплексных амплитуд к мгновенным значениям.
Аргумент первого слагаемого — Рассмотрим аргументы и слагаемые для t=t1, z=z1, т.е.
Для того, чтобы оценить это смещение, осуществляем следующие равенства:
Приводя подобные члены в соотношениях (22) и (23), получим:
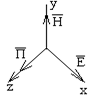
Выражая Соотношение (26) определяет перемещения фиксированной фазы Уточним физический смысл волнового числа k. Волновое число k показывает изменение фазы волны в радианах при прохождении волной пути в 1 метр. Минимальное расстояние, на котором фаза волны изменяется на 2p называется длинной волны (пространственным периодом). Проанализируем полученные решения на примере В этих общих решениях выделим слагаемые, которые соответствуют волне, распространяющейся в положительном направлении оси z: Перейдем к мгновенным значениям: 1. z = const — поверхность равных фаз представляет собой плоскость. 2. поверхность равных амплитуд совпадает с поверхностью равных фаз (плоская волна однородная). 3. в направлении распространения отсутствуют составляющие поля (плоская, однородная, поперечная). 4. компоненты поля плоской волны взаимноортогональны и перпендикулярны направлению распространения волны. Между составляющими поля плоской волны существует взаимосвязь.
Определим энергетические характеристики волны: Так как среда однородная, изотропная и без потерь,
Различные комбинации полного решения для плоской электромагнитной волны фактически соответствуют одной и той же плоской волне при различных ее ориентациях, относительно выбранной системы координат.
|
|||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 183; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.8.172 (0.009 с.) |

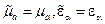 ). В этом случае для определения характеристик электромагнитного поля удобно воспользоваться однородными уравнениями Гельмгольца относительно векторов электромагнитного поля.
). В этом случае для определения характеристик электромагнитного поля удобно воспользоваться однородными уравнениями Гельмгольца относительно векторов электромагнитного поля. 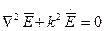 (1)
(1) 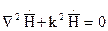 (2)
(2) 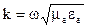 -волновое число.
-волновое число.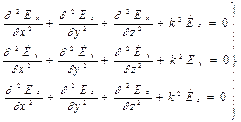 (3)
(3) 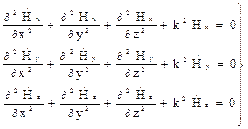 (4)
(4)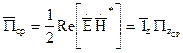 (5)
(5)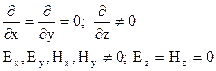 (6)
(6)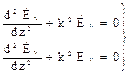 (7)
(7) 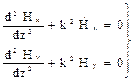 (8)
(8)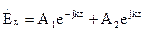 (9)
(9) 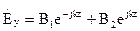 (10)
(10)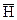 найдем с использованием решений (9), (10) и уравнений Максвелла.
найдем с использованием решений (9), (10) и уравнений Максвелла. 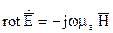
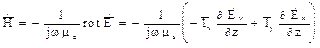 (11)
(11)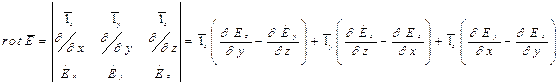
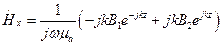 (12)
(12) 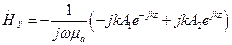 (13)
(13)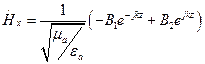 (14)
(14) 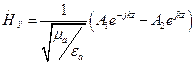 (15)
(15)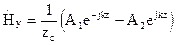 (17)
(17) 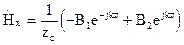 (19), где
(19), где 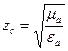 ,[Ом]-характеристическое сопр-ние среды,определяющееся св-ми среды.
,[Ом]-характеристическое сопр-ние среды,определяющееся св-ми среды.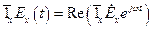
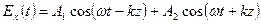 (20)
(20)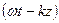 (21) Аргумент второго слагаемого —
(21) Аргумент второго слагаемого — 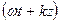
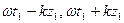 . Дадим приращение времени
. Дадим приращение времени 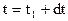 и определим смещение точек
и определим смещение точек 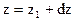 этого волнового процесса с постоянными фазами
этого волнового процесса с постоянными фазами 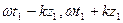 .
.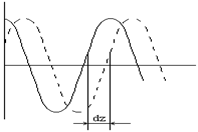
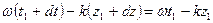 (22)
(22) 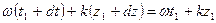 (23)
(23)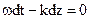 (24)
(24) 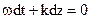 (25)
(25)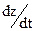 в первом и втором случаях, получаем:
в первом и втором случаях, получаем: 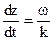 (26)
(26) 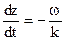 (27)
(27)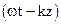 , а соотношение (27) —
, а соотношение (27) — 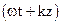 , т.е. соотношения (26) и (27) определяют фазовую скорость. Соотношение (26) определяет положительную фазовую скорость. Стало быть, компонента
, т.е. соотношения (26) и (27) определяют фазовую скорость. Соотношение (26) определяет положительную фазовую скорость. Стало быть, компонента 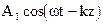 и соответствующая ей
и соответствующая ей 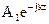 соответствуют плоской волне распространяющейся в положительном направлении оси z. Аналогично и соотношение (27). Итак, в полученном нами решении (16) первое слагаемое для плоской волны в положительном направлении, второе слагаемое — в отрицательном.
соответствуют плоской волне распространяющейся в положительном направлении оси z. Аналогично и соотношение (27). Итак, в полученном нами решении (16) первое слагаемое для плоской волны в положительном направлении, второе слагаемое — в отрицательном.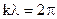 (28)
(28) 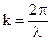 (29)
(29)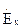 ,
, 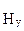 .
. 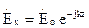 (30)
(30) 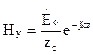 (31)
(31)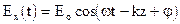 (32)
(32) 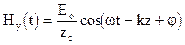 (33)
(33)
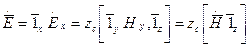
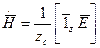
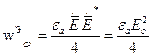 — объемная плотность электрической энергии.
— объемная плотность электрической энергии. 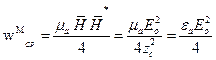 — объемная плотность магнитной энергии.
— объемная плотность магнитной энергии.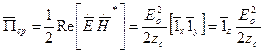 . Определим скорость распространения энергии:
. Определим скорость распространения энергии: 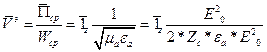 . Уравнение для фазовой скорости:
. Уравнение для фазовой скорости: 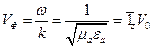 , где
, где 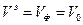 .
.



