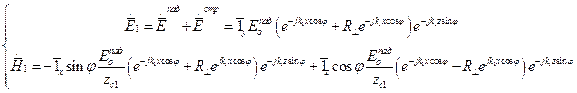Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоские волны произвольной ориентации.
В предыдущих параграфах мы рассматривали плоские волны, распространяющиеся вдоль осей декартовой системы. Признаком распространения является
Предполагаем, что среда без потерь.
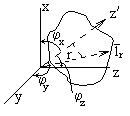
где Косинусы углов, определяющих направление волны, называются направляющими. Уравнение фазовой плоскости ( Где Тогда скалярное произведение:
Мы предполагали, что среда без потерь. В случае среды с потерями соотношения не меняются, только вместо k подставляется g =b — ja. Перед началом рассмотрения волновых явлений дадим ряд определений. Плоскость, проходящая через нормаль к границе раздела и параллельно направлению распространению волны, называется плоскостью падения. Вектор Не теряя обобщенности рассуждений, достаточно рассмотреть два случая ориентации 1.) 2.) При произвольной ориентации вектора
Падение плоской волны на границу раздела двух диэлектриков. Нормальная поляризация. Вводное замечание.
Рассмотрим падение плоской волны на плоскую границу раздела сред. Среды предполагаются без потерь. Будем полагать, что плоскость падения совпадает с плоскостью xOy декартовой системы координат. Угол между направлением распространения и осью x называется углом падения. Граница раздела сред совпадает с плоскостью yOz. Направляющие косинусы будут определяться следующим соотношением:
т.е. фазовый множитель:
Нормальная поляризация.
В общем случае: В данном случае вектор
Фазовый множитель:
Можно записать уравнение падающей волны. Подставляя предыдущие замечания в уравнения (1) и (2), получим:
В общем случае, в результате падения волны на границу, падающая волна полностью или частично отражается или преломляется. Естественно предположить, что отраженная и преломленная волны являются также плоскими, линейно поляризованными. Полагаем, что направление распространения падающей, отраженной и преломленной волн находится в плоскости xOz. Полагаем, что отраженная и преломленная волны, так же как и падающая, являются нормально поляризованными. Тогда для отраженной и преломленной волн можно записать:
где В данном случае являются известными характеристики падающей волны j, то, в соответствии с теоремой единственности, найденное решение будет верным и единственно возможным. Соотношения (9) должны выполняться во всех точках границы раздела, которая совпадает с осью z, т.е. при любых z граничные условия (9) должны выполняться. Это возможно, если падающая, отраженная и преломленная волны имеют одинаковую зависимость по z.
Учитывая, что угол j¢ имеет пределы При анализе подобных задач обычно предпочитают пользоваться не углом j¢, а дополняющим углом jо — углом отражения: Подставляя соотношение (13) в (12), получим: Воспользуемся соотношением (11) из которого следует, что:
Соотношение (15), записанное в форме (16), называется вторым закономСнелиуса. Отношение синуса угла отражения к синусу угла падения равно относительному коэффициенту преломления. Граничное условие (9) записывается следующим образом:
где учтено, что тангенциальные компоненты в первой среде образуются падающей и отраженной волнами, а тангенциальные компоненты во второй среде образуются преломленными волнами. Подставляя в соотношения (17), (18) соответствующие компоненты из соотношений (3) — (8), получим:
Учитывая одинаковую зависимость по z, можно отметить, что все фазовые множители одинаковые и их можно сократить. Кроме того,
Амплитуда отраженной и преломленной волн пропорциональна
Решая эту систему, получим:
Коэффициенты отражения и преломления часто называют коэффициентами Френеля. В соотношении (24) угол преломления можно исключить, используя закон Снелиуса.
Теперь можем записать результирующее поле в первой и второй средах, где учтено, что
Выражения для R и T справедливы, если одна или обе среды обладают конечной проводимостью.
|
|||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 59; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.121.160 (0.01 с.) |
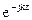 .
.
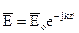
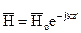

 ,
,  (1)
(1)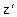 =const):
=const): 
 (2)
(2) (3)
(3) (4)
(4)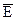 перпендикулярен направлению распространения волны, а относительно плоскости падения волны он ориентирован произвольным образом.
перпендикулярен направлению распространения волны, а относительно плоскости падения волны он ориентирован произвольным образом.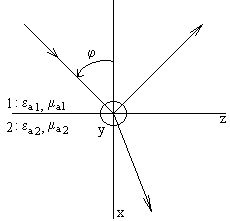

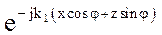 где
где 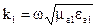
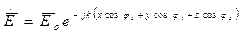 (1)
(1)  (2)
(2)
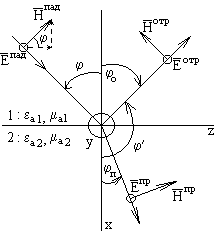
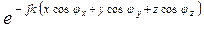
 ;
; 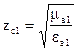
 (3)
(3) (4)
(4)
 (5)
(5)  (6)
(6) (7)
(7) 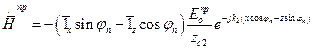 (8)
(8) ;
;  .
. . Искомыми являются j¢, jn,
. Искомыми являются j¢, jn,  ,
, 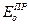 . Если в результате решения задачи нам удастся получить решение, которое удовлетворяет следующим граничным условиям:
. Если в результате решения задачи нам удастся получить решение, которое удовлетворяет следующим граничным условиям:  ;
;  (9)
(9) (10)
(10)  (11)
(11)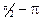 , а угол j имеет пределы
, а угол j имеет пределы 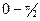 , мы делаем заключение, что:
, мы делаем заключение, что:  (12)
(12)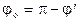 (13)
(13) (14) — первый закон Снелиуса.
(14) — первый закон Снелиуса. (15)
(15) 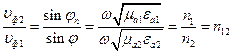 (16)
(16) , x = 0 (17)
, x = 0 (17)  , x = 0 (18)
, x = 0 (18)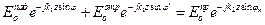 , x=0 (19)
, x=0 (19) , x=0 (20)
, x=0 (20) , получим:
, получим:  (21)
(21) (22)
(22) , т.е.
, т.е.  ,
,  — коэффициент отражения,
— коэффициент отражения,  — коэффициент преломления.
— коэффициент преломления.
 (23)
(23)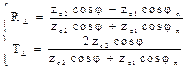 (24)
(24)
 и
и  :
: