Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторы электрического поля.Стр 1 из 24Следующая ⇒
Векторы магнитного поля. Сила взаимодействия электромагнитного поля на точечный электрический заряд зависит не только от величины и положения заряда, но также от скорости и направления его движения. Как известно, сила, действующая на положительный точечный электрический заряд движущийся в магнитном поле определяется силой Лоренца: где Магнитная сила пропорциональна скорости перемещения заряда и направлена перпендикулярно направлению движения заряда. Физический смысл: величина В различных средах силы взаимодействия магнитного поля на движущийся электрический заряд различны. Причина заключается в эффекте ненамагничиваемости вещества под действием внешнего магнитного поля. Очевидно, что магнитное поле действует не только на движущиеся положительные единичные заряды, но также и на проводники с током. На проводник длиной l, в котором протекает ток, действует сила:
В пределах рамки магнитное поле можно считать однородным (так как рамка мала): Моментсил
где Наряду с вектором магнитной индукции
где m0 = 4p*10-7 [Гн/м] - магнитная постоянная. При не очень сильных магнитных полях вектор
где
где, mа — абсолютная магнитная проницаемость среды:
Так как для вакуума магнитная восприимчивость равна нулю, то m0 называется абсолютной магнитной проницаемостью вакуума. Из рассмотренных с точки зрения магнитных свойств, среды можно классифицировать, анализируя величину магнитной восприимчивости: А) диамагнитная и парамагнитная среда — ½км½<<1. Б) диамагнитная среда — км<0. В) парамагнитная и ферромагнитная среда — км>0. Г) ферромагнитная среда — км>>1. В радиотехнике пользуются относительной магнитной проницаемостью:
Особенность вектора напряженности магнитного поля заключается в том, что при одинаковом расположении и величине магнитного поля векторное поле напряженности магнитного поля одинаково во всех средах.
Следует подчеркнуть, что (11) и (13) являются приближенными. В общем случае в ферромагнитных средах Будем полагать, что (11) и (13) во всех случаях справедливы. Особенность заключается в следующем: для диамагнитных и парамагнитных сред
Классификация сред. Свойства сред характеризуются электродинамическими параметрами, к которым относятся eа, mа, s (s — объемная удельная проводимость [См/м]). В зависимости от свойств электродинамические параметры среды делятся на: линейные и нелинейные. Среды, в которых электродинамические параметры не зависят от электрических и магнитных полей называются линейными. Среды, в которых наблюдается зависимость (eа, mа, s) = f (E,H) называются нелинейными. В природе все среды следует рассматривать как нелинейные. Тем не менее, большинство сред при малых полях со слабо выраженной зависимостью от величины поля для простоты полагают линейными. В свою очередь линейные среды делятся на: однородные, неоднородные, изотропные и анизотропные. Однородными называются среды, в которых электродинамические параметры не меняются от точки к точке, т.е. не являются функциями системы координат. Иначе — неоднородные. Изотропными называются среды, в которых электродинамические параметры одинаковы по всем направлениям. Анизотропными называются среды, в которых хотя бы один из параметров в некотором направлении имеет отличные электродинамические параметры. В изотропных средах электродинамические параметры являются постоянными скалярными величинами. В этих средах электрические векторы параллельны друг другу также как и магнитные.
В анизотропных средах эта параллельность нарушается. Причина заключается в следующем: вторичное поле, которое возникает в результате эффекта поляризации, оказывается направленным неколлинеарной с исходным полем (составляют некоторый угол). Для кристаллических диэлектриков анизотропия проявляется вследствие тензорного характера абсолютной диэлектрической проницаемости. При этом:
Аналогичное соотношение можно записать и для магнитного поля:
Уравнение непрерывности. В среде с током выделим некоторый объем V, ограниченный поверхностью S. В единицу времени через элементарную площадку Пусть за время Dt через поверхность прошел заряд dqэ, тогда
В свою очередь, полный электрический заряд, сосредоточенный в объеме:
В левой части последнего равенства переставим местами дифференцирование по времени и интегрирование по объему, это допустимо т.к. мы полагаем, что
В этом случае в левой части интегрирование и дифференцирование можно поменять местами: В выражении используется частная производная, так как r под интегралом является функцией не только координат, но и времени. Правую часть преобразуем по функции Остроградского – Гаусса: — это интегральное уравнение для произвольного объема V. Это возможно, если равны подынтегральные выражения:
Из него в частности следует, что истоками или стоками являются электрические заряды. Если мы предположим, что объемная плотность электрического заряда в объеме неизменна во времени, то производная по времени будет равна нулю, и мы придем к следующему соотношению:
Поле, которое характеризуется неизменными во времени векторными или скалярными величинами называется постоянным или стационарным. Из (2) следует, что постоянные токи не имеют истоков и стоков, а их силовые линии векторного поля являются замкнутыми.
Закон сохранения заряда. Полученное уравнение непрерывности тесно связано с законом сохранения заряда и по существу является его дифференциальной. Закон сохранения заряда: Всякому изменению электрического заряда (q) внутри объема V, ограниченному поверхностью S, соответствует электрический ток, втекающий или вытекающий из этого объема:
Для того, чтобы доказать взаимосвязь уравнения непрерывности и закона сохранения полного тока, получим закон сохранения полного тока из уравнения непрерывности. Проинтегрируем уравнение непрерывности по объему:
Левую часть преобразуем по теореме Остроградского - Гаусса, а в правой части поменяем интегрирование с дифференцированием: Здесь: Отсюда получаем: Пределы, ранее введенные, следует рассматривать в физическом смысле.
Третье уравнение Максвелла. Третье уравнение Максвелла является обобщением закона Гаусса на случай переменных процессов. Поток вектора электрической индукции
Учитывая, что Последнее соотношение справедливо, если равны подынтегральные соотношения. Отсюда получаем: Полученное соотношение и является третьим уравнением Максвелла.
Развернем дивергенцию в системе координат:
Анализируя (1) отметим, что истоками или стоками вектора электрического смещения
Подставим (2) в (1): Объемная плотность поляризационных зарядов: Причиной возникновения этой величины является неравномерность вещества под действием внешнего электрического поля. Подставляя (4) в (3), получим: Первое уравнение Максвелла.
В среде с постоянным током, который характеризуется вектором объемной плотности Для того, чтобы определить поле вектора Положительное направление обхода контура и единичной нормали связаны правилом правого винта. Напряженность магнитного поля можно определить, используя закон полного тока:
Запишем правую часть в интегральной форме:
Левую часть преобразуем по теореме Стокса (поверхность S произвольная):
Соотношение (3) называется дифференциальной формой закона полного тока для стационарного процесса. Возьмем дивергенцию левой и правой частей
Будем рассматривать случай переменного (нестационарный процесс) тока. Должно выполняться соотношение: Используя уравнение непрерывности, он получил: Далее он воспользовался своим третьим уравнением, т.е. он приписал: Полагаем, что функция
Подставляя (5) в (4'), получим: Выражение (6) является дифференциальной формой закона полного тока для нестационарного процесса. Слагаемое
Анализируя (6), Максвелл сформулировал одно из двух своих важнейших своих положений: Первое положение Максвелла: Переменное во времени электрическое поле приводит к появлению в пространстве магнитного поля.
Запишем (6) в виде проекций:
Дифференциальной форме (6) соответствует интегральная форма:
Второе уравнение Максвелла. В результате обобщения многочисленных экспериментальных исследований Фарадей получил закон электромагнитной индукции:
Переменное магнитное поле, пересекающее замкнутый проводящий контур, наводит в этом контуре э.д.с., величина которой пропорциональна скорости изменения потока.
Знак «-» говорит о том, что возбуждаемая в контуре Э.Д.С. как бы препятствует изменению магнитного потока (правило Ленца). Из (1) следует, что величина Э.Д.С. не зависит от материала, из которого изготовлен контур. Очевидно, что ток, возбуждаемый в контуре зависит от сопротивления проводника. Максвелл установил, что причиной возникновения э.д.с. в проводящем контуре является соленоидальное электрическое поле, которое возникает в пространстве и в отсутствие контура. Э.д.с. не зависит от свойств материала, но ток связан с его сопротивлением.
Магнитный поток, пересекающий поверхность S: Преобразуем левую часть, используя теорему Стокса:
Так как поверхность S и контур L выбраны произвольно, то Выражение (3) является дифференциальной формой обобщенного закона электромагнитной индукции, а выражение (2) — его интегральной формой. Второе положение Максвелла: Переменное магнитное поле возбуждает в пространстве соленоидальное электрическое поле.
Граничные условия для нормальных составляющих векторов электрического поля (Е и D). Поверхностные заряды.
На границе раздела двух сред, отличающихся объемом и диэлектрической проницаемостью, выделим элементарную площадку DS. Размеры ее настолько малы, что ее можно считать плоской. В пределах площадки нормальная составляющая вектора электрического смещения Применим к этому цилиндру 3-тье уравнение Максвелла в интегральной форме: Полную поверхность представим в виде суммы: Рассмотрим предел для левой части при
Осуществляя предельный переход при В данном соотношении следует рассмотреть 2 случая: 1. Пусть, на границе раздела S отсутствуют поверхностные заряды, тогда при любом конечном значении rэ (объемной плотности заряда) предел справа будет равен нулю и, получим: Из (7) следует, что при отсутствии поверхностного заряда на границе раздела S нормальная составляющая вектора электрического смещения Dn непрерывна при прохождении границы раздела. 2. Будем полагать, что электрические заряды распределены по поверхности S с поверхностной плотностью
В этом случае предел в правой части (6) можно преобразовать следующим образом: Равномерное распределение нормальной составляющей вектора D на границе раздела сред в пределах ∆S сопряжено с условием нормального распределения поверхностной плотности заряда в пределах ∆S.
Подставляя (8) в (6) получим, что при условии поверхностного распределения заряда граничное условие будет следующим:
Из (9) следует, что при наличии поверхностных зарядов на границе раздела нормальная компонента вектора D претерпевает разрыв величина которого определяется аовырхностной плотностью электрических зарядов. Переходя в (7) к напряжениям электрического поля получим:
Переходя в (9) к напряжениям электрического поля получим: P.S. Поверхностная плотность электрического заряда это удобная идеализация, упрощающая решение задач. Фактически электрический заряд распределен в конечном приграничном слое. Мы прибегаем к понятию плоскости поверхностного заряда, когда нас не интересует значение D в случае заряженного слоя.
18. Граничные условия для касательных составляющих векторов электрического поля (E и D). На границе раздела сред, отличающихся eа, выделим точку. Проведем через нее нормаль к поверхности S. Через эту нормаль проведем плоскость р. На линии пересечения плоскостей выделим элементарный отрезок Dl, так, чтобы его можно было считать прямолинейным, и касательная, составляющая Е в I и II средах у границы раздела, была распределена равномерно. Отрезок Dl включает точку, в которой построили единичную нормаль. В этой точке проведем единичный вектор
Представим контур в виде суммы отрезков:
Три единичных вектора связаны векторным соотношением. В слагаемых AB и CD векторные элементы dl равны, поэтому их можно заменить: АВ: CD: Найдем предел в соотношении (2) при Dh. Высоту уменьшим так, что бы АВ и CD были в разных средах. В пределе они совпадут с отрезком Dl.
так как вектор
С учетом отмеченных особенностей предельный переход при Dh®0,в соотношении (2), приводит к следующему соотношению:
На границе раздела сред тангенциальная составляющая напряженности электрического поля непрерывна:
Тангенциальная компонента вектора электрического смешения претерпевает разрыв, величина которого равна отношению диэлектрической проницаемости сред. Из полученных граничных условий следует, что на границе раздела сред, векторы электрического поля
Уравнения Гельмгольца. Практически все задачи электродинамики разделяют на 2 вида: 1. прямые задачи, в которых по заданному распределению сторонних источников необходимо определить соответствующее распределение электромагнитного поля. 2. обратные задачи, в которых по заданному распределению электромагнитного поля надо определить соответствующее распределение сторонних источников. В этом разделе рассмотрим основные методы решения прямых задач электродинамики применительно для гармонического ЭМ поля и однородных линейных изотропных сред. Относительно мгновенных значений векторов поля задачи решают очень редко, из-за сложности их определения. Обычно задачи решают для гармонических полей с использованием метода комплексных амплитуд. При решении любых электродинамических задач очень редко используют непосредственно уравнения Максвелла. Обычно уравнения Максвелла стараются свести к известным формам дифференциальных уравнений. Рассмотрим гармонический электромагнитный процесс. Запишем уравнения Максвелла для комплексных амплитуд:
Возьмем ротор от правой и левой части соотношения (1). Получим: Воспользуемся известным тождеством: Из 4-ого уравнения Максвелла: Подставим (4) и (2) в соотношение (3) и получим:
В результате проведенных преобразований мы получили неоднородное дифференциальное уравнение, которое в математической физике называется неоднородным уравнением Гельмгольца. Это уравнение описывает волновые процессы. Векторное дифференциальное уравнение (5) можно записать в виде трех уравнений проекций:
Аналогичные уравнения можно получить и для вектора напряженности поля.
Меняя везде знаки, получим: При анализе сред, в которых отсутствуют сторонние источники, неоднородные уравнения (5), (8) преобразуются в однородные:
Соотношения (5), (8), (9) называются уравнениями Гельмгольца относительно векторов поля.
Медь V ф= V Э=421 м/сек l=4,21*10-6 м zс=3,74*10-4 Ом |
|
Вакуум V ф= V Э=3*108 м/с l=300 м zc=120p=377 Ом |
Сравним параметры плоских волн в вакууме и меди при частоте f =1МГц.
В реальных проводниках электромагнитные волны испытывают сильное поглощение. Так в меди с f = 1МГц на пути в 1 мм затухание составит:
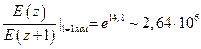 (8)
(8)
Металлы следует использовать при экранировании в переменном
электромагнитном поле.
Поляризация волн.
Для описания ориентации волн в пространстве вводят понятие поляризации. Под плоскостью поляризации подразумевают плоскость, проходящую через направление распространения волны и параллельно вектору 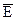 .
.
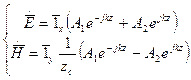 (1)
(1)
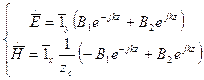 (2)
(2)
Для того чтобы проанализировать возможные случаи поляризации рассмотрим следующие решения. Пусть плоская волна представляет собой композицию решений из (1) и (2), которые также являются решением уравнения Гельмгольца.
|
|
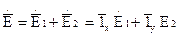 (3)
(3)
1. Пусть слагаемые в соотношении (3) синфазные, т.е. 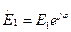 ;
; 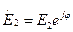 ;
;
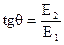 .
.
Тогда результирующий вектор 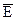 , а стало быть, и плоскость поляризации оказываются повернутыми на угол Q относительно оси x, причем положение плоскости поляризации в процессе распространения волны остается неизменным.
, а стало быть, и плоскость поляризации оказываются повернутыми на угол Q относительно оси x, причем положение плоскости поляризации в процессе распространения волны остается неизменным.
2. Пусть слагаемые равны по амплитуде, а по фазе отличаются на 90°:
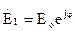 ,
, 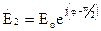 ,
,
тогда получим: 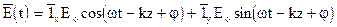
Определим положение угла Q: 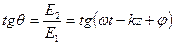
В этом случае положение плоскости поляризации изменяется во времени и пространстве. Если зафиксируем некоторую плоскость, то вектор 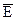 будет вращаться со скоростью V, и его конец будет описывать окружность. Если зафиксируем время, то вектор будет описывать спираль вдоль оси z. Этот случай поляризации называется круговой, т.е. в процессе распространения плоскость поляризации вращается. Это был случай левой поляризации. Для получения правой поляризации надо, чтобы
будет вращаться со скоростью V, и его конец будет описывать окружность. Если зафиксируем время, то вектор будет описывать спираль вдоль оси z. Этот случай поляризации называется круговой, т.е. в процессе распространения плоскость поляризации вращается. Это был случай левой поляризации. Для получения правой поляризации надо, чтобы
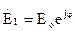 ,
, 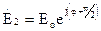 .
.
Условием круговой поляризации волны является временная и пространственная квадратура составляющих в соотношении (3). Компоненты должны быть взаимно ортогональны и должны отличаться по фазе на 90° и должно выполняться условие равенства амплитуд. В том случае, когда одно из условий не выполняется, имеем эллиптическую поляризацию. В любой фиксированной плоскости вектор Е движется по эллиптической замкнутой кривой. Степень поляризации характеризуют отношением большой оси к малой.
Нормальная поляризация.
В общем случае: 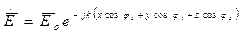 (1)
(1)  (2)
(2)
В данном случае вектор 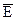 направлен так же как ось у.
направлен так же как ось у.

|
|
Фазовый множитель: 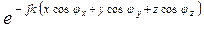
 ;
; 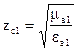
 (1),
(1),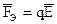 (2);
(2);  (3);
(3); 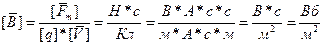 .
.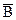 называется вектором магнитной индукции и равна силе, с которой магнитное поле действует на положительный точечный заряд, движущийся с единичной скоростью в направлении, перпендикулярном
называется вектором магнитной индукции и равна силе, с которой магнитное поле действует на положительный точечный заряд, движущийся с единичной скоростью в направлении, перпендикулярном  (4), где
(4), где  — электрический ток, протекающий по проводнику и совпадающий по направлению и направлением перемещения положительных зарядов в проводнике. Если в однородное магнитное поле внести рамку с током, то на нее будет действовать пара сил (момент сил):
— электрический ток, протекающий по проводнику и совпадающий по направлению и направлением перемещения положительных зарядов в проводнике. Если в однородное магнитное поле внести рамку с током, то на нее будет действовать пара сил (момент сил):
 (5)
(5) . Обычно рамки с током характеризуют магнитным моментом:
. Обычно рамки с током характеризуют магнитным моментом: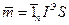 (6)
(6)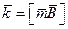 (7)
(7)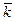 стремится повернуть рамку таким образом, чтобы вектор магнитного момента совпал с вектором
стремится повернуть рамку таким образом, чтобы вектор магнитного момента совпал с вектором 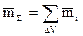 (8). В отсутствии внешнего магнитного поля магнитные моменты соответствующие отдельным атомам и молекулам ориентированы хаотически и поэтому
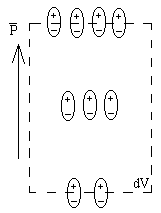
(8). В отсутствии внешнего магнитного поля магнитные моменты соответствующие отдельным атомам и молекулам ориентированы хаотически и поэтому  и собственное магнитное поле объема DV равны нулю. Под действием внешнего магнитного поля магнитные моменты, соответствующие отдельным атомам ориентируются по полю. Магнитные поля, соответствующие элементарным рамкам, складываются и накладываются на первичное магнитное поле. В результате наложения суммарное магнитное поле может быть больше или меньше исходного. Среды, в которых происходит уменьшение результирующего поля, называются диамагнитными. Среды, в которых происходит незначительное усиление, называются парамагнитными. Среды, в которых происходит значительное усиление, называются ферромагнитными. Эффект намагничивания среды внешним магнитным полем характеризуется вектором намагниченности, который определяют следующим образом:
и собственное магнитное поле объема DV равны нулю. Под действием внешнего магнитного поля магнитные моменты, соответствующие отдельным атомам ориентируются по полю. Магнитные поля, соответствующие элементарным рамкам, складываются и накладываются на первичное магнитное поле. В результате наложения суммарное магнитное поле может быть больше или меньше исходного. Среды, в которых происходит уменьшение результирующего поля, называются диамагнитными. Среды, в которых происходит незначительное усиление, называются парамагнитными. Среды, в которых происходит значительное усиление, называются ферромагнитными. Эффект намагничивания среды внешним магнитным полем характеризуется вектором намагниченности, который определяют следующим образом: (9),
(9),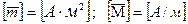 .
.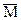
 для описания используют напряженность магнитного поля:
для описания используют напряженность магнитного поля: (10);
(10);  ;
; пропорционален вектору
пропорционален вектору 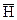 :
: (11)
(11) — магнитная восприимчивость среды (безразмерный коэффициент, характеризующий среду). Подставляя (11) в (10), получим:
— магнитная восприимчивость среды (безразмерный коэффициент, характеризующий среду). Подставляя (11) в (10), получим: (12)
(12) (13),
(13), .
.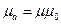 ;
;  (14).
(14).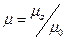 (15)
(15)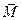 зависит не только от величины магнитного поля в данный момент, но также и от величины магнитного поля в предыдущие моменты (явление Гистерезиса).
зависит не только от величины магнитного поля в данный момент, но также и от величины магнитного поля в предыдущие моменты (явление Гистерезиса).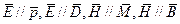
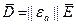 ,
, 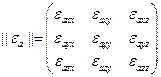 , где
, где  - тензорная диэлектрическая проницаемость. При этом взаимосвязь сохраняет следующий вид. Последнее выражение, с учетом тензорного характера, может быть записано в виде:
- тензорная диэлектрическая проницаемость. При этом взаимосвязь сохраняет следующий вид. Последнее выражение, с учетом тензорного характера, может быть записано в виде: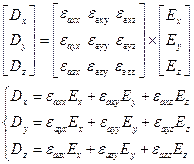 .
. 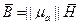

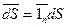 проходит заряд
проходит заряд 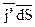 , а через всю поверхность S проходит заряд:
, а через всю поверхность S проходит заряд:  .
. .
.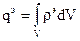 ,
, 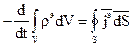 .
.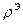 и ее производные непрерывны в каждой точке. Будем полагать, что функция rэ характеризует распределение электрического заряда в объеме.
и ее производные непрерывны в каждой точке. Будем полагать, что функция rэ характеризует распределение электрического заряда в объеме. .
. .
.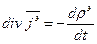 — уравнение непрерывности (1).
— уравнение непрерывности (1). (2).
(2). (1).
(1).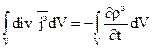 .
.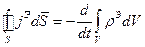 .
.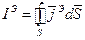 , а
, а 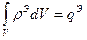 .
.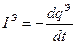 .
.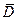 через поверхность S, ограниченную объемом V равен электрическому заряду сосредоточенному внутри объема V:
через поверхность S, ограниченную объемом V равен электрическому заряду сосредоточенному внутри объема V: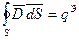 .
. получим
получим 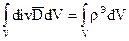 .
. (1).
(1).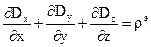 .
.
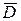 являются свободные электрические заряды. Силовые линии начинаются на положительных зарядах и заканчиваются на отрицательных. В отличие от вектора электрического смещения истоками и стоками другого электрического вектора - вектора напряженности
являются свободные электрические заряды. Силовые линии начинаются на положительных зарядах и заканчиваются на отрицательных. В отличие от вектора электрического смещения истоками и стоками другого электрического вектора - вектора напряженности 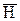 могут быть как свободные, так и связанные электрические заряды.
могут быть как свободные, так и связанные электрические заряды. (2).
(2). (3).
(3).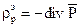 (4).
(4). (5).
(5).
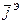 , выделим некоторый замкнутый контур V и поверхность S, которая опирается на этот контур. Введем положительную единичную нормаль к поверхности S.
, выделим некоторый замкнутый контур V и поверхность S, которая опирается на этот контур. Введем положительную единичную нормаль к поверхности S.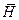 необходимо воспользоваться законом Ампера или законом полного тока.
необходимо воспользоваться законом Ампера или законом полного тока.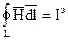 (1).
(1).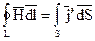 (2).
(2). .
. (3)
(3) :
: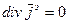 (4).
(4). . Однако выполнялось соотношение (4). Максвелл добавил некую величину Y и получил:
. Однако выполнялось соотношение (4). Максвелл добавил некую величину Y и получил: 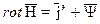 ;
;  (4').
(4'). .
.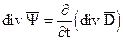 .
.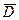 и её производная непрерывны в каждой точке пространства. В последнем соотношении поменяем дифференцирование в пространстве и дифференцирование по времени:
и её производная непрерывны в каждой точке пространства. В последнем соотношении поменяем дифференцирование в пространстве и дифференцирование по времени: 
 (5)
(5)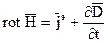 (6).
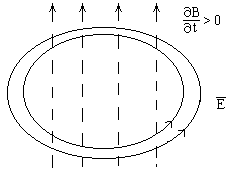
(6). имеет смысл объемной плотности электрического тока. Вектор объемной плотности тока смещения:
имеет смысл объемной плотности электрического тока. Вектор объемной плотности тока смещения: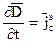
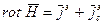 (7).
(7).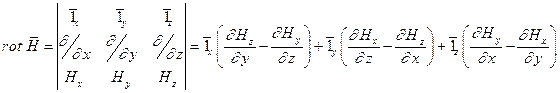
 (6')
(6')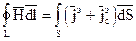 (8).
(8).
 (1)
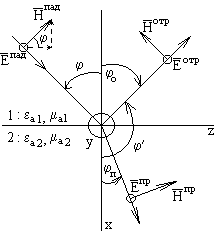
(1) Интеграл по замкнутому контуру (рисунок правовинтовой системы) не равен нулю. Рассмотрим в пространстве некий контур l, поверхность S, на которую опирается этот контур и единичную нормаль. Положительное направление обхода связано с направлением единичной нормали правилом правого винта. Магнитный поток, пересекающий контур, считается положительным или отрицательным в зависимости от того, совпадает он или нет с направлением единичной нормали. Скорость изменения магнитного потока считается положительной или отрицательной в зависимости от того, увеличивается или уменьшается магнитный поток. Запишем обобщения для электромагнитной индукции через вектора электромагнитного поля:
Интеграл по замкнутому контуру (рисунок правовинтовой системы) не равен нулю. Рассмотрим в пространстве некий контур l, поверхность S, на которую опирается этот контур и единичную нормаль. Положительное направление обхода связано с направлением единичной нормали правилом правого винта. Магнитный поток, пересекающий контур, считается положительным или отрицательным в зависимости от того, совпадает он или нет с направлением единичной нормали. Скорость изменения магнитного потока считается положительной или отрицательной в зависимости от того, увеличивается или уменьшается магнитный поток. Запишем обобщения для электромагнитной индукции через вектора электромагнитного поля: 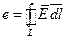 .
. . Подставляя эти соотношения в выражение (1), получим:
. Подставляя эти соотношения в выражение (1), получим:  (2).
(2).
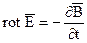 (3).
(3).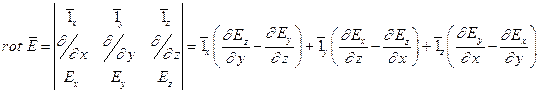
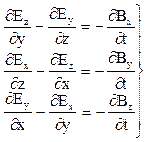

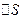 была распределена равномерно. На DS, как на основании, построим прямой цилиндр высотой Dh так, чтобы его основания (
была распределена равномерно. На DS, как на основании, построим прямой цилиндр высотой Dh так, чтобы его основания (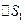 и
и 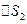 ) находились в различных средах. Единичный вектор
) находились в различных средах. Единичный вектор 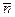 - нормаль к основанию
- нормаль к основанию 
 (1)
(1)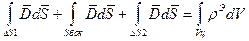 (2)
(2) . Устремим
. Устремим 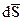 совпадает с направлением внешней нормали к поверхности цилиндра для слагаемых, в левой части получим следующее предельное соотношение:
совпадает с направлением внешней нормали к поверхности цилиндра для слагаемых, в левой части получим следующее предельное соотношение: (3)
(3)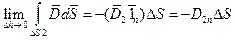 (4)
(4)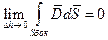 (5)
(5) (6).
(6). (7)
(7) .
.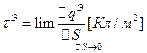
 .
.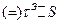 (8).
(8).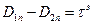 (9)
(9)  .
. или
или  (10)
(10) (11) – справедливо при наличии поверхностных зарядов. Из (10) и (11) следует, что даже при отсутствии поверхностных зарядов нормальная компонента вектора Е претерпевает разрыв, величина которого определяется соотношением диэлектрических проницаемостей сред. Наличие поверхностных зарядов изменяют величину этого разрыва.
(11) – справедливо при наличии поверхностных зарядов. Из (10) и (11) следует, что даже при отсутствии поверхностных зарядов нормальная компонента вектора Е претерпевает разрыв, величина которого определяется соотношением диэлектрических проницаемостей сред. Наличие поверхностных зарядов изменяют величину этого разрыва.
 касательный к Dl и единичный вектор
касательный к Dl и единичный вектор 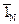 перпендикулярный к Dl. В плоскости р построим контур высотой Dh так, чтобы участки контура CD и АВ находились в разных средах. Положительное направление обхода контура ABCD связано с направлением единичной нормали
перпендикулярный к Dl. В плоскости р построим контур высотой Dh так, чтобы участки контура CD и АВ находились в разных средах. Положительное направление обхода контура ABCD связано с направлением единичной нормали 
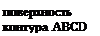
 (1)
(1)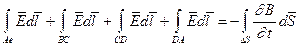 (2)
(2)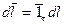

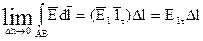
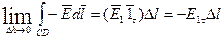

 (3)
(3) (4)
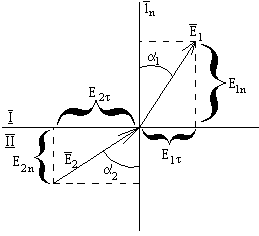
(4)
 преломляются.
преломляются.
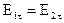
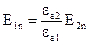

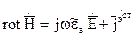 (1)
(1) 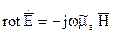 (2)
(2) (3)
(3)
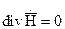 следует, что:
следует, что:  (4)
(4)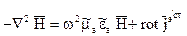 или
или (5)
(5)
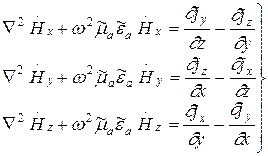 (6)
(6) (7)
(7) 
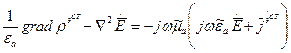

 (8)
(8) (9)
(9)