
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементарные щелевые излучатели.⇐ ПредыдущаяСтр 24 из 24
Рассматриваемая система называется двухсторонняя излучающая щель. Существуют способы одностороннего возбуждения щели. Необходимо решить задачу о возбуждении электромагнитного поля малым током, протекающим в щели. Наибольший интерес представляет электромагнитное поле в ДЗ относительно щели gr>>1. Типовой алгоритм решения задачи: Решить неоднородное уравнение Гельмгольца относительно векторного магнитного потенциала. Затем, используя уравнение связи, по найденным значениям векторного магнитного потенциала надо вычислить составляющие электромагнитного поля. Т. к. нас интересует ДЗ, то в этих выражениях необходимо осуществить предельный переход, полагая gr>>1. Но решение подобной задачи существенно упрощается, если воспользоваться принципом перестановочной двойственности: выпишем найденные раннее выражения для ЭЭИ: ЭЭИ:
ЭМИ:
Знак “—” говорит о том, что Е распространяется в положительном направлении радиальной координаты.
Из (4) следует, что в ДЗ электрическое поле ЭМИ имеет только j-ую составляющую, что свидетельствует о том, что в ДЗ электрическое поле, постепенно деформируясь, превращается в окружность. При анализе щелевых излучателей пользуются напряжением в щели, а не формальным магнитным током.
Постараемся перейти от магнитного тока к напряжению. В соответствии с законом полного тока
Размеры пластины малы, толщина исчезающе мала, т. е. в пределах этой пластины Нt можно считать неизменной. Интегрирование по поверхности в данном случае заменяется интегрированием по участкам. Контур предполагается совпадающим с контуром поперечного сечения. Вычислим напряжение в щели:
К (5) применим принцип перестановочной двойственности
Из сопоставления (6) и (7) следует
Откуда Переходя к соотношения (3), (4) от (8) получим:
Вычислим мощность излучения ЭМИ (вычислим П и проинтегрируем его по контуру).
Выражение из электротехники:
Из сопоставления (11) и (12) следует:
Для вакуума или воздуха:
Представляет интерес сравнить характеристики ЭЭИ и ЭМИ. Будем предполагать, что оба они излучают одинаковую мощность, тогда: Для определенности зададим IЭ=1 А. Из этого соотношения следует, сто напряжение в щели Uщ=188 В. Из последних рассуждений следуют недостатки щелевых излучателей:
Для излучения большой мощности напряжение щели должно быть велико, в свою очередь напряжение ограничено величиной пробоя в среде при заданных условиях. Щелевой излучатель является неединственным вариантом ЭМИ. В качестве ЭМИ могут рассматриваться элементарные рамки с электрическим током (периметр рамки должен быть << l). В этом случае можно полагать, что перпендикулярно поверхности рамки протекает магнитный ток.
Лемма Лоренца. Лемма Лоренца устанавливает взаимосвязь между разнесенными в пространстве сторонними источниками и возбуждаемыми ими электромагнитными полями. Предположим, что в точке 1 находится сторонний источник, который характеризуется В точке 2 расположен другой источник Очевидно, что взаимосвязь между ними может быть описана уравнениями Максвелла:
Аналогично для второго источника:
(1) скалярно умножим на
(2) умножим скалярно на
Вспомним известное векторное тождество:
Используя его (5) и (6) можно переписать следующим образом:
Из (7) вычтем (8):
(9) называется леммой Лоренца в дифференциальной форме (соотношение справедливо в каждой точке пространства, где имеются сторонние источники). Проинтегрируем (9) по объему который включает все сторонние источники:
Левую часть (10) преобразуем, используя теорему Остроградского-Гаусса. В соответствии с этой теоремой:
где S1 — замкнутая поверхность, ограничивающая объем. Тогда, с учетом (11), соотношение (9) запишется в следующем виде:
(12) — лемма Лоренца для ограниченного объема. Рассмотрим случай бесконечного увеличения объема V1. При этом поверхность S1 размещается в бесконечно удаленных точках относительно расположения сторонних источников. В случае неограниченного объема V1 поверхностный интеграл в (12) равен 0. Это можно объяснить, используя 2 аргумента: 1) поверхность S1 удалена на бесконечность. Скорость распространения имеет конечное значение, т. е. за любой конечный промежуток времени волны не смогут достигнуть поверхности S1, т. е. на поверхности S1 отсутствуют составляющие поля, а, следовательно, интеграл по этой поверхности будет равен нулю 2) как нам известно в ДЗ амплитуда составляющих поля убывает пропорционально 1/r. В случае реальных сред, которые характеризуются малыми, но конечными по величине потерями, амплитуда убывает еще быстрее. Таким образом, в реальных средах векторное произведение
Таким образом в случае неограниченного объема V1 лемма Лоренца записывается в следующей форме:
|
|||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.64.128 (0.015 с.) |
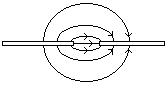
 Рассмотрим бесконечно металлический экран, в котором прорезана узкая щель. Предположим, что она возбуждается от источника гармонических колебаний. Можно предположить, что в этой щели протекает переменный магнитный ток. С тем, чтобы этот магнитный излучатель был элементарным, следует положить, что l<<l (D<<l).
Рассмотрим бесконечно металлический экран, в котором прорезана узкая щель. Предположим, что она возбуждается от источника гармонических колебаний. Можно предположить, что в этой щели протекает переменный магнитный ток. С тем, чтобы этот магнитный излучатель был элементарным, следует положить, что l<<l (D<<l).

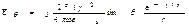 (1)
(1) (2)
(2)


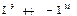
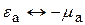
 (3)
(3) (4)
(4)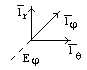

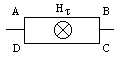
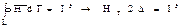 (5)
(5)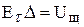 (6)
(6) (7)
(7)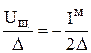
 (8)
(8) (9)
(9)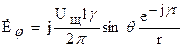 (10)
(10)

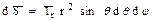
 (11)
(11)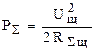
 (12)
(12)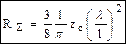 (13)
(13)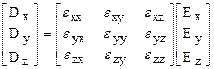 [Ом]
[Ом]

 ,
,  ,
,  ,
,  .
.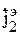 ,
,  ,
, 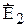 ,
,  .
.
 (1)
(1)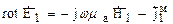 (2)
(2) (3)
(3) 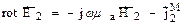 (4)
(4) (4) умножим на
(4) умножим на  (5)
(5)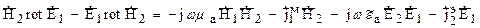 (6)
(6)

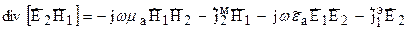 (7)
(7) (8)
(8)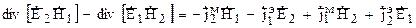 (9)
(9) (10)
(10)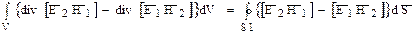 (11)
(11)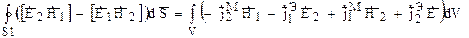 (12)
(12) в ДЗ убывает быстрее, чем 1/r2. Площадь сферы с ростом r возрастает пропорционально r2. Таким образом, предел при
в ДЗ убывает быстрее, чем 1/r2. Площадь сферы с ростом r возрастает пропорционально r2. Таким образом, предел при  :
:
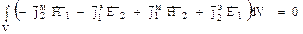 (13)
(13)


