Особенности термодинамической пары.

 

       Форму движения, которую будем именовать термодинамической парой, еще удается изучить достаточно подробно и указать основные специфические законы, которым она подчиняется. За явлением пары классификация движения содержит пропуски, о которых пока ничего определенного сказать нельзя.

       Явление термодинамической пары весьма универсально. Природа широко использует его в живых организмах для транспорта питательных веществ, для процессов обмена и т.д. Оно находит также применение в технике. Общая теория пары была описана в первых изданиях работы [5].

       Суть явления термодинамической пары заключается в следующем.

 

 

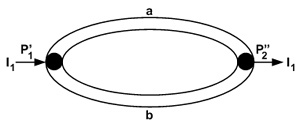
Рис. 40. Схема соединения проводников а и b в термодинамической паре.

 

       Если (например, при n = 2) соединить концами два родственных проводника а и b и создать между спаями (на рис. 40 зачернены) разность первого потенциала

                                           DР₁ = Р₁ ” – Р ₁ ’,

то в полученной таким образом цепи – системе возникнут все те эффекты, о которых говорилось в прежних главах. В частности, в замкнутой цепи начинается круговая циркуляция второго заряда. Непрерывные круговые изменения движения происходят по определенной (фиксированной) программе. Интенсивность движения определяется разностью значений первого потенциала. В спаях пары образуются скачки второго потенциала. В ее ветвях наблюдаются линейные эффекты. Циркуляция второго заряда в спаях и ветвях сопровождается положительными и отрицательными эффектами трения (плюс- и минус-диссипация), увлечения и т.д. [4, 5].

 

       2. Фильтрационная пара.

 

       Газ, жидкость или твердое тело, заполняющее капилляр – трубку с тонким отверстием, - тоже представляют собой термодинамическую пару. Будем называть ее фильтрационной. Пристеночный (точнее капиллярный) слой вещества толщиной x₀, испытывающий молекулярное взаимодействие с материалом капилляра, играет роль проводника b, осевой слой вещества, не испытывающий такого взаимодействия, - роль проводника а. Проводники а и b обладают неодинаковыми значениями коэффициентов А в уравнениях состояния. Спаями (местами контакта проводников а и b) служат концы капилляра.

       Если между спаями создать разность некоторого потенциала DР₁, то в цепи появятся все эффекты, присущие обычной паре, а также два новых – фиктивной движущей силы и разделения. Вторым (циркулирующим) зарядом в большинстве случаев служит само вещество, заполняющее капилляр: в пристеночном слое оно фильтруется или диффундирует в одном направлении (на рис. 41 влево), а в осевом – в другом направлении (вправо).

 

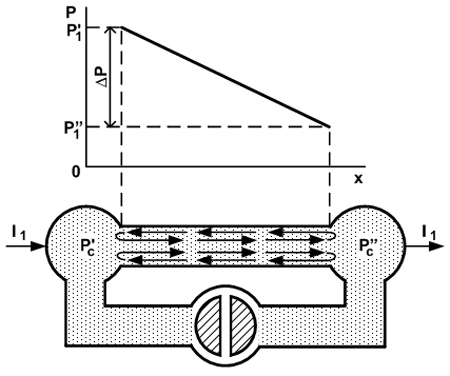
       Рис. 41. Схема действия фильтрационной пары.

 

       Пристеночный слой играет роль насоса, поэтому, если на концах капилляра имеются емкости конечных размеров второго заряда, то происходит переток вещества из одной емкости в другую и появление между емкостями разности давлений:

                                           Dр_с = р_с ” – р_с ’        н/м².                                               (786)

       Это есть эффект возникновения фиктивной движущей силы.

       Циркуляция сложного по составу вещества сопровождается эффектом разделения: концентрация отдельных компонентов смеси в разных емкостях получается не одинаковой.

       Капиллярнопористое тело содержит в себе большое число пор и капилляров. Поэтому в нем наблюдаются те же эффекты, что и в отдельном капилляре.

 

 

Теория пары.

 

Обобщенная пара.

 

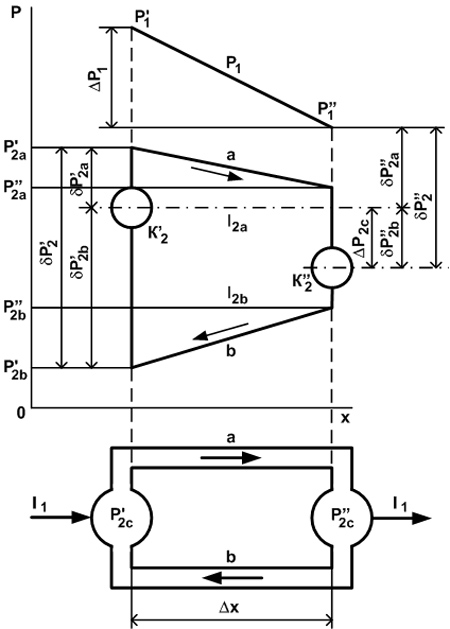
       На рис. 42 изображена схема обобщенной термодинамической пары, в которой места спаев обладают емкостями (резервуарами) второго заряда (К₂ ’ и К₂ ”). В общем случае между каждой емкостью и проводниками а и b имеются свои скачки второго потенциала.

 

                   Рис. 42. Схема действия обобщенной термодинамической пары.

Суммарные скачки в первом и втором спаях

       dР₂ ’ = dР_{2 a} ’ + dР_{2 b} ’ = Р_{2 a} ’ - Р_{2 с} ’ + Р_{2 с} ’ - Р_{2 b} ’ = Р_{2 a} ’ - Р_{2 b} ’;         (787)

       dР₂ ” = dР_{2 a} ” + dР_{2 b} ” = Р_{2 с} ” - Р_{2 а} ” + Р_{2 b} ” - Р_{2 c} ” = Р_{2 d} ” - Р_{2 a} ”.   (788)

       Фиктивная движущая сила определяется разностью

                                           DР_{2 c} = Р_{2 c} ” - Р_{2 с} ’.                                                               (789)

       Обобщенная пара охватывает все основные случаи, встречающиеся на практике. В частности, она описывает фильтрационную пару (рис. 41). Если емкости К₂ ’ и К₂ ” равны нулю, то получается пара, изображенная на рис. 40.

       Рассмотрим теперь количественные соотношения, характеризующие работу термодинамической пары.

 

       2. Полная движущая сила.

 

       Энергию, необходимую для поддержания циркуляции второго заряда, поставляют окружающая среда и (частично) движущийся первый заряд. В обычных условиях главную долю энергии дают эффекты контактной диссипации и линейный. В излагаемой ниже теории для простоты не учитывается эффект контактного заряжания второго заряда другими зарядами, т.е. принимается, что в спаях имеются скачки только второго потенциала. Кроме того, не учитываются эффекты второго порядка, например, линейного заряжания первого заряда вторым и т.д.

       Суммарные контактные (в спаях) и линейные (в проводниках) работы второго заряда определяются выражениями [см. формулы (627) и (644)]:

                   dQ_2к = dQ_2д ” - dQ_2д ’ = dР₂ ”dЕ₂ - dР₂ ’dЕ₂ = dР_{2 к} dЕ₂     дж;             (790)

                   dQ_21л = dQ_{21 b} - dQ_21а = b_21b DР₁ I₂²dЕ₂ - b_21а DР₁ I₂²dЕ₂ = dР_2л dЕ₂ дж, (791)

где

                                           dР_{2 к} = dР₂ ” - dР₂ ’;                                                            (792)

                                           dР_2л = dР_21b - dР_21а = (b_21b - b_21а) DР₁I₂².                          (793)

       Следовательно, полная полезная работа циркуляции второго заряда

                   dQ₂ = dQ_2к + dQ_2л = (dР_2к + dР_2л)dЕ₂ = dР₂dЕ₂            дж,             (794)

где полная движущая сила термодинамической пары

                                           dР₂ = dР_2к + dР_2л.                                                              (795)

       Контактная составляющая движущей силы пары может быть выражена через разность DР₁ первого потенциала с помощью уравнения состояния. Например, при dЕ₂ = 0 из уравнения (106) находим

                                           dР₂ = (А₂₁/А₁₁)dР₁.                                                            (796)

       Для тел а и b имеем

                                           dР_2а = (А_21а/А_11а)dР_1а;                                                      (797)

                                           dР_2b = (А_{21 b}/А_11b)dР_1b.                                                      (797)

       Если пренебречь скачками первого потенциала в спаях (dР_1а = dР_1b = dР₁; Р_1а = Р_1b = Р₁), тогда контактная движущая сила

                                           D(dР_2к) = dР_{2 b} - dР_2а = Ф₂₁ dР₁.                                        (798)

или (для конечного, но малого изменения потенциалов)

                                           dР_2к = dР₂ ” - dР₂ ’ = Ф₂₁ DР₁,                                                       (799)

где

                                           Ф₂₁ = (А_{21 b}/А_11b) - (А_21а/А_11а).                                           (800)

       Окончательно полная движущая сила пары может быть представлена в виде [формулы (793), (795) и (799)]:

                                           d(dР₂)/dР₁ = Ф₂₁ - (b_21b - b_21а)I₂².                                      (801)

       У идеальных тел коэффициенты А постоянны, поэтому потенциалы Р_2а и Р_2b пропорциональны потенциалу Р₁, и следовательно, коэффициент [формулы (796) – (799)]

                                           Ф₂₁ = d(dР_2к)/dР₁ = dР_2к/ DР₁ = dР₂’/Р₁’ = dР₂”/Р₁”.      (802)

       Дифференцирование выражения (801) дает (Ф = const):

                                           d²(dР₂)/dР₁² = (b_21b - b_21а)I₂².                                 (803)

       Эта формула связывает между собой полную и линейную составляющие движущей силы.

       Движущая сила пары расходуется на преодоление сопротивлений цепи. Если пренебречь сопротивлениями спаев, тогда связь между движущей силой, перепадами потенциала в проводниках а и b

                                           DР_2а = Р_2а” - Р_2а ’;                                                              (804)

                                           DР_2b = Р_2b” - Р_2b’                                                               (804)

и сопротивлениями проводников

                                           R_2а = D х_а/(F_аL_2а);                                                              (805)

                                           R_2b = D х_b/(F_bL_2b)                                                               (805)

найдется с помощью выражений:

                                           DР_2а = I_2а R_2а + dР_21а;                                                        (806)

                                           DР_{2 b} = I_{2 b} R_2b - dР_{21 b}.                                                         (806)

       При I_2а = I_{2 b} = I₂ получаем

                                           dР₂ = I₂(R_2а + R_2b) = DР_2а + DР_{2 b} + dР_2л                         (807)

или

                                           dР_2к = DР_2а + DР_2b.                                                           (808)

       Сумма измеренных перепадов второго потенциала вдоль проводников равна контактной составляющей движущей силы.

 

       3. Эффект возникновения фиктивной движущей силы.

 

       Под действием движущей силы dР₂ в паре происходит циркуляция второго заряда и появляется фиктивная движущая сила DР_2с. Для ее определения представим полную движущую силу пары в виде

                                           dР₂ = dР_2а + dР_2b,                                                             (809)

где dР_2а - движущая сила верхнего участка пары (над емкостями, рис. 42),

                                           dР_2а = - dР_2а ’ - dР_21а + dР_2а ”;                                           (810)

dР_2b - движущая сила нижнего участка (под емкостями),

                                           dР_{2 b} = - dР_{2 b} ’ - dР_{21 b} + dР_{2 b} ”.                                           (811)

       Через эти частные движущие силы можно найти потоки второго заряда в проводниках а и b с помощью выражений:

                                           I_2а = (dР_2а + DР_2с)/ R_2а;                                                      (812)

                                           I_{2 b} = (dР_{2 b} - DР_2с)/ R_2b.                                                  (812)

       В начальный момент t = 0 (при замыкании проводников) поток I_2а = 0. С течением времени поток I_2а увеличивается. разность потоков

D I₂ = I_2а - I_{2 b} = (R_2а dР_{2 b} - R_2b dР_2а)/(R_2аR_2b) – (1/R_2а + 1/R_2b) DР_2с (813)

идет на заряжание емкости К₂ ’ вторым зарядом, который заимствуется из емкости К₂ ”.

       Изменений фиктивной движущей силы d(DР_2с) складывается из изменений потенциалов dР_2с ’ и dР_2с ”.

                                           d(DР_2с) = dР_2с ’ - dР_2с ”.                                                      (814)

       Дифференциалы этих величин выражаются через емкости и количество dЕ₂ второго заряда, перенесенного за время dt, следующим образом:

                                           dЕ₂ = К₂ ’dР_2с’ = D I₂ dt;                                                     (815)

                                           dЕ₂ = - К₂ ”dР_2с” = D I₂ dt.                                                  (815)

       Из формул (814) и (815) получаем:

                                           d(DР_2с) = (1/К₂’ + 1/К₂”) DI₂dt.                                         (816)

       Связь между DР_2с и t находится из равенств (813) и (816) путем исключения D I₂ и интегрирования полученного уравнения:

       DР_2с = [(R_2а dР_{2 b} - R_2b dР_2а)/(R_2а + R_2b)]{1 – exp[-(1/R_2а + 1/R_2b)(1/К₂’ + 1/К₂”)t ]}. (817)

       В начальный момент (t = 0) фиктивная движущая сила равна нулю. С течением времени DР_2с растет по экспоненциальному закону. При t = ¥ наступает стационарный режим, величина DР_2с приобретает максимальное значение

                                           DР_{2с ¥} = (dР_{2 b} - m_2bа dР_2а)/(1 + m_2bа),                                (818)

где

                                           m_2bа = R_2b/R_2а.                                                                   (819)

       В условиях стационарного режима потоки второго заряда в проводниках а и b одинаковы:

                                           I_{2а ¥} = I_{2b ¥} = (dР_2а + DР_{2с ¥})/R_2а = (dР_2b - DР_{2с ¥})/R_2b =

                                           = (dР_2а + dР_2b)/(R_2а + R_2b) = dР₂/(R_2а + R_2b).                  (820)

       Как видим, фиктивная движущая сила зависит от частных движущих сил dР_2а и dР_2b и отношения сопротивлений проводников. При разных m_2bа она может принимать различные положительные и отрицательные значения. Величина DР_2с не есть движущая сила процесса циркуляции второго заряда, как иногда думают. Фактической движущей силой является разность dР₂.

 

       4. Частные случаи.

 

       Если один из проводников (а или b) разорвать, то поток второго заряда прекращается (I₂ = 0), линейная движущая сила пары становится равной ее контактной составляющей

                                           dР₂ = dР_2к = dР_{2 b} = - dР_2а = DР_{2с ¥ .}

       Если термодинамическая пара не имеет скачков потенциала dР_2а’ и dР_2а” (рис. 42), то [формула (810)]

                                           dР_2а = - dР_21а.

       Иногда можно пренебречь линейной составляющей движущей силы (dР₂₁ = 0). При этом

                                           dР₂ = dР_2к = dР_{2 b}.

       Фиктивная движущая сила в обобщенной паре не возникает, если отношение сопротивлений [формула (818)]

                                           m_2bа = dР_2b/ dР_2а.

       В частном случае, когда m_2bа ® 0, разность

                                           DР_{2с ¥} = dР_{2 b}.

       При m_2bа ® ¥ фиктивная движущая сила

                                           DР_{2с ¥} = - dР_2а.