
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напор и градиент потенциала.
1. Напор потенциала.
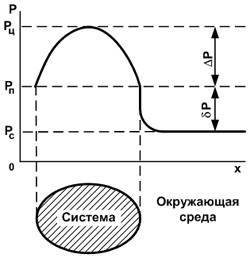
Для переноса существенны неоднородные поля заряда и потенциала. Эта неоднородность может быть вызвана различными причинами, о которых много говорится дальше. Одна из причин неоднородности может заключаться в том, что система и окружающая среда имеют разный состав материала. В этом случае кривая распределения потенциала имеет излом на контрольной поверхности, отделяющий систему от окружающей среды (рис. 2-а и 5).
Рис. 5. Схема определения перепада и напора потенциала.
Изучая свойства и поведение системы, часто можно подробно не вникать в свойства окружающей среды. Например, можно не интересоваться характером распределения потенциала в окружающей среде. Достаточно ограничиться лишь знанием общей разности потенциалов между поверхностью тела и окружающей средой вдали от тела. Эта разность называется напором потенциала и обозначается dР = Рс – Рп, (209) где Рс - значение потенциала окружающей среды вдали от системы, где не сказывается возмущающее действие тела на среду; Рп - значение потенциала на контрольной поверхности системы (рис. 5). Понятие напора потенциала на контрольной поверхности очень упрощает многие расчеты и определения.
2. Перепад потенциала.
При наличии неоднородного поля потенциала в теле общей характеристикой неоднородности может служить разность потенциалов DР = Рп – Рц, (210) где Рп - значение потенциала на поверхности; Рц - значение потенциала в центральной зоне тела. Эта разность называется перепадом потенциала в системе. Под перепадом обычно понимается максимальная разность потенциалов в сечении тела (рис. 5).
3. Градиент потенциала.
Если соединить все точки неоднородного поля, обладающие одинаковыми значениями потенциала, то получится поверхность уровня, или изопотенциальная поверхность. Движение вдоль изопотенциальной поверхности не сопровождается изменением потенциала. Переход с одной изопотенциальной поверхности на другую связан с изменением потенциала на величину DР. В общем случае такой переход обусловлен перемещением на расстояние D l. Скорость изменения потенциала на пути D l составляет
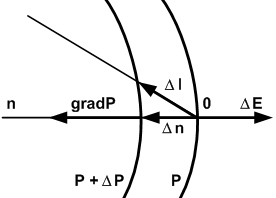
D Р/ D l. Наибольшая скорость изменения потенциала получается при перемещении вдоль направления нормали n к изопотенциальной поверхности (рис. 6). Эта скорость называется градиентом потенциала и обозначается через gradР, причем ½gradР ½ = lim ½ DР/ Dn ½ Dn ®0 = DР/ Dn. (211) По направлению градиент совпадает с нормалью, идущей в сторону возрастания потенциала. Если градиент потенциала не зависит от времен и координат у и z, то из выражения (211) в частном случае получается ½gradР ½ = dР/dх. (212) Градиент потенциала является чрезвычайно важной величиной, та как через него определяется количество перенесенного заряда и действующая на заряд сила.
4. Напряженность, или сила, поля.
В соответствии с основным постулатом заряд распространяется в сторону убывающего потенциала, т.е. градиент потенциала и поток заряда направлены в прямо противоположные стороны (рис. 6). Заряд перемещается под действием силы. Это говорит о том, что сила и поток заряда по направлению совпадают, а сила и градиент потенциала – нет. В связи с этим целесообразно ввести понятие напряженности, или силы, поля потенциала и определить это понятие следующим образом: G = - dР/dх. (213) Напряженность, или сила, поля по абсолютной величине равна, а по знаку противоположна градиенту потенциала. Ниже (гл. VI) строго доказывается, сто напряженность G представляет собой силу Рх, действующую на единицу заряда. Таким образом, показывается, что градиент потенциала является основной величиной, характеризующей процесс переноса зарядов. Здесь все эти понятия введены предварительно с тем, чтобы облегчить понимание закона переноса. Точнее говоря, перенос заряда происходит при наличии разности потенциалов. Поэтому в качестве движущей силы переноса могут служить напор, перепад и градиент потенциала. Но последний проще всего выражается через действующую силу.
Рис. 6. Схема определения градиента потенциала.
§ 34. Пятый главный закон движения (переноса).
1. Вывод обращенного дифференциального уравнения состояния.
Дифференциальное уравнение закона состояния выводится из обращенного уравнения состояния, которое записывается в несколько иной форме, чем это было рассмотрено в § 18. Например, при одной степени свободы (n = 1) общая связь между зарядом и потенциалом определяется формулой (102), а дифференциальная – формулой (103). Для вывода обращенного дифференциального уравнения состояния требуется выразить не потенциал через заряд, а, наоборот, заряд через потенциал. Имеем Е = f(Р); (214) dЕ = К dР, (215) где К – производное свойство движения третьего порядка [емкость, формула (128)]; К = 1/А = dЕ/ dР. Уравнения (214) и (215) являются обращенными по отношению к (102) и (103). При двух степенях (n = 2) свободы общие обращенные зависимости имеют вид: Е1 = f1(Р1; Р2); (216) Е2 = f2(Р1; Р2). (216) Эти зависимости получаются, если из второй строчки уравнений (105) найти заряд Е2 и подставить его в первую строчку, а величину Е1 подставить из первой строчки во вторую. Дифференцирование функций (216) дает dЕ1 = К11Р dР1 + К12Р dР2; (217) dЕ2 = К21Р dР1 + К22Р dР2, (217) где К11Р = (¶Е1/ ¶Р1)Р2; К22Р = (¶Е2/ ¶Р2)Р1; (218) К12Р = (¶Е1/ ¶Р2)Р1; К21Р = (¶Е2/ ¶Р1)Р2. (219) Наконец в общем случае n степеней свободы обращенное уравнение состояния имеет вид Е i = fi(Р1; Р2;...; Р n), (220) где i = 1, 2,..., n. После дифференцирования функции (220) получаем dЕi = где i = 1, 2,..., n. К iiР = ¶Е i/ ¶Р i; К rrР = ¶Е r/ ¶Р r; (222) К irР = ¶Е i/ ¶Р r; К riР = ¶Е r/ ¶Р i. (223)
Необходимо подчеркнуть, что в обращенные дифференциальные уравнения состояния второго порядка (17) и (221) входят емкости КР, найденные при постоянных значениях потенциалов (они обозначены индексом Р). Этим емкостям обратны коэффициенты АР, также взятые при постоянных Р: АР = 1/КР. (224) Коэффициенты АР в принципе отличны от коэффициентов А, входящих в обычные дифференциальные уравнения состояния (106) и (110). Неучет этого обстоятельства может привести к серьезным ошибкам, особенно если система находится вблизи абсолютного нуля потенциала. Разницы между емкостями К и КР (коэффициентами А и АР) нет только в том воображаемом случае, когда система располагает всего одной формой движения [уравнения (103), (128) и (215)]. Общие уравнения состояния (102), (105) и (109) написаны в соответствии с основным постулатом, согласно которому любое свойство движения есть однозначная функция зарядов. Обращенные уравнения (214), (216) и (220) вытекают из уравнений (102), (105) и (109). Однако отсюда вовсе не должно следовать, что потенциалы, являющиеся аргументами в уравнениях (214), (216) и (220), могут служить в качестве параметров состояния (первичных величин). Такая (кстати сказать, широко распространенная) точка зрения не соответствует реальному положению вещей. Фактически параметрами состояния (первичными величинами) являются только заряды. Справедливость функций (214), (216) и (220) есть следствие однозначности связи, существующей между зарядами и потенциалами. Но дальше этого роль потенциалов, как параметров состояния, не распространяется. В частности, потенциалы не обладают способностью перемещаться и т.д. Если бы уравнения (214), (216) и (220) могли служить основанием для того, чтобы рассматривать потенциалы как параметры состояния, тогда из обращенных уравнений состояния третьего и более высоких порядков можно было бы прийти к выводу, что параметрами состояния являются также коэффициенты А, В, С и D и т.д. Это явный абсурд.
2. Физический смысл обращенных уравнений.
Обращенные дифференциальные уравнения состояния (215), (217) и (221) связывают изменения зарядов с изменениями потенциалов. Но изменения зарядов происходят вследствие их переноса через контрольную поверхность. При этом для бесконечно малой системы изменение любого данного заряда в точности равно количеству заряда, переданного через контрольную поверхность. Следовательно, под dЕ в обращенных уравнениях можно понимать количество перенесенного заряда.
Изменение потенциала системы непосредственно связано с возникновением соответствующих разностей потенциалов, например, между системой и окружающей средой, либо между отдельными участками системы, если рассматривается процесс перераспределения заряда внутри системы, и т.д. Следовательно, под dР можно понимать некоторую разность потенциалов. Если вспомнить, что разность потенциалов служит движущей силой процесса переноса, сопряженного с потенциалом заряда, тогда физический смысл обращенных дифференциальных уравнений состояния проявляется очень четко. Обращенные дифференциальные уравнения состояния (215), (217) и (221) представляют собой обобщенные дифференциальные уравнения переноса, которые связывают количества переданных зарядов с имеющимися разностями потенциалов. Основные и перекрестные коэффициенты КР в обобщенных уравнениях переноса приобретают смысл обобщенных проводимостей системы.
3. Микроскопическая система.
Обобщенные дифференциальные уравнения переноса (215), (217) и (221) в наиболее общем виде выражают пятый главный закон (принцип) общей теории – закон переноса заряда. Согласно этому закону, количество перенесенного заряда складывается из n величин, каждая из которых пропорциональна соответствующей разности потенциалов, коэффициентами пропорциональности служат обобщенные проводимости КР. В законе переноса обращает на себя внимание действие простейшего принципа аддитивности: на количество перенесенного заряда влияют все n разностей потенциалов, причем влияние отдельных разностей суммируются. При этом соблюдается также принцип линейности: количество перенесенного заряда линейно (в первой степени) зависит от разностей потенциалов. Закон переноса, записанный в форме обобщенных уравнений, справедлив для любого уровня мироздания: макромира, микромира и т.д. В этих уравнениях такие заряды, как пространство и время, играют свою основную роль – объектов переноса. Это особенно важно для микромира, где рассматриваются процессы распространения квантов всех зарядов, включая метроны и хрононы. В условиях макромира обстановка существенно изменяется. Там пространство и время принято эксплуатировать только в качестве вспомогательных величин, а не объектов переноса. Поэтому макроскопические уравнения переноса в отличие от обобщенных не всегда можно применять для изучения свойств микромира. Упомянутая вспомогательная роль пространства и времени в макроскопических уравнениях сильно затрудняла правильное понимание физического существа этих зарядов.
4. Макроскопическая система.
Рассмотрим теперь макроскопическую модификацию обобщенного уравнения переноса. Будем называть ее общим (не смешивать с обобщенным) уравнением переноса. Для вывода общего уравнения необходимо ввести понятия потока и силы.
Естественно принять, что поток W заряда (или просто поток) пропрционален количеству перенесенного заряда: W = DdE, (225) где D - коэффициент пропорциональности. Формула (225) определяет количество заряда, переданного в определенных условиях. Эти условия конкретизируются путем соответствующего выбора коэффициента D. Термодинамическая сила, или просто сила, являющаяся движущей причиной переноса заряда, пропорциональна разности потенциалов: V = - CdP (226) где С - коэффициент пропорциональности. Коэффициент С характеризует конкретные условия переноса. В качестве силы V чаще всего служит напор или градиент потенциала. Этими величинами обычно ограничиваются потребности выбора коэффициента С для макроскопических явлений. Знак минус в правой части формулы (226) поставлен по следующей причине: для нашего мира условно принято, что заряд распространяется от большего потенциала к меньшему (§ 24). При этом величина dP является отрицательной [формула (157)]. Но поток заряда, а следовательно, и сила V должны быть положительными. Поэтому минус перед dP компенсирует отрицательное значение самой величины dP. С помощью установленных понятий потока и силы нетрудно вывести общие дифференциальные уравнения закона переноса. Например, в гипотетическом случае одной формы движения (n = 1) из выражений (215), (225) и (226) получаем W = ВV, (227) где В = - К(D/С). (228) Общее дифференциальное уравнение переноса (227) свидетельствует о том, что поток пропорционален силе. Коэффициент пропорциональности В представляет собой проводимость системы, он пропорционален ее емкости. Для двух степеней свободы системы (n = 2) из уравнений (217), (225) и (226) находим W1 = В11 V1 + В1 2 V2 (229) W2 = В21 V1 + В2 2 V2 (229) где W1 = DdE1; W2 = DdE2; (230) V1 = - CdP1; V2 = - CdP2; (231) B11 = - K11P(D/C); B22 = - K22P(D/C); (232) B12 = - K12P(D/C); B21 = - K21P(D/C). (233) Если система располагает n внутренними степенями свободы, то из выражений (221), (225) и (226) будем иметь Wi = где i = 1, 2,..., n; Bii = - KiiP(D/C); Brr = - KrrP(D/C); (235) Bir = - KirP(D/C); Bri = - KriP(D/C). (236) Общие дифференциальные уравнения переноса (227), (229) и (234) выражают прежний закон переноса, но форма их более удобна для изучения макроскопических явлений, чем форма обобщенных уравнений. Для использования общих уравнений надо придать конкретные значения коэффициентам пропорциональности С и D.
5. Частные формы макроскопических уравнений.
Посредством соответствующего выбора коэффициентов С и D можно получить большое множество различных выражений, определяющих потоки W и силы V. Для практических целей рекомендуется восемь основных вариантов выбора потоков и силы [4]. Из них ниже рассматриваются четыре наиболее употребительных. Удельный поток обобщенного заряда J, отнесенный к единице площади F контрольной поверхности и единице времени dt, определяется следующим образом: W = J; (237) где J = dE/(Fdt). (238) Сопоставление выражений (225) и (238) показывает, что для потока J, то коэффициент пропорциональности D = 1/(Fdt). (239) На практике широко употребляется также поток W = I; (240) где I = dE/dt, (241) который характеризует скорость переноса обобщенного заряда (в учении об электричестве величина I называется силой тока). Для этого потока коэффициент пропорциональности в формуле (225) D = 1/dt (242) Для обозначения конкретных потоков вместо W использованы новые буквы J и I. Это сделано с целью избежать возможной путаницы. В качестве термодинамической силы V обычно используются две величины - X и Y. Сила Х представляет собой напор интенсиала на контрольной поверхности системы: V = X; (243) Х = - dР, (244) что соответствует коэффициенту пропорциональности в формуле (226) С = 1. (245) Сила Y есть градиент потенциала V = Y; (246) Y = - dР/dх. (247) Выражение (247) получается из (226), если положить С = 1/dх. (248) Конкретным силам Х и Y также даны специальные буквенные обозначения, отличные от V. С помощью введенных потоков J и I и сил Х и Y общие дифференциальные уравнения переноса (227), (229) и (234) могут быть переписаны по-новому. При этом каждый из потоков J и I может сочетаться с каждой из сил Х и Y. Всего получается четыре частных варианта дифференциальных уравнений переноса. Для различного числа форм движения они выглядят следующим образом. В первом варианте сочетаются поток J и сила Х. При n = 1 из выражений (227), (228), (237), (239), (243) и (245) получаем J = aХ, (249) где a - коэффициент отдачи заряда на контрольной поверхности системы: a = - К(1/ Fdt). (250) В данном случае роль проводимости В играет величина a: В = a. (251) Аналогично при n = 2 из выражений (229) – (233) находим J1 = a 11 X1 + a 12 X2; (252) J2 = a 21 X1 + a 22 X2, (252) где a11 = - К11Р(1/ Fdt); a22 = - К22Р(1/ Fdt); (253) a12 = - К12Р(1/ Fdt); a21 = - К21Р(1/ Fdt); (254) При n степенях свободы общее уравнение (234) принимает вид Ji = где i = 1, 2,..., n; a ii = - КiiР(1/ Fdt); a rr = - КrrР(1/ Fdt); (256) a ir = - КirР(1/ Fdt); a ri = - КriР(1/ Fdt). (257) Во втором варианте сочетаются поток I и сила Х. При n = 1 уравнение (227) преобразуется к виду I = bХ, (258) где b - коэффициент отдачи заряда на контрольной поверхности системы: b = - К(1/ dt); (259) В = b. (260) При n = 2 из уравнений (229) находим I1 = b 11 X1 + b 12 X2; (261) I2 = b 21 X1 + b 22 X2, (261) где b11 = - К11Р(1/ dt); b22 = - К22Р(1/ dt); (262) b12 = - К12Р(1/ dt); b21 = - К21Р(1/ dt). (263) При n формах движения из формулы (234) получаем Ii = где i = 1, 2,..., n; b ii = - КiiР(1/ dt); b rr = - КrrР(1/ dt); (265) b ir = - КirР(1/ dt); b ri = - КriР(1/ dt). (266) В третьем варианте сочетаются поток J и сила Y. При n = 1 из общего уравнения (227) находим J = LY, (267) где L – проводимость системы по отношению к заряду: L = - К(1/F)(dx/ dt); (268) В = L. (267) При n = 2 из уравнений (229) имеем J1 = L11Y1 + L12Y2; (270) J2 = L21Y1 + L22Y2, (270) где L11 = - К11Р(1/F)(dx/ dt); L22 = - К22Р(1/F)(dx/ dt); (271) L1 2 = - К1 2Р(1/F)(dx/ dt); L2 1 = - К2 1Р(1/F)(dx/ dt). (272) При n степенях свободы общее уравнение (234) дает Ji = где i = 1, 2,..., n; Lii = - КiiР(1/F)(dx/ dt); Lrr = - КrrР(1/F)(dx/ dt); (274) Lir = - Кi rР(1/F)(dx/ dt); Lri = - Кr iР(1/F)(dx/ dt). (275) Наконец, в четвертом частном варианте сочетаются поток I и сила Y. При n = 1 получаем I = МY, (276) где М – проводимость системы по отношению к заряду:. М = - К(dx/dt); (277) В º М. (278) При n = 2 из уравнений (229) находим I1 = М11Y1 + М12Y2; (279) I2 = М21Y1 + М22Y2, (279) где М11 = - К11Р(dx/ dt); М22 = - К22Р(dx/ dt); (280) М12 = - К12Р(dx/ dt); М21 = - К21Р(dx/ dt). (281) В общем случае n степеней свободы уравнение (234) дает Ii = где i = 1, 2,..., n; Мii = - К iiР(dx/ dt); Мrr = - К rrР(dx/ dt); (283) Мir = - КirР(dx/ dt); Мri = - КriР(dx/ dt); (284) Напомним, что во всех перечисленных уравнениях переноса емкости берутся при постоянных потенциалах. Это замечание не касается только гипотетического случая, когда n = 1. Из конкретных дифференциальных уравнений переноса (255), (266), (273) и (282) видно, что в них координаты и время играют вспомогательную роль: относительно этих зарядов определяются потоки всех других. Такая постановка вопроса правомерна только для макроскопических тел и только в условиях, когда потоки пространства и времени отличаются стабильностью. При нестабильности процессов распространения пространства и времени вся картина переноса, определяемая упомянутыми уравнениями, резко усложняется. В этом случае целесообразно пользоваться обобщенными уравнениями переноса типа (215), (217) и (221). Заметная нестабильность условий возникает при значительном изменении зарядов системы, например, при изменении электрического и магнитного полей, гравитационного потенциала (если, например, система – космический корабль – приближается к звезде большой массы), количества движения (а следовательно, и скорости) и т.д. Уравнения (255), (266), (273) и (282) могут быть использованы при расчете микроскопических процессов, если частицы располагают большими запасами метронов и хрононов. Тогда по признаку пространства и времени частицы должны обладать континуальными (непрерывными) свойствами. Этим замечанием утверждается идея о том, что микроансамбли в принципе могут обладать по отношению к одним зарядам корпускулярными, а по отношению к другим – континуальными свойствами. Границы применимости рассмотренных частных уравнений для микромира могут быть установлены только тогда, когда станет известна величина метронов и хрононов и будут ясны заряды микрочастиц. Не исключено, что в отдельных случаях частные потоки зарядов будут более удобно относить не в пространству и времени, а к определенным другим зарядам, распространение которых в данных конкретных условиях отличается большей стабильностью, чем распространение пространства и времени. Все эти проблемы снимаются при использовании обобщенных уравнений переноса.
6. Связь между разноименными частными потоками и силами.
Сопоставление формул (237) и (241) показывает, что потоки J и I различаются только площадью F. Поэтому переход от одного потока к другому осуществляется с помощью соотношения I = FJ. (285) Аналогичная связь существует между разноименными частными проводимостями. Например, из выражений (249), (258) и (285) получаем b = F a. (286) Из формул (267), (276) и (285) находим М = FL. (287) Наконец, два последних равенства дают b /М = a /L. (288) Связь, существующая между силами Х и Y, определяется формулами (249) и (267), а также (258) и (276) aХ = LY; (289) bХ = МY. (290) Если считать, что величина перепада потенциаларавна величине напора, тогда формулы (289) и (290) преобразуются к виду (перепад и напор сокращаются) L = a Dхф; (291) М = b Dхф. (292) Эти равенства выражают правила, с помощью которых в уравнениях переноса можно переходить от одних сил (и проводимостей) к другим. Физический смысл размера Dхф определяется следующими соображениями.
Предположим, что имеется система Dх, проводимость которой равна L или М (рис. 7). На поверхности системы отдача заряда происходит с коэффициентами a или b. Если продолжить систему на расстояние Dхф (толщина так называемого фиктивного слоя), тогда явление отдачи заряда можно условно заменить явлением проводимости в фиктивном слое (заштрихован пунктиром), обладающим теми же коэффициентами проводимости, что и система. Правомерность такой замены обусловлена тем, что поток заряда, уходящий с поверхности системы вследствие явления отдачи, равен потоку заряда, теряемого системой через фиктивный слой посредством явления проводимости.
Рис. 7. Схема определения толщины фиктивного слоя.
Действительно, из формул (249) и (267), а также (258) и (276) получаем (рис. 7) J = a X = LY = - a DРф = - L(DРф/ Dхф) (293) I = b X = МY = - b DРф = - М(DРф/ Dхф) (294)
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.204.208 (0.161 с.) |
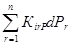 , (221)
, (221)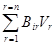 (234)
(234)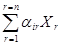 (255)
(255)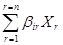 (264)
(264)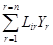 (273)
(273)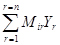 (282)
(282)



