
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о суммировании зарядов.
1. Дополнение к закону состояния.
Предположим, что имеется некоторый заряд Е i1, работающий в условиях стационарного режима и создающий первое поле. Независимо от него существует второй заряд Е i2 того же рода, создающий второе стационарное поле. В некоторый момент заряды Е i1 и Е i2 объединяются, образуя систему, изображенную на рис. 15. Требуется найти суммарное поле от системы зарядов. Задача заметно упрощается, если интересоваться только потоками нанозарядов, проходящих через некоторую контрольную поверхность F, охватывающую оба заряда.
Рис. 15. Схема системы, состоящей из двух зарядов.
Очевидно, что суммарный стационарный поток нанозаряда от системы не равен сумме потоков, образованных каждым из зарядов в отдельности. Это объясняется тем, что объединение зарядов в систему сопровождается появлением эффекта взаимного влияния, что изменяет действующие напоры потенциалов dРi1 и dРi2 и приводит к изменению величины потоков. Эффект взаимного влияния зарядов подчиняется общему закону состояния. Например, для двух зарядов (n = 2) применительно к i –той степени свободы уравнение состояния имеет вид dР i1 = Аi11dЕi1 + Аi12dЕi2; (387) dР i2 = Аi21dЕi1 + Аi22dЕi2, (387) Аi12 = Аi21. (388) Взаимное влияние зарядов определяется перекрестными коэффициентами Аi12 и Аi21, которые в соответствии с законом взаимности между собой равны. Благодаря существующему влиянию напоры dРi1 и dРi2 изменяются на величины dРi1 и dРi2, что, согласно формуле (368), изменяет потоки нанозаряда. Это значит, что отдельные (независимо действующие) заряды Еi1 и Еi2 в сумме излучают другое количество нанозаряда, чем система, состоящая из объединенных нарядов Еi1 и Еi2. Понять смысл полученного результата нетрудно, если вспомнить, что от характера взаимного расположения зарядов (расстояния r) зависит емкость системы и т.д. В случае системы, состоящей из k зарядов, уравнение состояния записывается следующим образом:
dРij = где j = 1, 2,..., k. А ijr = Airj. (390) Это уравнение в общем виде определяет взаимное влияние зарядов, а следовательно, и потоков нанозарядов внутри данной степени свободы i. При наличии нескольких степеней свободы приходится учитывать взаимное влияние как между одноименными, так и разноименными зарядами.
2. Содержание теоремы.
Предположим теперь, что взаимное влияние между зарядами отсутствует, т.е. перекрестные коэффициенты в уравнениях (387) – (390) обращаются в нуль. Тогда потенциал каждого из зарядов будет определяться только величиной самого заряда и напоры dРi не будут зависеть от расположения тел. В рассматриваемых гипотетических условиях излучение любого заряда не зависит от излучений всех остальных. Это значит, что суммарный поток нанозаряда от системы зарядов в точности равен алгебраической сумме потоков от отдельных зарядов. В этом состоит содержание теоремы о суммировании зарядов. Из теоремы следует, что если внутри замкнутой поверхности F содержится одинаковое число положительных и отрицательных зарядов, то суммарный поток нанозаряда через эту поверхность будет равен нулю. Аналогично, если внутри поверхности F вовсе нет зарядов, то суммарный поток полей также будет равен нулю (количество вошедшего нанозаряда равно количеству вышедшего). Разумеется, все это справедливо только в условиях стационарного режима и только когда соблюдаются равенства Аi12 = Аi21 = 0; (391) А ijr = Airj = 0. (391)
3. Теорема Остроградского-Гаусса.
Теорема о суммировании зарядов позволяет понять смысл и определить границы применимости известной теоремы Остроградского-Гаусса.
В электродинамике существуют понятия потоков напряженности и индукции электрического и магнитного полей. Напряженность и индукция определяются градиентами потенциалов [формулы (213) и (375)]. В свою очередь они определяют число силовых линий и линий индукции, исходящих из заряженного тела (заряда). Существует прямая пропорциональная связь между величинами электрических и магнитных зарядов и количествами силовых линий и линий индукции. Теорема Остроградского-Гаусса утверждает, что суммарное число линий, проходящих через замкнутую поверхность, охватывающую электрические и магнитные заряды, равно алгебраической сумме линий, выходящих из каждого заряда в отдельности. Заметим, что линии напряженности и индукции – это крайне формальные понятия, в течение длительного времени затруднявшие правильное понимание электрических и магнитных явлений. Вместе с тем эти понятия легко получить из общей теории, так как напряженность и индукция непосредственно связаны (пропорциональны) с потоком нанозаряда [формулы (369) и (370)], а сам поток – с величиной излучающего его макро- или микрозаряда [уравнения (367), (368), (387) и (389)]. Таким образом, из общей теории как частный случай вытекает теорема Остроградского-Гаусса. Она есть следствие теоремы о суммировании зарядов, справедливой только для стационарного режима и только в условиях, когда отсутствует взаимное влияние между зарядами. В реальных условиях теорема Остроградского-Гаусса неточно отражает действительность.
4. Принцип суперпозиции.
На основе изложенных соображений теперь можно дать оценку так называемому принципу суперпозиции. Этот принцип часто понимается как возможность суммировать (налагать) поля от различных источников. При этом суммарное поле от нескольких источников рассматривается как простая сумма полей, образуемых каждым из источников в отдельности. Никто никогда не доказывал справедливость этого принципа. Между тем его очень широко применяют для практических расчетов в самых различных областях знаний. Из предыдущего должно быть ясно, что принцип суперпозиции в общем случае дает неправильные результаты, так как не учитывает взаимного влияния источников полей. Точность этого принципа возрастает с уменьшением перекрестных коэффициентов в уравнениях (387) и (389).
Нестационарные поля.
1. Уравнение нестационарного переноса нанозаряда.
Рассмотренные выше закономерности (§ 41-43) были получены для стационарного режима распространения нанозарядов. В действительности поля чаще всего бывают нестационарными. В условиях нестационарного режима проявляются новые свойства полей и действуют несколько иные закономерности. В частности, неточно соблюдается теорема Остроградского-Гаусса. Это объясняется тем, что при нестационарных условиях количество испускаемого телами нанозаряда не равно количеству нанозаряда, проходящего через замкнутую поверхность F (рис. 15). Часть нанозаряда аккумулируется (или выделяется) объемом, ограниченным этой поверхностью. Причем погрешность, даваемая теоремой, тем выше, чем больше величина поверхности F и меньше скорость w распространения нанозарядов (полей).
Положение частично спасает то обстоятельство, что скорость распространения полей крайне велика, возможно, на много порядков выше скорости распространения фотонов (света). В результате на практике любое поле в течение ничтожных долей секунды оказывается хорошо развитым, вследствие чего эффект нестационарности ускользает от внимания. Нестационарный процесс распространения полей аналитически описывается общими уравнениями переноса типа (340), (345) и (349). В гипотетических условиях одной степени свободы (n = 1) из уравнений (340) и (343) имеем Uнан = LнанZ (392) или ¶ P/ ¶ t = Dнан(¶2P/ ¶x2), (393) где Dнан – диффузивность по отношению к нанозаряду (нанодиффузивность), Dнан = Lнан/(r cнан). (394) Здесь проводимость Lнан и удельная массовая емкость cнан также относятся к нанозаряду, величина r характеризует плотность среды. При двух степенях свободы (n = 2) уравнение (345) дает U1нан = L11нанZ1 + L12нанZ2; (395) U2нан = L21нанZ1 + L22нанZ2, (395) В общем случае n степеней свободы и трехмерного поля из уравнения (349) получаем Uiнан = где i = 1, 2,..., n. В уравнениях (395) и (396) основные коэффициенты характеризуют проводимость среды по отношению к данному нанозаряду, перекрестные – взаимное влияние потоков нанозарядов (полей).
2. Свойства уравнения.
Прежде всего следует обратить внимание на существование в наномире эффектов взаимного влияния полей. Количественная сторона этого влияния определяется величинами перекрестных коэффициентов Lirнан и Lriнан. Если Lirнан = Lriнан = 0, (397)
то поля распространяются независимо одно от другого. Строго говоря, условие (397) не соблюдается никогда. Однако в отдельных случаях допустимо пренебречь взаимным влиянием потоков нанозарядов и приближенно считать, что перекрестные коэффициенты проводимости равны нулю. Это сильно упрощает расчеты, так как вместо уравнения (396) можно пользоваться простейшим уравнением (392). Но вместе с тем имеются случаи, когда пренебречь взаимным влиянием потоков нельзя. В первую очередь это касается электрического и магнитного зарядов. Связь между ними проявляется крайне сильно, из-за этого до сих пор принято считать, что одно поле (магнитное) является производным от второго (электрического). Другая существенная особенность нестационарного уравнения переноса (396) заключается в том, что оно справедливо только для частного случая неподвижных зарядов. Если заряды, служащие источниками нанозарядов (полей), перемещаются, то задача сильно усложняется. Приходится принимать во внимание силовое взаимодействие зарядов и составлять более сложные общие уравнения, учитывающие характер движения самих зарядов. Простейшими уравнениями такого типа являются уравнения электродинамики Максвелла (§ 46).
§ 45. Методы определения наносвойств.
1. Постановка задачи.
Детальное изучение наномира следует начать с установления производных свойств третьего порядка – коэффициентов Анан, емкостей Кнан, проводимостей Lнан и т.д. В настоящее время известны только два относительные свойства наномира – проницаемости e Y (электрическая) и eмг (магнитная). Они характеризуют проводимость данного вещества по сравнению с проводимостью вакуума [формула (377)]. Для определения абсолютных значений наносвойств важно знать абсолютные количества нанозаряда, проходящего через определенные участки поля. Соответствующие определения можно сделать на основе использования полной совокупности уравнений главных законов общей теории и имеющихся экспериментальных данных по излучению в космосе. Однако при отсутствии абсолютных значений потоков нанозаряда также можно определить некоторые свойства наномира. Для этого полезно вспомнить идеи, которые существуют, например, в теории теплообмена для определения термофизических свойств различных материалов. При этом могут быть использованы уравнения переноса, приведенные в § 41 для стационарного режима, и нестационарные уравнения § 44.
2. Плоское поле.
Решение задачи о нестационарном распространении нанозаряда в бесконечном (неограниченном) пространстве (теле) от неограниченного плоского источника (заряда) находится путем интегрирования уравнения (393) при граничном условии первого рода (при постоянном потенциале Р0 на поверхности заряда). Соответствующее решение имеет вид [14] Р/Р0 = 1 – erf(u), (398)
где u = r/(2 В правую часть уравнения (398) входит хорошо известная функция ошибок Гаусса. Эта функция изменяется от 0 (при u = 0) до 1 (при u = ¥). Практически функция Гаусса близка к единице, когда аргумент u > 2,7.
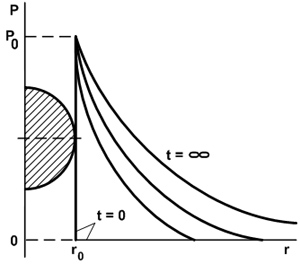
Из формулы (398) видно, что на поверхности заряда (r = 0) потенциал Р равен его начальному значению Р0. По мере насыщения пространства нанозарядом (с увеличением t) потенциал некоторой точки r возрастает (рис. 16). В пределе при t = ¥ пространство оказывается полностью насыщенным нанозарядом, все точки пространства приобретают значение потенциала, равное Р0.
Рис. 16. Распределение потенциала в сечении неограниченного тела в различные моменты (заряд – пластина).
3. Определение нанодиффузивности.
Решение (398) позволяет осуществить эксперимент по определению нанодиффузивности поля. Для этого надо иметь достаточно длинную и широкую пластину, заряженную до потенциала Р0. В момент t = 0 с пластины снимается экран и начинается излучение нанозаряда. Величина потенциала измеряется в момент t = t1 на расстоянии r1 от пластины (напротив ее центра). Расстояние r1 должно быть много меньше длины а и ширины в пластины. По найденному значению Р1 потенциала вычисляется отношение Р/Р0 и определяется функция Гаусса erf(u1) = 1 – (Р/Р0). (400) Этому значению функции соответствует аргумент u1 (определяется по таблицам) и диффузивность Dнан = r21/(4t1u21). (401) В этой расчетной формуле все величины известны. По ней с помощью экспериментальных данных вычисляется нанодиффузивность среды. Диффузивность включает в себя проводимость, плотность и емкость по отношению к нанозаряду – формула (394). Плотность находится легко. Что касается проводимости или емкости, то она может быть определена только в том случае, если известна абсолютная величина переданного нанозаряда. Для определения количества аккумулированного средой нанозаряда пригодна формула Енан = (2/ где bнан - коэффициент аккумуляции нанозаряда, bнан = F - поверхность излучения пластины, м2. К сожалению в эту формулу входят прежние неизвестные величины Lнан и cна н, поэтому таким способом найти количество нанозаряда нельзя.
4.Цилиндрические и сферические поля.
Интересные результаты можно получить на основе анализа процессов нестационарного распространения нанозаряда в неограниченной среде от цилиндрического и сферического источников. В данном случае в принципе невозможно полное насыщение среды до потенциала Р0 излучателя. Кривые распределения потенциала в среде с течением времени приближаются к некоторой предельной (стационарной) кривой, соответствующей значению t = ¥ (рис. 17 и 18). Вид предельной кривой может быть установлен путем интегрирования уравнения (393) [20]. Еще проще ее можно найти из соотношений (381) – (383), характеризующих закон изменения градиента потенциала с координатой в условиях стационарного режима. Очевидно, стационарному режиму должен отвечать постоянный поток нанозаряда, проходящий через любое сечение r среды. В частности, для плоского источника, когда площадь F не зависит от координаты r, такие условия возникают только при dР /dх = (dР /dх)0 = 0, (404) что на рис. 16 соответствует горизонтальной прямой Р = Р0, (405) нулевому потоку и полному насыщению пространства нанозарядом.
Рис. 17. Распределение потенциала в сечении неограниченного тела в различные моменты r (заряд – бесконечно длинный круглый цилиндр).
Рис. 18. Распределение потенциала в сечении неограниченного тела в различные моменты r (заряд – шар).
Для цилиндрического источника интегрирование уравнения (382) с разделяющимися переменными (х º r) дает Р = Р0 - (dР /dх)0 r0ln(r/r0). (406) При r = r0 потенциал среды Р = Р0. С увеличением расстояния r стационарное значение потенциала убывает по логарифмическому закону. Градиент потенциала в формуле (406) можно выразить через поток нанозаряда. В соответствии с равенствами (370) и (382) имеем dЕ нан = - Lнан (dР /dх)0(r0/r)2 p rldt, где l - длина цилиндра, м. Следовательно, Р = Р0 - (Jнан/Lнан) r0ln(r/r0), (407) где Jнан = dЕнан/(F0dt); F0 = 2 p r0l. Предельная (стационарная) кривая для сферического источника находится путем интегрирования уравнения (383). Получаем Р = Р0 - (dР /dх)0 r20[(1/r0) - (1/r)]. (408) Исключим отсюда градиент потенциала с помощью выражения dЕ нан = - Lнан (dР /dх)0(r20/r2)4 p r2dt, которое найдено из формул (370) и (383). Окончательно имеем Р = Р0 - (Jнан/Lнан) r20[(1/r0) - (1/r)] = Р0 – [(Jнан/(4 p Lнан) ][(1/r0) - (1/r)]. (409) где Jнан = dЕнан/(F0dt); Iнан = dЕнан/ dt; F0 = 4 p r20. Соответствующие предельные кривые (405), (407) и (409) для плоского, цилиндрического и сферического полей изображены на рис. 19.
Рис. 19. Относительное расположение предельных кривых распределения потенциала для плоского (1), цилиндрического (2) и сферического (3) зарядов. Формулы (407) и (409) связывают нанопроводимость с полем потенциала, поэтому их можно было бы использовать для экспериментального определения нанопроводимости среды. Однако для этого надо знать величину потока нанозаряда. Анализ полученных уравнений распространения нанозарядов позволяет сделать много важных выводов. Прежде всего отметим, что известно бесчисленное множество измерений потенциалов различных плоских, цилиндрических, сферических полей (именно такие задачи были рассмотрены выше). Но ни один экспериментатор никогда не наблюдал изменения какого-либо потенциала со временем, т.е. не замечал эффекта нестационарности. Во всех случаях поле потенциала было стационарным, соответствующим предельным кривым, изображенным на рис. 19. Согласно дифференциальному уравнению (393), это должно свидетельствовать о крайне высоких значениях нанодиффузивности среды. Только при этом условии скорость изменения потенциала со временем будет достаточно большой. Большие диффузивности получаются при высоких значениях проводимости и малых – емкости [формула (394)]. При этом большие проводимости обусловлены наличием крайне высоких скоростей распространения нанозаряда. Именно такими свойствами по отношению к нанозаряду обладают различные среды, в том числе вакуум. Благодаря очень большим нанодиффузивностям потенциал быстро принимает предельные значения, определяемые уравнениями (405), (407) и (409). Этим обстоятельством объясняются имеющиеся экспериментальные данные по измерению потенциалов полей. Необходимо, однако, отметить, что хотя скорость распространения нанозаряда очень велика, она все же не равна бесконечности. Кроме того, согласно уравнениям нестационарного переноса, приближение поля к стационарному состоянию происходит с конечной скоростью, которая асимптотически (при t ® ¥) стремится к нулю. Следовательно, в принципе возможно уловить в опыте изменения потенциала перед тем, как он достигнет предельной кривой на рис. 19. Именно эта идея положена в основу рассмотренного выше метода определения нанодиффузивности с помощью плоского поля. Аналогичные определения можно сделать также с помощью цилиндрических и сферических полей. Однако при этом расчетные формулы имеют более громоздкий вид. Что касается возможностей экспериментального обнаружения изменений потенциала, то для этого, по-видимому, придется пользоваться крайне точными измерительными приборами с высокой разрешающей способностью, позволяющими фиксировать изменения потенциала за ничтожно малые отрезки времени. При постановке экспериментов следует не упускать из виду принцип стабильности и связанные с ним идеи. Например, длина и ширина пластины и длина цилиндра в опытах должны быть много больше расстояния r, на котором измеряется потенциал. С уменьшением размеров тел начинает сказываться искажающее влияние их границ. При очень больших расстояниях r по сравнению с размерами тела эти размеры, наоборот, перестают влиять на результаты, так как пластина и цилиндр образуют практически одинаковые сферические поля. Таким образом, в отношении конфигурации лучше всего пользоваться шаровым зарядом, у которого нет границ и поэтому не приходится думать о возможности искажения поля. В свою очередь у плоского поля наблюдается наименьшая скорость приближения потенциала к стационарному значению. Это облегчает измерения. Но возникают дополнительные трудности, связанные с осуществлением плоского заряда большой длины и ширины. В заключении отметим, что факт существования слишком кратковременного периода нестационарного развития поля сильно повлиял на наши представления о свойствах наномира и на характер того теоретического аппарата, с помощью которого эти свойства изучаются. В частности, этот факт привел к тому, что нестационарный период обычно во внимание не принимается. Отсюда возникла крайне формальная идея о возможности оценки свойств известных полей (электрического и магнитного) с помощью таких понятий, как напряженность и индукция. По существу напряженность и индукция – это градиент потенциала. В результате родились весьма странные представления о существовании потоков градиента потенциала (напряженности и индукции). Все это роковым образом сказалось на понимании электрических и магнитных, а за ними и всех остальных явлений. Следствием этого явилась невозможность правильной оценки границ применимости теоремы Остроградского-Гаусса и уравнений электродинамики Максвелла, на которых основывается теория относительности Эйнштейна.
Уравнения Максвелла.
1. Общий вид уравнений.
Максвелл обобщил известные в его время законы Кулона, Био-Савара, Ампера и т.д. и открытое Фарадеем явление электромагнитной индукции. Уравнения Максвелла, записанные в векторной форме, имеют следующий вид [7]: divH Y = 4 p r Y; (410) divHмг = 0; (411) rotG Y = - (1/c)(¶ Нмг/ ¶ t); (412) rotGмг = (1/c)(¶ Н Y / ¶ t) + (4 p/с) J Y; (413) Н Y = e Y G Y; (414) Н мг = e мг Gмг; (415) J Y = L Y (G Y + G Yстор), (416) где с – скорость света; r Y - плотность пространственно распределенного электрического заряда. Символ div означает операцию взятия дивергенции, а rot - ротора в векторном анализе. Остальные обозначения прежние. Основное уравнение (410) обобщает уравнение Кулона, (411) – идею об отсутствии в природе магнитных зарядов, аналогичных электрическим, (412) – закон электромагнитной индукции Фарадея, (413) – опытные факты об источниках вихрей магнитного поля. Дополнительные уравнения (414) и (415) суть частные формы общего выражения (380), формула (416) определяет поток электрического заряда с учетом действия сторонних сил (G Yстор). Из формул (410) – (416) видно, что они основываются на рассмотренных ранее понятиях напряженности и индукции электрического и магнитных полей. Уравнения Максвелла несимметричны относительно электрической и магнитной степеней свободы. Это обусловлено тем, что по Максвеллу не существует магнитных зарядов, подобных электрическим. Однако уравнения не исключают возможности включения в них свободных магнитных зарядов и соответствующих потоков. При этом не возникает никаких противоречий [7]. В симметричной записи формулы (411) и (412) приобретают вид divHмг = 4 p rмг; (417) rotGмг = - [(1/c)(¶ Нмг/ ¶ t) + (4 p/с) Jмг ]. (418) Кроме того, добавляется уравнение для потока магнитного заряда Jмг = Lмг(Gмг + Gмг.стор). (419) Уравнения Максвелла обратимы (симметричны) относительно направления течения времени: они допускают замену t на -t. Исключение составляет уравнение (416) закона Ома, которое необратимо, ибо при распространении электрического заряда выделяется джоулева теплота, вызванная наличием эффекта диссипации (трения). Формулы (410) – (416) представляют собой наиболее полную известную в настоящее время совокупность уравнений, которые описывают электромагнитные взаимодействия с учетом потока J Y электрического заряда, образующего поле.
2. Вывод уравнений.
Лучше всего понять смысл и оценить границы применимости уравнений Максвелла можно только в том случае, если вывести их методами единой теории и показать, частным случаем каких более общих уравнений они являются. С целью вывода уравнений Максвелла воспользуемся рассуждениями, которые привели к нестационарному уравнению (393) простейшего типа (n = 1). Для начала введем в уравнение (393) пространственно распределенный источник нанозаряда qнан = dЕнан/(dVdt). (420) Это количество нанозаряда выделяется (или поглощается) в 1 м3 за 1 секунду. В объеме dV за время dt выделяется (или поглощается) нанозаряд в количестве dЕнан = qнанdVdt. Эту величину надо вычесть из заряда, определяемого формулой типа (338). В результате из выражений типа (337) и (338) получается следующее уравнение нестационарного переноса с учетом действия источника (n = 1): ¶Р/ ¶ t = Dнан [(¶ 2Р/ ¶ х2) + (qнан/ r cнан)]. (421) Это уравнение отличается от прежнего (393) дополнительным слагаемым в правой части. Если имеется несколько (k) источников (зарядов), то их взаимное влияние учитывается с помощью уравнений состояния типа (389). В случае нескольких (n) степеней свободы приходится пользоваться общими уравнениями нестационарного переноса типа (396). При этом взаимное влияние разнородных источников (зарядов) учитывается уравнениями состояния типа (110), а одноименных – типа (389). Однако для простоты рассуждений не будем выписывать более общих (громоздких) уравнений, а ограничимся рассмотрением только одной степени свободы (n = 1) и одного источника (k = 1). Выведем теперь уравнение (421) с использованием преобразования Остроградского. Через замкнутую поверхность F, ограничивающую объем V, за единицу времени проходит заряд
Знак (F) означает, что интеграл берется по всей поверхности F. При наличии пространственно распределенного источника заряда в объеме V за единицу времени выделяется (или поглощается) заряд Эти интегралы берутся по всему объему V. Согласно закону сохранения заряда, два последних выражения между собой равны, т.е.
В соответствии с преобразованием Остроградского имеем В результате предыдущее равенство преобразуется к виду Отсюда находим r cнан (¶ Р/ ¶ t) = div(LнанgradP) + qнан. (422) У идеальных тел проводимость Lнан есть величина постоянная, поэтому уравнение (422) можно окончательно записать так: ¶ Р/ ¶ t = Dнанdiv(gradP) + qнан/(r cнан). (423) В условиях одномерного поля это уравнение в точности совпадает с прежним уравнением (421). Предположим далее, что поле нанозаряда не обладает собственной нестационарностью, оно целиком привязано к источнику (заряду). Тогда придется положить ¶Р/ ¶t = 0. (424) Будем также считать, что нанозаряд распространяется в вакууме. При этом gradP = - Н, (425) где Н – индукция поля. В результате уравнение (423) приобретает вид divН = qнан/ Lнан. (426) Применительно к электрической степени свободы отсюда получаем
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 82; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.66.31 (0.175 с.) |

 , (389)
, (389) , (396)
, (396) ), (399)
), (399)
 )bнанР0F
)bнанР0F  , (402)
, (402) , (403)
, (403)

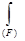 LнанgradPdF.
LнанgradPdF.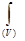 r cнан (¶ Р/ ¶ t)dV -
r cнан (¶ Р/ ¶ t)dV - 


