Глава VIII . Разделение движения.

 

 

Эффект разделения.

 

Характеристика новой формы движения.

 

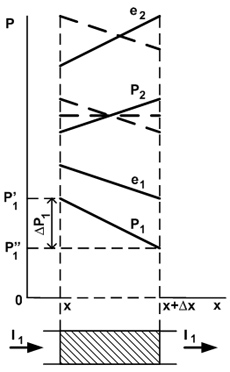
       Согласно принципу притяжения и отталкивания, природе присуще одновременно две прямо противоположные тенденции – к установления равновесия путем рассредоточения движения (благодаря силам отталкивания) и к нарушению равновесия – путем концентрации движения (благодаря силам притяжения). Такое единство противоположностей сопровождает эволюцию движения на всех ее этапах. В частности, перенос движения, ведущий к установлению равновесия, всегда сопровождается эффектом разделения, т.е. созданием дополнительной разности концентраций движения. Суть этого эффекта легко пояснить на примере системы с n > 1, в которой имеется поток какого-либо одного заряда.

       Если к системе приложена некоторая разность потенциалов DР₁ (рис. 32), то под ее действием происходит перенос первого заряда, а также перераспределение всех остальных. Соответствующие заряды на рис. 32 обозначены маленькими буквами, они отнесены к единице объема системы:

                                           е = Е/ V,                                                                             (617)

 

                               Рис. 32. Схема распределения удельных

зарядов и потенциалов вдоль проводника

с потоком первого заряда.

 

 

т.е. величина е представляет собой объемную концентрацию заряда. Второй потенциал может принять одно из распределений, отмеченных цифрами 1, 2 и 3.

       Неравномерное распределение концентрации второго заряда под действием разности первого потенциала есть концентрационный эффект, или эффект разделения.

 

       2. Расчетные формулы.

 

       Количественная сторона концентрационного эффекта может быть установлена, например, с помощью уравнения состояния (106). Продифференцируем его по х в предположении, что коэффициенты а постоянны (используем удельные величины, отнесенные к единице объема):

                                           dР₁/dх = а₁₁(dе₁/dх) + а₁₂(dе₂/dх);                                   (618)

                                           dР₂/dх = а₂₁(dе₁/dх) + а₂₂(dе₂/dх).                                    (618)

       В этих уравнениях градиент первого потенциала и градиент концентрации первого заряда не равны нулю. Поэтому в общем случае не равны нулю также градиент второго потенциала и градиент концентрации второго заряда. Как правило, градиент концентрации второго заряда направлен в сторону, противоположную градиентам первых потенциала и заряда (сплошная линия 3 на рис. 32). Это легко видеть на примере частного случая, когда можно пренебречь градиентом второго потенциала (dР₂/dх = 0). При этом из уравнения (618) получаются следующие простейшие линейные зависимости между всеми градиентами:

dе₂/dх = - (а₂₁/а₂₂)(dе₁/dх);                                                (619)

dР₁/dх = [(а₁₁а₂₂ – а₁₂а₂₁)/а₂₂](dе₁/dх).                              (620)

       Знак минус в уравнении (619) указывает на то, что градиенты концентрации первого и второго зарядов направлены в противоположные стороны, т.е. убывание вдоль проводника концентрации первого заряда приводит к возрастанию концентрации второго заряда. Иными словами, так, где первый потенциал имеет большее значение, концентрация второго заряда меньше и наоборот.

       Разность концентраций второго заряда на концах проводника обозначим через

                                           DС₂ = е₂ ^” – е₂ ’.                                                                   (621)

       Тогда суммарный эффект разделения второго заряда под действием разности DР₁ первого потенциала определится с помощью так называемого коэффициента разделения

                                           k_рд = DС₂/ DР₁.                                                                   (622)

       В частном случае вторым зарядом может служить масса.

 

 

Примеры эффектов.

 

Эффект Соре.

 

       В 1856 г. Людвиг обнаружил разность концентраций в пробах раствора, которые были взяты из участков сосуда с различными температурами. Позднее (1879-1881 гг.) Соре более подробно исследовал этот эффект, который с тех пор получил наименование эффекта Соре (термическая диффузия). Суть эффекта Соре заключается в том, что в растворе при наличии градиента температуры возникает градиент концентрации растворенного вещества. Концентрация вещества возрастает в направлении убывании температуры. Как видим, этот опытный факт находится в полном соответствии с выводами общей теории.

       Для увеличения эффекта разделения прибегают к повторному разделению обогащенной смеси.

       На практике широкое применение находит метод разделения газов, в том числе изотопов, под действием разности температур (термическая диффузия). Особенно эффективны в этом отношении колонки Клаузиуса и Диккеля, в которых разделение ускоряется конвективными токами газа. Таким способом можно добиться почти полного разделения смеси.

 

       2. Эффект Дюфора.

 

       Эффект Дюфора также связан с явлениями диффузии. Он обратен по отношению к эффекту Соре. В общем случае эффект, обратный данному, получается, если в явлении поток, сопряженный с первой внутренней степенью свободы системы, заменяется потоком, сопряженным со второй внутренней степенью свободы.

       В 1873 г. Дюфор показал, что диффузия одного газа в другой (наличие градиента концентрации массы) приводит к возникновению градиента температуры, хотя оба газа первоначально имеют одинаковую температуру (в эффекте Соре градиент температуры вызывает возникновение градиента концентрации массы).

       Необходимо отметить, что в эффекте Дюфора правильно говорить не о градиенте концентрации массы, а о градиенте диффузионного потенциала m_дф, ибо движущей силой диффузии является не концентрация, а величина m_дф (§ 10). Таким образом, в эффекте Дюфора градиент диффузионного (первого) потенциала вызывает появление градиента концентрации термического (второго) заряда. При этом градиент температуры (второй потенциал) не равен нулю (в эффекте Соре вторым является диффузионный потенциал, градиент которого в общем случае также не равен нулю).

 

       3. Прочие эффекты.

 

       Всего существует бесчисленное множество концентрационных эффектов. Все они подчиняются главным законам общей теории.

       Например, в известном явлении Хитторфа под действием градиента электрического потенциала возникает градиент концентрации вещества.

       Автору удалось наблюдать эффект возникновения градиента концентрации электрического заряда под действием градиента температуры в металлах [4, 5].

       Еще проще наблюдать в газе появление градиента концентрации массы под действием градиента температуры [5] и т.д.