
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точка пересечения двух прямыхСодержание книги
Поиск на нашем сайте
Пусть прямые l 1: A 1 x + B 1 y + C 1 = 0 и l 2: A 2 x + B 2 y + + C 2 = 0. пересекаются. Требуется найти точку точку пересечения этих прямых. Для этого достаточно решить систему двух уравнений с двумя неизвестными x и y:
Пример. Найти точку пересечения прямых l 1: 2 x + +3 y – 2 = 0 и l 2: x – y + 4 = 0. Решение: Запишем систему (1.6.10) и решим ее
Ответ: M (–2, 2).
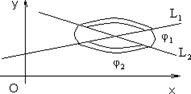
Угол между двумя пересекающимися прямыми Пусть прямые l 1: y = k 1 x + b 1 и l 2: y = k 2 x + b 2 пересекаются. Углом j между двумя пересекающимися прямыми называется наименьший из углов j1 и j2.
Рис. 1.6.25
Пример. Найти угол между прямыми y = 2 x – 4 и y = –3 x + 1. Решение: Найдем угловые коэффициенты этих прямых: k 1 = 2, k 2 = –3. (см.
tgj = = = 1. Отсюда j = 45º.
Ответ: j = 45º. Пример. Найти угол между прямыми 2 x + 4 y + 5 = 0 и x + 2 y – 3 = 0.
Решение: По формуле (1.6.5) найдем угловые коэффициенты прямых: k 1 = – 2/4 = – 1/2; k 2 = – 1/2. Применяем формулу (1.6.10):
tgj =
= 0. Отсюда j = 0º. Прямые параллельны.
Ответ: j = 0º.
Пример. Найти угол между прямыми 2 x + 3 y – 2 = 0 и x – y + 4 = 0. Решение: По формуле (1.6.5) найдем угловые коэффициенты: k 1 = – 2/3, k 2 = –1/(–1) = 1.
Применим формулу (1.6.11) tg j = 3 - = 3 = 5, отсюда j = arctg 5.
Ответ: j = arctg 5. 1 + 1(- 23) 1
Пример. Найти угол между прямыми 3 x + 5 y + 1 = 0 и 5 x – 3 y – – 2 = 0.
Решение: Находим угловые коэффициенты прямых: k 1 = – 3/5, k 2 = – 5/(–3) = 5/3. По формуле (1.6.11) имеем
tg j = 3 5 = 15 . Тангенс угла j не существует, следовательно, угол
5 3 j = 90º. Прямые взаимно перпендикулярны.
Ответ: j = 90º.
Условие параллельности двух прямых
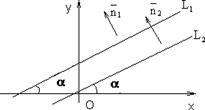
Рис. 1.6.26 Пусть даны две прямые l 1: y = k 1 x + b 1 и l 2: y = k 2 x + b 2. Так как прямые параллельны, то они имеют одинаковый угол наклона α с осью Ox и, следовательно, одинаковые угловые коэффициенты: k 1 = = k 2.
(1.6.11) получим tgj = = 0. Отсюда k 1 – k 2 = 0,
Таким образом, условием параллельности прямых является равенство их угловых коэффициентов.
Пример. Определить, какая из двух прямых l 1: 2 x + y – 7 = 0 или l 2: 4 x – 2 y + 1 = 0 – параллельна третьей прямой l 3: 4 x + 2 y + 3 = 0. Решение: По формуле (1.6.5) находим угловые коэффициенты каждой прямой. k = - 2 = – 2;
2 -2 = 2; k 3 = - 4 = -2.
Имеем: k 1 = k 3, следовательно, l 1 || l 3 (по 1.6.12).
Ответ: l 1 || l 3. В том случае, когда параллельные прямые заданы общими уравнениями, можно использовать геометрический смысл коэффициентов А и В. Напомним, что в уравнении Ax + By + C = 0 числа А и В определяют
решение приведенного выше примера. Решение: Две прямые будут параллельны, если их нормальные векторы будут коллинеарны. Выпишем нормальные векторы данных прямых:` n 1 = (2, 1), ` n 2 = (4, –2). ` n 3 = (4, 2). Проверим пропорциональность координат: 2 ¹ 1;
4 ¹ - 2;
2 = 1. Координаты векторов` n 1 и` n 3
4 - 2 4 2 4 2 пропорциональны, то есть ` n 1 ||` n 3. Следовательно, прямые l 1 || l 3.
Ответ: l 1 || l 3.
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 140; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.149.167 (0.007 с.) |

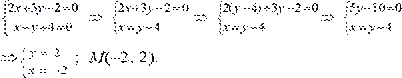

 Формула для нахождения угла j между прямыми имеет вид:
Формула для нахождения угла j между прямыми имеет вид:
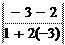
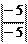 1.6.1). По формуле (1.6.11) получим
1.6.1). По формуле (1.6.11) получим
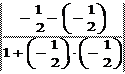
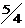 = 0
= 0

 3
3
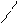
 5 - (- 3 ) 34
5 - (- 3 ) 34

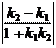 Эту же формулу можно получить и другим способом. Угол между параллельными прямыми равен 0º, т.е. j = 0º, tgj = tg0º = 0. Из формулы
Эту же формулу можно получить и другим способом. Угол между параллельными прямыми равен 0º, т.е. j = 0º, tgj = tg0º = 0. Из формулы 1 1
1 1 k = - 4
k = - 4 2
2 координаты нормального вектора n = (A, B). Поэтому рассмотрим другое
координаты нормального вектора n = (A, B). Поэтому рассмотрим другое





