Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные элементарные функции. Элементарные функции
Основные элементарные функции Основными элементарными функциями называются следующие: y = x a (
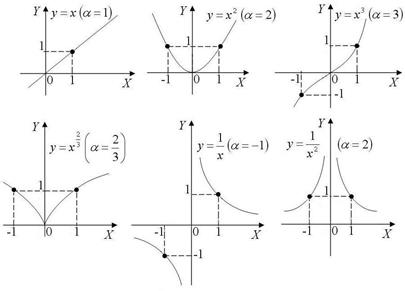
a - любое действительное число) - степенная функция. При различных a графики этой функции будут различны, на рис. 8 приведены графики степенной функции при некоторых значениях показателя a .
Функция
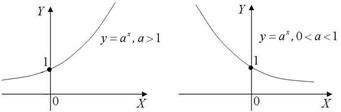
y = a x
(a > 0, a ¹ 1) Рис. 8 - показательная функция, ее графики приведены на рис. 9. Мы видим, что при a >1 функция y = a x является возрастающей, а при 0 < a < 1 - убывающей;
Функция
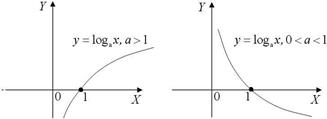
y = loga x
(a > 0, a ¹ 1) Рис. 9 - логарифмическая функция, ее графики при различных значениях основания a приведены на рис. 10. При a >1 логарифмическая функция возрастает, при 0 < a < 1 - убывает (рис.10).
Рис. 10 Далее следуют тригонометрические функции y = sin x,
y = cos x,
Функция y = sin x, ограниченная (sin x £ 1), нечетная функция с периодом l = 2 p (рис. 11).
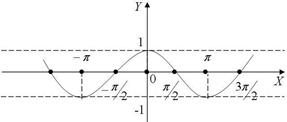
Функция y = cos x, ограниченная ( cos x £ 1), четная функция с периодом l = 2 p (рис. 12).
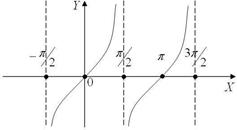
Функция Рис. 12 y = tg x, периодическая функция с периодом
l = p
(рис. 13).
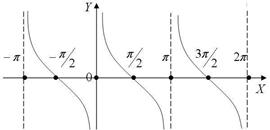
Функция Рис. 13 y = ctg x, периодическая функция с периодом
l = p
(рис. 14).
Рис. 14 Обратные тригонометрические функции y = arcctg x
y = arcsin x,
y = arccos x,
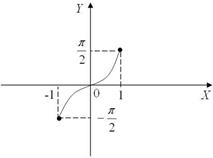
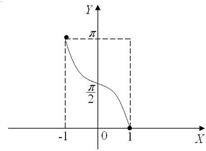
y = arctg x, Функция y = arcsin x. Область определения этой функции отрезок [-1;1], множество значений – отрезок é- p ; p ù . Ее график приведен на рис. 15. ëê 2 2 úû
Рис. 15 Функция y = arccos x. Область определения функции y = arccos x - отрезок
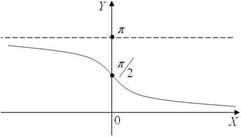
[-1, 1], множество значений – отрезок [0, p ]. График этой функции приведен на рис. 16. Рис. 16 Функция y = arctg x. Область определения этой функции вся числовая ось (- ¥; + ¥), множество значений – открытый интервал æ- p ; p ö , график
функции
y = arctg x ç ÷
приведен на рис. 17.
Рис. 17 Функция y = arcctg x. Область определения этой функции вся числовая ось (- ¥; + ¥), множество значений – открытый интервал (0; p), график функции y = arcctg x приведен на рис. 18.
Рис. 18 Элементарные функции Функции, полученные из основных элементарных функций с помощью конечного числа арифметических операций и конечного числа операций взятия функции от функции, называются элементарными.
Всякая элементарная функция может быть задана одной формулой на всей области своего определения. Например,
3 x 2 + x
, y = sin 3 æ x ö - 5 × 2- x 2
По сути дела, любая функция, закон соответствия которой задан одной формулой, является для нас элементарной, пока мы не овладеем другими знаками записи формул, кроме знаков арифметически операций и символов, которыми обозначаются основные элементарные функции.
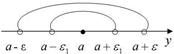
Предел функции. Понятие о сходимости числовой Последовательности. Предел переменной величины. Из разнообразных способов поведения переменных величин наиболее важен такой, при котором переменная величина стремится к некоторому пределу. В этом случае значения, принимаемые переменной величиной y, становятся сколь угодно близкими к некоторому постоянному числу a - пределу этой переменной величины. Определение предела имеет простой геометрический смысл: неравенство
интервале (a - e, a + e) (рис. 19). Таким образом, можно дать определение предела переменной величины в геометрической форме. Число a называется пределом переменной величины y, если для любой (сколь угодно малой) e - окрестности точки a можно указать такой момент в изменении переменной y, начиная с которого все ее значения попадают в e - окрестности точки a (рис. 19 и 20).
Записывается это следующим образом a = lim y (lim - первые буквы слова limes - предел) или y ® a. Процесс приближения к пределу необходимо понимать в динамике: взяли некоторую e - окрестность точки a, начиная с некоторого момента все значения переменной y попадают в эту окрестность; теперь возьмем e 1 < e , начиная с некоторого (более отдаленного) момента все значения переменной
y попадают в e 1 т.д. (рис. 20). - окрестность (меньшую по сравнению с первой) точки a и Однако, в определении предела осталась нерасшифрованной весьма существенная фраза: «начиная с некоторого момента в процессе изменения переменной величины y».
Предел функции при x ® ¥ . Пусть функция y = f (x) задана на интервале (p; + ¥). Определение. Число a называется пределом функции f (x) При x ® +¥, если для любого сколь угодно малого положительного числа e найдется такое число N, зависящее от e (N = N (e)), что для всех x > N выполняется
Здесь переменная, стремящаяся к пределу, это функция f (x); оставшаяся нерасшифрованной в общем определении предела переменной фраза «начиная с некоторого момента» в этом случае расшифровывается как «для всех x, больших некоторого N». Применяемое в этом случае обозначение предела таково: lim x ®+¥ f (x) = a. Геометрически тот факт, что a = lim x ®+¥ f (x) означает следующее (рис. 21). Возьмем произвольное e > 0 и на оси ординат, на которой откладываются значения функции при построении графика, построим e - окрестность точки a; через концы интервала (a - e, a + e) проведем горизонтальные прямые y = a - e и y = a + e. Между этими прямыми образуется полоса, которую называют e - полосой вокруг прямой y = a. Смотрим, когда границы e - полосы при движении вправо в последний раз пересекут график функции, эту точку спроектируем на ось абсцисс и получим искомое N. При всех x > N
Рис. 21 Аналогично тому, как был определен
lim x ®+¥
f (x), определяются пределы lim x ®-¥ f (x) и lim x ®¥ f (x). В последнем случае предполагается, что x ® +¥ и x ® -¥ .
Предел функции при x ® x 0 (предел функции в точке). Дадим определение предела функции при x стремящемся к конечному значению x 0. Будем считать, что функция y = f (x) определена во всех точках некоторого интервала (a, b), содержащего точку x 0, кроме, быть может, самой точки x 0. Если при неограниченном приближении точки x к точке x 0 значения функции f (x) неограниченно приближаются к некоторому числу a, то говорят, что число a является пределом функции f (x) при x стремящемся к x 0 (x ® x 0 ). В этом случае слова «начиная с некоторого момента…», содержащиеся в общем определении предела переменной расшифровываются следующим образом: для всех значений x достаточно близких к x 0 или, еще более точно, для всех точек x из некоторой достаточно малой окрестности точки x 0 (эту окрестность обычно называют d - окрестностью (дельта-окрестностью) точки x 0). Итак: Определение. Число a называется пределом функции f (x) При x ® x 0 (или в точке x 0), если для любого сколь угодно малого положительного числа e существует такое положительное число d, зависящее от e , что для всех точек x из d - окрестности точки x 0, исключая быть может саму точку x 0 (то
0 < x - x 0 < d),
f (x)- a < e. Геометрический смысл определения предела функции в точке x 0
представлен на рис. 22.
Рис. 22 Опять отметим e -окрестность точки a на оси OY (оси значений функций) и проведем e - полосу вокруг прямой y = a; отметим точки пересечения прямых y = a + e и y = a - e с графиком функции f (x), спроектируем эти точки на ось абсцисс и получим граничные точки d - окрестности точки x 0. Видим, что как только x попадает в d - окрестность точки x 0, значение функции y = f (x) попадает в e -окрестность точки a. Еще раз подчеркнем, что f (x) может и не быть определенной в точке x 0, но даже если она в этой точке определена, то значение f (x 0 ) в определении предела не участвует; важны лишь значения f (x) при значениях аргумента, близких к x 0. Поэтому не следует считать, что lim x ® x 0 f (x) обязан совпадать с f (x 0 ) (хотя, конечно, в большинстве случаев это так).
2.1.2.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 562; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.2.184 (0.06 с.) |

 y = tg x, y = ctg x, их графики приведены, соответственно, на рис. 11, 12, 13, 14.
y = tg x, y = ctg x, их графики приведены, соответственно, на рис. 11, 12, 13, 14.


 y = log 2 (cos 2 x + 1)
y = log 2 (cos 2 x + 1)
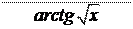


 y - a < e означает, что y находится в e - окрестности точки a, то есть в
y - a < e означает, что y находится в e - окрестности точки a, то есть в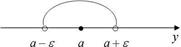
 2.1.2. Предел функции.
2.1.2. Предел функции. неравенство f (x)- a < e.
неравенство f (x)- a < e.
 график функции расположен внутри e - полосы (при этом f (x)- a < e).
график функции расположен внутри e - полосы (при этом f (x)- a < e).
 2.1.2. Предел функции.
2.1.2. Предел функции. есть для всех x, для которых выполняется неравенство
есть для всех x, для которых выполняется неравенство