
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расстояние от точки до плоскостиСодержание книги
Поиск на нашем сайте
Рис.1.7.17 Пусть дана точка M 0(x 0; y 0; z 0) и плоскость α: A 1 x + B 1 y + C 1 z + D 1 = 0.
Пример. Найти расстояние от точки M (3; 9; 1) до плоскости α: x – 2 y + 2 z – 3 = 0.
Решение: Применяем формулу (1.7.7), где A = 1, B = –2, C = 2, D = –3, Ответ: d = 5 1
1.7.2.
Рис.1.7.18 Пусть в системе координат Oxyz дана прямая, которая проходит через точку M 0(x 0; y 0; z 0) (см. рис.1.7.18). Обозначим через ` s = (m, n, p), ненулевой вектор, параллельный данной прямой. Вектор ` s называется направляющим вектором прямой.
Возьмем на прямой произвольную точку M (x, y, z) и рассмотрим вектор
Эти уравнения называются каноническими уравнениями прямой.
Рис.1.7.19 Пример. Написать уравнения прямой, проходящей через точку M (1; 2; –1) параллельно вектору ` s =(2,0,3) Решение: Вектор ` s является направляющим вектором искомой прямой. Применяя формулы (1.7.8), получим:
Это – канонические уравнения прямой. 2 0 3
Замечание: Обращение в нуль одного из знаменателей означает обращение в нуль соответствующего числителя, то есть y – 2 = 0; y = 2. Данная прямая лежит в плоскости y = 2, параллельной плоскости Oxz. Параметрические уравнения прямой Пусть прямая задана каноническими уравнениями
m Обозначим n p
тогда
y - y 0 = t; n z - z 0 = t.
Величина t называется
Выразим x, y и z через t:
Полученные уравнения называются параметрическими уравнениями прямой.
Решение: Канонические уравнения этой прямой получены в предыдущем примере:
2 0 3 Для нахождения параметрических уравнений прямой применим вывод формул (1.7.9.): x - 1 = t; 2 y - 2 = t; 0 z +1 = t Þ 3 x = 1 + 2 t; y = 2 + 0· t; z = –1 + 3 t.
Итак, ï y = 2
– параметрические уравнения прямой.
Ответ: ì x = 1+ 2 t
Пример. Составить параметрические уравнения прямой, проходящей через точку M (–1; 0; 1) параллельно вектору
AB, где A (2; 1; –1), B (–1; 3; 2).
Ответ: ï y = 0 + 2 t.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 150; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.249.105 (0.009 с.) |

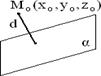
 Расстояние от точки M 0 до плоскости α (см. рис.1.7.17) находим по формуле:
Расстояние от точки M 0 до плоскости α (см. рис.1.7.17) находим по формуле:
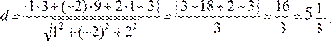
 3
3 Прямая в пространстве. Вывод уравнений прямой. Условия взаимного расположения прямых в пространстве.
Прямая в пространстве. Вывод уравнений прямой. Условия взаимного расположения прямых в пространстве.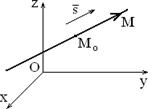




 соответствующие координаты пропорциональны:
соответствующие координаты пропорциональны:



 x -1 = y - 2 = z + 1.
x -1 = y - 2 = z + 1.

 x - x 0 = y - y 0 = z - z 0.
x - x 0 = y - y 0 = z - z 0. x - x 0 = t, m
x - x 0 = t, m p
p параметром и может принимать любые значения: –∞< t <∞.
параметром и может принимать любые значения: –∞< t <∞. Пример. Составить параметрические уравнения прямой, проходящей через точку M (1; 2; –1) параллельно вектору s =(2; 0; 3).
Пример. Составить параметрические уравнения прямой, проходящей через точку M (1; 2; –1) параллельно вектору s =(2; 0; 3).



 Решение: Вектор AB является направляющим вектором искомой прямой. Найдем его координаты: AB = (–3; 2; 3). По формулам (1.7.9) запишем параметрические уравнения прямой.
Решение: Вектор AB является направляющим вектором искомой прямой. Найдем его координаты: AB = (–3; 2; 3). По формулам (1.7.9) запишем параметрические уравнения прямой.


