
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. 2. Приращение функции. Непрерывность функции в точке и на интервале. Точки разрыва, их классификация.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 2.2.1. Приращение функции. Непрерывные функции. Два определения непрерывности функции в точке, их эквивалентность (равносильность). 2.2.2. Свойства непрерывных функций. 2.2.3. Непрерывность элементарных функций. 2.2.4. Точки разрыва функции и их классификация. 2.2.5.
Свойства функций, непрерывных на замкнутом интервале. 2.2.1. Приращение функции. Непрерывные функции. Два определения непрерывности функции в точке, их эквивалентность (равносильность). Определение 1. Функция y = f (x) называется непрерывной в точке x 0, если она определена в этой точке и некоторой еѐ окрестности, существует lim x ® x 0 lim x ® x 0 f (x), и этот предел равен значению функции в точке f (x) = f (x 0). x 0, то есть
Мы сейчас подробно расшифруем это определение “на языке будет почти таким же, как определение предела функции в точке e - d “, оно x 0, только вместо числа a, никак (в общем определении предела) не связанного со значением функции в предельной точке x 0, в нѐм будет фигурировать самое естественное число из всех, которые могут встретиться в этой ситуации, это число f (x 0 ). Функция y = f (x) называется непрерывной в точке x 0, если она определена в этой точке и некоторой еѐ окрестности и для любого (сколь угодно малого) положительного числа e существует такое положительное число d, зависящее от e (d = d (e)), что для всех значений x из d -окрестности
x 0, то есть для всех значений x, для которых выполняется неравенство
< d, будет выполняться неравенство f (x)- f (x 0 ) < e. Заметим, что в этом определении не нужна оговорка x ¹ x 0, которая была в определении предела, так как при x = x 0
Из этого определения следует, что в точке непрерывности можно менять местами символы функции и предела: lim f (x) = f æ lim x ö .
x ® x 0 è x ® x 0 ø В самом деле, если x 0 - точка непрерывности функции f (x), то
lim f (x) = f (x 0) = f ç
lim ö x ÷ .
Это используется при вычислении пределов, а именно: если нам надо найти предел функции f (x) в точке x 0, которая является точкой непрерывности этой функции, то надо в выражение этой функции подставить вместо x его предельное значение x 0.
Теперь перейдѐм ко второму определению непрерывности функции в точке. Нам понадобится ещѐ одно важное понятие - это понятие приращения переменной величины. Приращением переменной величины называется разность между двумя еѐ значениями. Приращение переменной величины x обозначается D x (дельта x). Пусть в начальный момент (начальный для нашего рассмотрения) переменная величина имела значение x 0, а затем в процессе своего изменения приняла какое-то значение x, разность между еѐ новым значением x и старым значением Величины. x 0 - это приращение D x = x - x 0 Этой переменной Теперь в качестве переменной величины возьмем функцию y = f (x). Приращение функции, согласно определению, это разность между двумя различными значениями функции, то есть между значениями функции в двух различных точках (например, x и x 0) (рис. 29).
D y = f (x)- f (x 0 ) = f (x 0 + D x)- f (x 0 ) = D f Рис. 29 – это приращение функции y = f (x) в Точке x 0, соответствующее приращению аргумента D x. Таким образом, чтобы получить приращение функции, надо придать приращение еѐ аргументу; приращение функции зависит от точки Приведем второе определение непрерывности функции в точке. x 0. Определение 2. Функция y = f (x) называется непрерывной в точке x 0, если она определена в этой точке и некоторой еѐ окрестности и бесконечно малому приращению аргумента D x соответствует бесконечно малое приращение функции D y в точке x 0, то есть lim D x ®0 D y = 0 (D y = f (x 0 + D x)- f (x 0)). Два определения непрерывности функции эквивалентны. Докажем, например, что из первого определения непрерывности функции в точке следует второе. Пусть lim x ® x 0 f (x) = f (x 0), тогда по теореме о разности между переменной величиной и еѐ пределом следует, что f (x) = f (x 0 )+ a, где a - бесконечно малая при x ® x 0, то есть при D x ® 0. Но a = f (x)- f (x 0 ) = D y, таким образом, D y является бесконечно малой при D x ® 0 или lim D x ®0 D y = 0. Аналогичными рассуждениями устанавливается, что из второго определения следует первое.
2.2.2. 1) Теорема о непрерывности результата арифметических действий над непрерывными функциями. Если функции f (x) и j (x) непрерывны в точке x 0, то их сумма f (x)+ j (x), разность f (x)- j (x), произведение f (x)× j (x), и, если j (x 0 ) ¹ 0, частное f ( x ) j (x) - также непрерывны в точке Доказательство. x 0. Докажем справедливость этой теоремы для случая произведения двух функций (все остальные утверждения доказываются аналогично). Рассмотрим функцию y (x) = f (x)× j (x). Чтобы проверить еѐ непрерывность в точке x 0, найдѐм lim x ® x 0 y (x): lim y (x) = lim f (x)×j(x) = lim f (x )× lim j(x ) = f (x 0 )×j(x 0 ) = y (x 0 ). x ® x 0 x ® x 0 x ® x 0 x ® x 0
(Сначала мы воспользовались теоремой о пределе произведения, а затем воспользовались непрерывностью функций f (x) и j (x) в точке x 0. Таким образом, lim x ® x 0 y (x) = y (x 0), то есть функция y (x) непрерывна в точке x 0).
|
|||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 756; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.007 с.) |




 точки
точки x - x 0
x - x 0


 f (x)- f (x 0 ) = f (x 0 )- f (x 0 ) = 0 < e.
f (x)- f (x 0 ) = f (x 0 )- f (x 0 ) = 0 < e.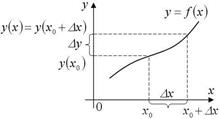
 Свойства непрерывных функций.
Свойства непрерывных функций.


