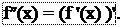Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический смысл производной. Уравнение касательной и нормали к кривой. Механический смысл производной.
Возьмем на непрерывной кривой L две точки M0 и М ₁. Прямую М0М ₁ проходящую через эти точки, называют секущей. Пусть точка М ₁ приближается по кривой к точке М0, тогда секущая М0М ₁ занимает разные положения. Определение. Касательной к кривой L в точке М0 называется предельное положение М0Т секущей М0М ₁, когда точка М ₁ неограниченно приближается по кривой к точке М0. Геометрический смысл производной. Значение производной f ¢(x 0) равно угловому коэффициенту касательной к графику функции f(x) в соответствующей точке М0(х0, f(х0)): k = f ¢(x 0 ). Уравнение касательной. Воспользуемся уравнением прямой, проходящей через точку М0(х0,y0) с заданным угловым коэффициентом k: y - y 0 = k (x - x 0).
Уравнение нормали Нормалью к кривой L в точке М0(х0,y0) называется прямая, проходящая через точку М0 и перпендикулярная касательной в этой точке. Так как нормаль перпендикулярна касательной, то еѐ угловой коэффициент k = - 1 = - 1 (если f ¢(x ) ¹ 0). норм. k к а с. f ¢(x 0 ) 0 Поэтому уравнение нормали имеет вид y - f (x 0 ) = - 1
f ¢(x 0) (x - x 0 ) , или
Пример. Составить уравнения касательной и нормали к кривой y =
y' = . Вычислим угловой коэффициент касательной: k кас. = f '(x 0) = = 1.
Составим уравнение касательной по формуле y – y0 = kкас. (x – x0): y – 3 = 1 (x – 4) или x – 6y + 14 = 0.
Найдѐм угловой коэффициент нормали: k норм. = - 1
= - 6. Запишем уравнение нормали по формуле y – y0 = kнорм.(x – x0): y – 3 = - 6(x - 4), или 6x + y – 27 = 0.
Механический смысл производной. Скорость v прямолинейного движения материальной точки в момент времени t есть производная от пути S по времени t: v = S ¢(t). Пример. Пусть S = 1 gt 2
(g – постоянное ускорение свободного
Правила дифференцирования. Производная суммы, произведения и частного функций Теорема. Если функции u(x) и v(x) имеют производные в точке х0, то в этой точке имеют производные их сумма, разность, произведение и частное (при условии, что частное имеет знаменатель v(x0)≠0), причем справедливы следующие формулы:
(u ± v) ¢ = u ¢ ± v ¢; (uv) ¢ = u ¢ v + uv ¢ ;. u ¢ u ¢ v - uv ¢
è ø v 2
Пример. Найти производную функции y = (5arctg x + 3 x)(log2 x - cos x). Решение. По формуле производной произведения получим:
= æ 5 + 3x ln3ö(log x - cosx) + (5arctgx + 3x) æ 1
+ sinx ö.
ç xln2 ÷ è ø è ø
Пример. Найти производную функции Решение. x 2 + x - 1
10 x По формуле производной частного получим: æ x 2 + x -1ö¢ (x 2 + x -1)¢×10 x - (x 2 + x -1) × (10 x)¢ y ¢ = ç è ÷ =
=
Производная сложной функции Теорема. Пусть функция u=u(x) имеет производную в точке х, а функция y=f(u) имеет производную в соответствующей точке u=u(x). Тогда сложная функция y=f(u(x)) имеет производную в точке х, которая находится по формуле: y¢x = f(u) × u¢(x). Пример. Найти производную функции y=lnarcsinx.
u 1 × 1 = 1 . arcsin x 2.3.6. Теорема. Пусть функция y = f (x) возрастает (или убывает) в некоторой окрестности точки x 0 и имеет непрерывную обратную функцию x = g (y). Если в точке x 0 функция y = f (x) имеет производную y ¢ x = f ¢(x 0) ¹ 0, то обратная функция имеет производную в соответствующей точке причем y 0 = f (x 0), x ¢ = g ¢(y) = 1 или x ¢ = 1.
Производная функции y = arctgx. Функция y = arctgx, определенная на бесконечной прямой -¥ < x < +¥, является обратной для функции x = tgy, определенной на интервале
- p < 2 y < p . Из формулы следует, что 2 y ¢ = (arctgx) ¢ = 1 = 1 = 1 = 1 = 1 = 1.
x x ¢ (tgy) ¢ æ 1 ö æ sin 2 y + cos 2 y ö tg 2 y + 1 x 2 + 1 y ç ÷ ç ÷
Итак,
(arctgx)¢ =
1.
è cos 2 y ø è cos 2 y ø
2.3.7. Теорема. Пусть зависимость между аргументом х и функцией у задана параметрическими уравнениями: ì x = j (t),
t Î(a, b), где t – вспомогательная переменная, называемая параметром. Пусть функции j (t) и y (t) имеют производные в некоторой точке t Î(a, b): y t ¢ = y ¢(t), x t ¢ = j ¢(t) ¹ 0. Кроме того, функция x = j (t) в окрестности точки t имеет обратную функцию t = g (x). Тогда определенная параметрическими уравнениями функция y=f(x)
 также имеет производную в точке x = j (t), причем также имеет производную в точке x = j (t), причем
Пример. Найти производную функции, заданной параметрически: ì x = t 3 + 5 t,.
Решение. Имеем: x ' t = 3 t 2 + 5, y ' t = 2 t - 1. Следовательно, производная равна: y ' x = y ' t
= 2 t - 1.
Пример. Найти производную функции, заданной параметрически: ì x = 3cos3 t,
Кривая, определяемая этими уравнениями, называется астроидой. Решение. Имеем: x't = 9cos 2t˙(- sin t) = - 9cos2 t sin t, y't = 9sin2 t ˙cos t. По формуле производная функции, заданной параметрическими уравнениями, равна:
9sin 2 t . cos t sin t
y x = x ' = - 9cos2 t . sin t = - cos t = - tgt.
Производные высших порядков Если функция f(x) в каждой точке некоторого промежутка имеет производную, то эта производная f '(x) является новой функцией на данном промежутке. Если функция f '(x) тоже имеет производную, то еѐ производная называется второй производной или производной второго порядка и обозначается y" или f"(x). Таким образом, по определению:
Производная от производной второго порядка, если она существует, называется третьей производной или производной третьего порядка и обозначается y"' (или f'"(x)):
Производной n -го порядка (или n -й производной) называется производная от производной (n – 1) порядка:
Начиная с производной четвѐртого порядка, производные обозначают римскими цифрами или числами в скобках (yIV или y(4) – производная четвѐртого порядка).
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 254; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.188.160 (0.05 с.) |
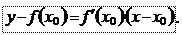 Так как для касательной y0=f(x0), k = t g a = f ¢(x 0 ), то уравнение касательной имеет вид
Так как для касательной y0=f(x0), k = t g a = f ¢(x 0 ), то уравнение касательной имеет вид

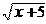 в точке с абсциссой x0 = 4.
в точке с абсциссой x0 = 4.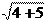 Решение. Найдѐм y0 = f(x0) = = 3.
Решение. Найдѐм y0 = f(x0) = = 3. Производная функции имеет вид:
Производная функции имеет вид: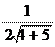
 6
6 k кас.
k кас. 2
2 падения), тогда скорость v(t) = S'(t) = gt.
падения), тогда скорость v(t) = S'(t) = gt.
 ç 1 + x2 ÷ 2
ç 1 + x2 ÷ 2 y = .
y = . 10 x ø
10 x ø (10 x)2 .
(10 x)2 . .
. 102 x
102 x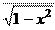
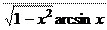 Решение. Положим: u=arcsinx, тогда y=ln u. Производная сложной функции равна:
Решение. Положим: u=arcsinx, тогда y=ln u. Производная сложной функции равна:
 y ' = (ln u)'× u ' = 1 × u ' =
y ' = (ln u)'× u ' = 1 × u ' = Дифференцирование обратной функции
Дифференцирование обратной функции







 1 + x 2
1 + x 2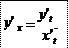
 x ' t
x ' t


 ЛЕКЦИЯ 9
ЛЕКЦИЯ 9