
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства функций, непрерывных на замкнутом интервале.Содержание книги
Поиск на нашем сайте
До сих пор, говоря о непрерывности, мы имели в виду непрерывность функции в точке. Пусть теперь функция f (x) задана на некотором интервале. Совершенно естественно было бы назвать функцию f (x) непрерывной на интервале, если она непрерывна в каждой точке этого интервала. Но такое определение не подходит для случая, когда интервал замкнут, то есть в него включены граничные точки (концы интервала). Дело в том, что давая определение непрерывности функции в точке, мы предполагали, что функция определена в целой окрестности этой точки, а в концах интервала это условие нарушается. Поэтому придѐтся пояснить, что мы будем понимать под непрерывностью функции f (x) в концах замкнутого интервала [ a, b ], то есть в точках a и b. Будем говорить, что функция f (x) непрерывна в левом конце интервала [ a, b ], то есть в точке a, если в этой точке существует правый предел f (a + 0) и он равен значению функции в левом конце, то есть f (a + 0) = f (a). Будем говорить, что функция f (x) непрерывна в правом конце интервала [ a, b ], то есть в точке b, если в точке b существует левый предел f (b - 0) и он равен значению функции в правом конце, то есть f (b - 0) = f (b). Получаем следующее определение. Определение. Функция f (x) называется непрерывной на замкнутом интервале [ a, b ], если она непрерывна в каждой внутренней точке этого интервала, имеет правый и левый пределы f (a + 0) и f (b - 0) (на левом и правом концах интервала соответственно) и f (a + 0) = f (a); f (b - 0) = f (b).
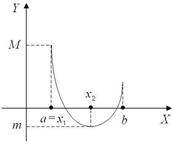
Теперь приведѐм (без доказательства) формулировки двух очень важных свойств функций, непрерывных на замкнутом интервале, которыми неоднократно будем пользоваться в курсе математического анализа. Свойство 1. Если функция f (x) непрерывна на замкнутом интервале [ a, b ], то она на этом интервале достигает своего наибольшего и наименьшего значений. Это означает, (см. рис. 32) что существует такая точка x 1 Î[ a, b ] (хотя бы одна), значение функции в которой f (x 1 ) = M является наибольшим среди всех значений, принимаемых функцией f (x) на этом интервале, то есть f (x 1 ) ³ f (x) для всех x из интервала [ a, b ]. Точно также существует хотя бы одна точка x 2 Î[ a, b ], значение функции в которой f (x 2) = m является наименьшим среди всех значений, принимаемых
функцией на этом интервале, то есть [ a, b ]. f (x 2 ) £ f (x) для любого x из интервала
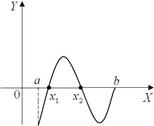
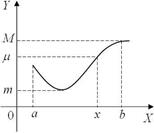
Рис. 32 На рис. 56 точка, в которой достигается наибольшее значение единственна, и это левый конец интервала [ a, b ] (x 1 = a); точка, в которой достигается наименьшее значение также единственна и она находится внутри интервала [ a, b ] (точка x 2). Следствие. Если функция непрерывна на замкнутом интервале, то она на этом интервале ограничена. Действительно, согласно свойству 1, функция на замкнутом интервале достигает своего наибольшего M и наименьшего значения m, поэтому для любого x из этого интервала выполняется неравенство m £ f (x) £ M. Свойство 2. Если функция непрерывна на замкнутом интервале, то она на этом интервале принимает любое значение, заключенное между еѐ наименьшим и наибольшим значениями на этом интервале. Это означает следующее: пусть m (m - греческая буква, читается “мю”) какое-либо число между m и M m £ m £ M, найдѐтся хотя бы одно значение x Î[ a, b ], для которого f (x) = m (рис. 33). Это свойство называют теоремой о промежуточном значении. Следствие. Если непрерывная на замкнутом интервале функция принимает на его концах значения с разными знаками, то внутри интервала обязательно найдѐтся хотя бы одна точка, в которой эта функция обращается в нуль (иными словами, внутри интервала найдѐтся хотя бы один корень уравнения f (x) = 0). На рис. 34 это точки x 1 и x 2.
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ. Производная функции, ее геометрический и механический смыслы. Правила дифференцирования Параметрическое задание функции. Циклоида, ее свойства и применение. 2.3.1. Определение производной. 2.3.2. Таблица производных. Вывод некоторых табличных производных. 2.3.3. Геометрический смысл производной. Уравнение касательной и нормали к кривой. Механический смысл производной. 2.3.4. Правила дифференцирования. 2.3.5. Производная сложной функции. 2.3.6. Дифференцирование обратной функции. 2.3.7. Производная функции, заданной параметрически. Циклоида, еѐ свойства и применение. 2.3.8. Производные высших порядков.
2.3.1. Рассмотрим функцию точки х.
y = f (x), определенную в некоторой окрестности Пусть аргумент х получил приращение ∆х, тогда функция получит приращение D y = f (x + D x)- f (x).
Обозначения производной: f ¢ (x), y ¢, y ¢ x , dy.
Если производная существует во всех точках некоторого промежутка (a,b), то еѐ можно рассматривать как новую функцию f ¢(x). Операция нахождения производной от функции f(x) называется дифференцированием этой функции. Теорема. Если функция y = f (x) имеет в некоторой точке x 0 производную, то она в этой точке непрерывна. Обратная теорема неверна: непрерывная функция может не иметь производной. В качестве примера рассмотрим функцию
x, если x ³ 0
Эта функция непрерывная. í- x, если x < 0 Докажем, что она не имеет производной в точке х=0. Действительно, в точке х=0 имеем
D x f (0 + D x) - f (0) =
0 + D x - 0 = D x
= ì 1, если D х > 0,.
D x ®0 D x производной в точке х=0.
2.3.2.
Приращение функции D у = a x +D x - a x = a x (a D x -1). Используя определение производной, найдем производную: y ' = lim D y =
lim a x (a D x - 1) =
lim a x × D x ln a
= a x ln a,
D x ®0 D x D x ®0 D x т.к. по таблице эквивалентных бесконечно малых a D x -1 при ∆ х →0. б) Пусть y = log a x, где а > 0, a ¹ 1. Тогда для любого x >0 приращение функции D y = log (x + D x) - log x = log x + D x = log
æ1 + D x ö.
a a a x a ç x ÷
log æ1 + D x ö
D y a ç x ÷ D x 1 y ¢ = lim
= lim D x ®0 è ø = D x lim =
,
так как по таблице эквивалентных бесконечно малых log æ1+ D x ö ~
D x. при
a ç x ÷ x ln a è ø ∆х →0.
Тогда Δy = sin(x + Δx) - sin x = 2sin Δx × cos(x + Δx).
По определению найдем производную 2sin Δx × cosæ x + Δx ö
2 × Δx × cosæ x + Δx ö
Δy 2 ç 2 ÷ 2 ç 2 ÷
Δx®0 Δx Δx®0 Δx Δx®0 Δx
ЛЕКЦИЯ 8
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 647; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.30.222 (0.011 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 ТЕМА 2. 3. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ТЕМА 2. 3. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Определение производной
Определение производной
 dx
dx

 D y =
D y = D x
D x
 D x D x
D x D x






 Таблица производных. Вывод некоторых табличных производных
Таблица производных. Вывод некоторых табличных производных
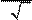

 Запишем формулы производных основных элементарных функций.
Запишем формулы производных основных элементарных функций.

 Вывод некоторых табличных производных.
Вывод некоторых табличных производных.


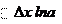 D x ®0 D x
D x ®0 D x
 D x ®0 D x
D x ®0 D x D x ®0 D x × x × ln a
D x ®0 D x × x × ln a x ln a
x ln a
 в) Пусть y= sin x.
в) Пусть y= sin x.
 2 2
2 2
 y' = lim = lim è ø = lim è ø = cosx,
y' = lim = lim è ø = lim è ø = cosx,

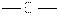 т.к. по таблице эквивалентных бесконечно малых sin D x D x при ∆ х →0.
т.к. по таблице эквивалентных бесконечно малых sin D x D x при ∆ х →0. 2 2
2 2


