
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь между бесконечно большими и бесконечно малыми переменными величинамиСодержание книги
Поиск на нашем сайте
Теорема. Величина, обратная бесконечно большой, является бесконечно малой; и наоборот, величина, обратная бесконечно малой, является бесконечно большой. Докажем эту теорему. Пусть y является бесконечно большой, это значит, что какое бы e > 0 мы не взяли (сколь угодно малое), начиная с некоторого момента в изменении y будет выполняться неравенство y > 1
(здесь в качестве M взято 1), из которого следует, что
1 < e. Рассмотрим переменную величину a = 1
(обратную к бесконечно большой y);
1, значит для любого e > 0, начиная с некоторого момента будет
является бесконечно малой. < e, что, в свою очередь, означает, что a = 1
Точно также можно доказать второе утверждение теоремы. Пусть a - бесконечно малая, тогда какое бы мы не взяли M > 0 (сколь угодно большое), начиная с некоторого момента в изменении a будет выполняться неравенство a < 1
(здесь 1 взято в качестве e ), откуда следует, что
y = 1
(обратную к бесконечно
= 1, значит для любого M > 0, начиная с некоторого
y > M, что означает, что y - бесконечно Например, y = x 2 является бесконечно малой при x ® 0, а y = 1
является бесконечно большой при x ® 0. Величина y = x 2 является бесконечно большой при x ® ¥ , а y = 1
является бесконечно малой при x ® ¥ .
ЛЕКЦИЯ 6 Два признака существования пределов. Иногда нас не интересует само значение предела переменной величины, но нам важно в принципе знать существует предел этой переменной или нет. Удобно иметь простые признаки, которые позволяют по некоторым элементам поведения переменной величины устанавливать имеет ли она предел (не вычисляя самого предела). Наиболее употребительны следующие два признака: Теорема о промежуточной переменной. Если значения переменной величины заключены между значениями двух переменных величин, стремящихся к одному и тому же пределу, то данная переменная величина стремится к тому же самому пределу. Итак, заданы три переменные величины x, y, z, причем значения z лежат между значениями x и y: пределу a (lim x = lim y = a рис. 25, 26. x £ z £ y; переменные x и y стремятся к одному ). Две из возможных ситуаций представлены на
Ясно, что поскольку x ® a, y ® a, и z лежит между x и y,то z ® a. Мы не будем приводить строгое доказательство этого признака, хотя это нетрудно сделать, используя определение предела.
|
||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 302; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.248.88 (0.009 с.) |




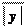 e
e e
e y
y

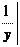

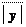 a = =
a = =
 выполняться неравенство a
выполняться неравенство a M
M M
M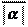 1 > M. Рассмотрим переменную величину
1 > M. Рассмотрим переменную величину a
a

 малой a). y =
малой a). y =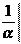

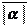
 момента, выполняться неравенство большая.
момента, выполняться неравенство большая. x 2
x 2





