
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема. Второй достаточный признак экстремума.
Рассмотрим функцию y = f (x), определенную в некоторой окрестности точки x 0. Пусть функция f (x) имеет в точке x 0 вторую производную. Если f ¢(x 0) = 0, f ¢ (x 0 ) < 0, то x 0 - точка максимума функции. Если f ¢(x 0) = 0, f ¢ (x 0) > 0, то x 0 - точка минимума функции f (x).
Заметим, что f ¢ (x 0) = 0 может быть как в точках, где экстремума нет, так и в точках экстремума. Например, для функции y = x 3 в точке x = 0 экстремума нет, хотя в этой точке y ¢ = 3 x 2 = 0, y ¢ = 6 x = 0; а для функции y = x 4 точка x = 0 - точка минимума, но также y ¢ = 4 x 3 = 0, y ¢ = 12 x 2 = 0. В этом случае исследование нужно вести с помощью первого достаточного признака экстремума.
Исследуем вторым способом на экстремум функцию y = x 3 - 3 x + 2. Первая производная y'=3x2 – 3=3(x2 – 1)=3(x – 1)(x + 1). Находим вторую производную y ¢ = 6 x. Критическими точками являются x 1 = -1, x 2 = 1.Так как f ¢(-1) = 0, f ¢ (-1) = -6 < 0, то x 1 = -1 - точка максимума
f ¢ ( 1 ) = 0, f ¢ ( 1 ) = 6 > 0, то x 2 = 1 - точка минимума функции. ЛЕКЦИЯ 11 - 16 ТЕМА 2. 7. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ. Выпуклость, точки перегиба кривой. Асимптоты. Общая схема исследования функции одной переменной. 2.7.1. Выпуклость графика функции. Достаточный признак выпуклости. 2.7.2. Точки перегиба кривой. Необходимый признак точки перегиба. Достаточный признак точки перегиба. 2.7.3. Асимптоты графика функции. 2.7.4. Общая схема исследования функции одной переменной. Построение графика.
2.7.1. Определение. График дифференцируемой функции y = f(x) называется выпуклым вверх на интервале (а, b), если все точки графика лежат ниже любой касательной к графику функции на этом на интервале. Определение. График дифференцируемой функции y = f(x) называется выпуклым вниз на интервале (а, b), если все точки графика лежат выше любой касательной к графику функции на этом интервале.
Теорема. Достаточный признак выпуклости. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый вверх. Если во всех точках интервала (a, b) вторая производная функции f(x) положительна, т.е. f ''(x)>0, то график функции на этом интервале выпуклый вниз.
Пример. Доказать, что график функции y = x Решение. Находим первую и вторую производные: y' = (xarctgx)' = (x) ' arñtgx + x(arñtgx)' = 1 × arctg x + x;
æ x ¢ 1 x' (1 + x 2) - x (1 + x 2) ' 1 1 + x 2 - 2 x 2
è 1 + x 2 ÷ 1 + x 2 (1 + x 2)2 1 + x 2 (1 + x 2)2
(1 + x 2)2 = 2
> 0. Следовательно, по достаточному признаку график функции выпуклый вниз при x Î(-¥,+¥).
2.7.2.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 153; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.143.31 (0.01 с.) |
 функции. Так как
функции. Так как Выпуклость графика функции. Достаточный признак выпуклости.
Выпуклость графика функции. Достаточный признак выпуклости.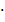 arctgx везде выпуклый вниз.
arctgx везде выпуклый вниз. 1 + x 2
1 + x 2

 = 1 + x 2 + 1 - x 2
= 1 + x 2 + 1 - x 2 (1 + x 2)2
(1 + x 2)2


