Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достаточный признак точки перегиба.Содержание книги
Поиск на нашем сайте
Определение. Точка, отделяющая выпуклую вверх часть графика непрерывной функции от выпуклой вниз, называется точкой перегиба графика функции. Если в точке перегиба существует касательная к графику, то график функции с одной стороны от точки перегиба лежит над касательной, а с другой стороны – под касательной.
Теорема. Необходимый признак точки перегиба. Если х0 – абсцисса точки перегиба графика функции y = f(x), то вторая производная f "(x0) равна нулю или не существует.
Замечание 1. Таким образом, абсциссы точек перегиба графика функции следует искать среди точек, в которых вторая производная равна нулю или не существует. Замечание 2. Равенство f "(x0) = 0 является необходимым, но не достаточным признаком точки перегиба функции, имеющей вторую производную. Рассмотрим, например, функцию y = x4. Найдѐм производные: y' = 4x3, y " = 12x2 = 0 при х = 0. Однако точка О (0; 0) не является точкой перегиба.
Теорема. Достаточный признак точки перегиба. Пусть функция y=f(x) непрерывна в точке х0, имеет вторую производную в некоторой окрестности точки х0, за исключением, быть может, самой точки х0. Если при переходе через точку х0 вторая производная f ''(х) меняет знак, то точка графика функции М (х0, f(x0)) – точка перегиба.
Доказательство. Так как вторая производная f ¢ (x) слева и справа от точки x 0 имеет разные знаки, то направление выпуклости графика функции слева и справа от точки x 0 различны. Но тогда, по определению, точка графика функции M (x 0, f (x 0)) - точка перегиба.
Пример. Найти точки перегиба и интервалы выпуклости вверх и вниз графика функции y=x3-3x2-12x+3. Решение. Находим производные: y=3x2-6x-12, y"=6x-6. Вторая производная обращается в нуль при x0=1. Так как f "(x)<0 при x<1, то график функции выпуклый вверх на интервале (-∞, 1). Так как f "(х)> 0 при х>1, график функции выпуклый вниз на интервале (1,+∞). Следовательно, х0=1 – абсцисса точки перегиба.
Асимптоты графика функции Определение. Прямая называется асимптотой кривой, если расстояние от точки, лежащей на кривой, до прямой стремится к нулю при неограниченном удалении этой точки по кривой от начала координат. Асимптоты бывают вертикальные и наклонные.
Вертикальные асимптоты Прямая x=a является вертикальной асимптотой графика функции y=f(x), если lim f (x) =¥ или x ® a -0 lim f (x) = ¥. x ® a +0 Для отыскания вертикальных асимптот нужно найти те значения аргумента х, при приближении к которым функция f(x) неограниченно возрастает по модулю. Эти значения нужно искать среди точек разрыва второго рода и на границе области определения функции.
Пример. График функции Действительно, y = 1
имеет вертикальную асимптоту x=2. 1 1 lim = +¥ lim = -¥.
x ®2+0 x - 2 , x ®2-0 x - 2 Точка х=2 – точка разрыва 2 рода функции.
Пример. График функции y=ln x имеет вертикальную асимптоту х=0. Действительно, lim ln x = -¥. Область определения функции – интервал x ®0+0 (0,+∞). Точка х=0 – граница области определения.
Наклонные асимптоты Теорема. Для того чтобы график функции y=f(x) имел при x →+∞ (x →-∞) наклонную асимптоту y=kx+b, необходимо и достаточно, чтобы существовали пределы
lim (f (x) - kx) = b. x ®+¥ (x ®-¥ ) Лемма. График функции x y = f (x) x ®+¥ (x ®-¥ ) имеет наклонную асимптоту
y = kx + b при x ® +¥ тогда и только тогда, когда функция представима в виде f (x) = kx + b + a (x),, где lim a (x) = 0. x ®+¥ Доказательство леммы. Пусть M (x, y) - точка, лежащая на графике функции, а N (x, y) - точка,
от точки M до асимптоты. По определению, прямая наклонной асимптотой, если y = kx + b является lim MP = 0. x ®+¥ Пусть j - угол наклона асимптоты к оси Ox, тогда из D MNP найдем: NM = MP
cos j . С другой стороны,
Равенство lim MP = 0 выполняется тогда и только тогда, когда
lim NM = x ®+¥ lim x ®+¥ f (x) - (kx + b) = 0. Из последнего равенства по определению бесконечно малой функции следует, что f (x) - (kx + b) = a (x), lim a (x) = 0. x ®+¥ Таким образом, f (x) = kx + b + a (x). Доказательство теоремы. Необходимость. Пусть график функции y = f (x) имеет при x ® +¥ асимптоту y = kx + b. Тогда по лемме выполняется равенство f (x) = kx + b + a (x), lim a (x) = 0. Найдем пределы:
lim f (x) = lim kx + b + a (x) = lim æ k + b + a (x) ö = k;
x ®+¥ x x ®+¥ è x x ø
lim (f (x) - kx) = x ®+¥ lim (kx + b + a (x) - kx) = x ®+¥ lim (b + a (x)) = b. x ®+¥
Достаточность. Из равенства lim (f (x) - kx) = b x ®+¥ по теореме о связи предела и бесконечно малой функции следует, что f (x) - kx = b + a (x), lim a (x) = 0.То есть f (x) = kx + b + a (x) , x ®+¥ следовательно, прямая y = kx + b по лемме является наклонной асимптотой графика функции y = F (x). Аналогично доказывается теорема для случая x ® -¥. Замечание. Горизонтальную асимптоту y=b получим в случае, когда k = lim x ®+¥ f (x) = 0 , b =
lim x ®+¥ f (x). (x ®-¥ ) (x ®-¥ ) Пример. Найти асимптоты графика функции y = 2 x - 1.
Решение. Функция определена, если знаменатель x -1 ¹ 0, x ¹ 1. Таким образом, область определения - объединение интервалов Точка х= 1 –точка разрыва. (-¥,1) È (1,+¥). Так как
lim x ®1+0 2 x -1 = +¥,
lim x ®1-0 2 х -1 = -¥ ,
прямая x= 1 является вертикальной асимптотой. Далее имеем:
 2 x - 1 2 - 1 2 x - 1 2 - 1
k = f (x) = 2 x -1 = 2 x -1 =
x 2 x 2 =
x x 2 = 0, lim lim lim 2 lim 2 lim x ®¥ x x ®¥ x(x -1 ) x ®¥ x - x x ®¥ x - x x ®¥ 1 - 1
2
1
x 2 x 2 x x ®¥ x x ®¥ x 2 2 x - 1
2 - 1 ,
b = lim (f (x) - kx) = lim 2 x -1 = lim x x =
lim x = 2.
x ®¥ x -1 x ®¥ x - 1 x ®¥ 1 - 1
2.7.4. Общая схема исследования функции одной переменной. Построение графика. Исследование функции целесообразно вести в определенной последовательности. 1. Найти область определения функции, точки разрыва. 2. Найти вертикальные асимптоты. 3. Найти точки пересечения графика с осями координат, интервалы знакопостоянства функции. 4. Исследовать функцию на четность или нечетность, найти симметрию графика. 5. Найти наклонные асимптоты графика. 6. Найти точки экстремума, интервалы монотонности функции. 7. Найти интервалы выпуклости и точки перегиба графика функции.
Пример. Исследовать функцию Решение. (x - 2)2
и построить еѐ график. 1. Функция определена, если знаменатель x -1 ¹ 0, x ¹1. Таким образом, область определения – объединение интервалов (- ¥,1)È (1,+¥). Точка x = 1 - точка разрыва функции.
2. Так как
Lim x ®1+0 ( x - 2)2
= +¥, lim x ®1-0 ( x - 2)2
= -¥, прямая х= 1 – вертикальная асимптота графика функции.
3. Если x = 0, то y = 0 - 1
= -4. График пересекает ось ОY в точке A (0, -4) . Если y = x -1 = 0, то x = 2. График пересекает ось OX в
точке B (2, 0) . Функция ( x - 2)2
x > 1, следовательно, график функции расположен выше оси OX при ( x - 2)2 x > 1. Функция
< 0 при x < 1, следовательно, график функции расположен ниже оси OX при x < 1. 4. f (- x) = (- x - 2)2
f ( x), f (- x) ¹ - f (x) , поэтому функция общего вида (не является ни чѐтной, ни нечѐтной). 5. Ищем наклонную асимптоту y = kx + b. Имеем:
x 2 - 4 x + 4
- 4 + 4 k = lim f (x) (x - 2 ) 2
= lim x 2 - 4 x + 4
2 = lim x 2 x 2
1
x x 2 1 = 1, x ®¥ x x ®¥ x(x -1 ) x ®¥ x - x x ®¥ x - x x ®¥ 1- x 2 x 2 x æ (x - 2 ) 2
-1× x ö = lim (x - 2 ) 2 - x(x -1 ) =
x ®¥
2 2 x ®¥ è x -1 ø x ®¥ - 3 x + 4 x -1
- 4 x + 4 - x + x = lim -3 x + 4 = lim
x x = lim
x = -3.
x -1 x ®¥ x -1 x ®¥ x - 1 x ®¥ 1- 1 Прямая x x x y = x - 3- наклонная асимптота графика функции. 6. Находим производную ¢ 2 ¢ 2 ¢ 2 æ (x - 2 ) 2 ö ((x - 2) ) (x -1) - (x - 2) (x -1) 2 ( x - 2)( x - 1) - ( x - 2) y ¢ = ç x -1 ÷ = (x -1)2 = =
= ( x - 2) (2 ( x - 1) - ( x - 2)) = ( x - 2)(2 x - 2 - x + 2) = ( x - 2) x. (x -1)2 (x -1)2 (x -1)2
Находим критические точки. Производная y ¢ = 0 при x 1 = 2, x 2 = 0. Производная не существует при x 3 =1. Критические точки разбивают ось Ox на четыре интервала (- ¥,0),(0,1),(1,2),(2,+¥). Отметим на рис. 2.7.1 знаки производной на каждом интервале.
Следовательно,
x 1 = 2 Рис.2.7.1. - точка минимума,
f (2) = 0. Критическая точка x 2 =0 – точка максимума, f (0) = -4. Критическая точка x 3 =1 - точка разрыва. Функция возрастает на интервалах (- ¥,0) интервалах (0,1) и (1,2). и (2,+¥). Функция убывает на
7. Находим вторую производную æ ( x - 2) x ö¢ æ x 2 - 2 x ö¢
(x 2 - )¢( - 1)2 - (x 2 - 2 x)((x - 1)2)¢ y ¢ = ç ÷ = ç ÷ = 2 x x =
(x - 1)4 è ø è ø
= (2 x - 2)(x - 1)2 - (x 2 - 2 x)2(x - 1) = (x - 1)[(2 x - 2)(x - 1) - (x 2 - 2 x)2] = (x - 1)4
(x - 1)3
2.
(x - 1)4 Вторая производная не существует при x = 1. Эта точка разбивает ось ОХ на два интервала (- ¥,1) и (1,+¥). Отметим на рисунке 2 знаки второй производной на каждом интервале.
Рис. 2.7.2.. Следовательно, график функции выпуклый вверх на интервале (- ¥,1), выпуклый вниз на интервале (1,+¥). Точка поэтому точек перегиба нет. x = 1 - точка разрыва функции,
Рис. 3.7.3.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 181; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.135.201 (0.012 с.) |


 Найдем ординату y0=13-3
Найдем ординату y0=13-3 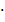 12-12 1+3=-11. Точка M(1,-11) – точка перегиба графика функции.
12-12 1+3=-11. Точка M(1,-11) – точка перегиба графика функции. x - 2
x - 2

 lim f (x) = k;
lim f (x) = k; лежащая на асимптоте. Пусть точка P - основание перпендикуляра, опущенного из точки M на асимптоту. Длина отрезка MP равна расстоянию
лежащая на асимптоте. Пусть точка P - основание перпендикуляра, опущенного из точки M на асимптоту. Длина отрезка MP равна расстоянию
 NM = TM - TN
NM = TM - TN

 = y - y =
= y - y =

 x ®+¥
x ®+¥


 x ®+¥ x
x ®+¥ x x
x x - 1
x - 1 x -1
x -1 x -1
x -1





 lim = 0,
lim = 0, lim = 0,
lim = 0,
 x ®¥
x ®¥

 x x x
x x x Следовательно, прямая y=kx+b, то есть y= 2 – горизонтальная асимптота.
Следовательно, прямая y=kx+b, то есть y= 2 – горизонтальная асимптота. y = x - 1
y = x - 1 x -1
x -1 x -1
x -1 (0 - 2)2
(0 - 2)2 ( x - 2)2
( x - 2)2 y = x -1 > 0, при
y = x -1 > 0, при y = x -1
y = x -1 - x -1 ¹
- x -1 ¹



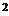

 x 2 = lim
x 2 = lim b = lim(f (x) - kx) = lim ç
b = lim(f (x) - kx) = lim ç
 = lim x
= lim x



 x ®¥
x ®¥ (x -1)2
(x -1)2 è ø
è ø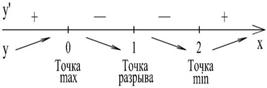
 ç (x - 1)2 ÷ ç (x - 1)2 ÷
ç (x - 1)2 ÷ ç (x - 1)2 ÷

 = 2 x 2 - 2 x - 2 x + 2 - 2 x 2 + 4 x =
= 2 x 2 - 2 x - 2 x + 2 - 2 x 2 + 4 x = (x - 1)3
(x - 1)3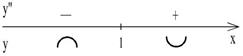

 График исследуемой функции изображѐн на рис.3.7.3.
График исследуемой функции изображѐн на рис.3.7.3.