Точки разрыва функции и их классификация.

Напомним, что значит, что функция y = f (x)

непрерывна в точке x 0:

278.  функция f (x) определена в точке x 0 и некоторой еѐ окрестности;

1. существует предел этой функции при

x ® x 0

lim

x ® x 0

f (x), что в свою

очередь означает, что в этой точке функция f (x) имеет правый предел

f (x 0  + 0), имеет  левый  предел f (x 0  - 0), и  эти  пределы  равны  между

собой, то есть   f (x 0  + 0) =   f (x 0  - 0);

2. предел функции f (x) в точке x 0 равен значению функции в точке

x 0:

lim

x ® x 0

f (x) = f (x 0)

Определение. Точка

x 0 называется точкой разрыва функции

y = f (x),

если в этой точке нарушены условия непрерывности.

Это означает, что не выполняется хотя бы одно из трѐх перечисленных

выше условий непрерывности, то есть: либо функция   f (x) не определена в

точке

x 0, либо она не имеет предела в точке x 0

(то есть либо у неѐ нет

конечных правого или левого пределов в этой точке, либо они есть, но они не

равны между собой), либо f (x) имеет предел в точке   x 0, но он не равен

значению функции в этой точке

 

lim

 

f (x) ¹

 

f (x 0).

 

Пример 1.

 

f (x) =

 

1

 

x + 2

 

, x 0

x ® x 0

 

= -2

 

- точка разрыва, так как функция в этой

точке не определена.

Пример 2.

f (x) = ì 1

при

x ³ 0

î

í-1

при

x < 0

График этой функции изображен на рис. 30.

x 0 = 0 точка разрыва, так как, хотя f (x) определена в точке

x 0 = 0

(f (0) = 1),

но в этой точке не существует

lim f (x) (правый предел в нуле f (0 + 0) = 1; левый

x ®0

предел в нуле

f (0 - 0) = -1;

f (0 - 0) ¹

f (0 + 0)).

 

 

Пример 3.

ì

í

f (x) = ï

ïî

 

sin x x

2

 

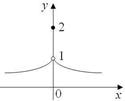
при при

x ¹ 0.

x = 0

График этой функции изображен на рис. 31.

x 0 = 0

точка разрыва, так как, хотя функция

f (x)

и определена в точке

x 0 = 0 (f (0) = 2) и существует еѐ предел в этой точке

lim

x ®0

sin x = 1

x

(это первый

замечательный предел), но

Пример 4.

f (0) = 2 ¹

lim

x ®0

f (x) = 1.

 

                                                      

 

 

Рис. 30

Рис. 31

 

Общепринятой является следующая классификация точек разрыва.

 

Если в точке

x 0 существуют (конечные) равные между собой левый и

правый пределы, но они не равны значению функции в точке

x 0, то точка x 0

называется точкой устранимого разрыва функции. Этот случай характерен

тем, что функция f (x) либо “плохо” определена в точке x 0 (рис. 31),  либо

вообще не определена в точке

x 0. Но достаточно исправить или доопределить

функцию в одной точке

x 0, чтобы она стала непрерывной (отсюда и название

- точка устранимого разрыва).

Если в точке x 0 существуют (конечные), но не равные между собой левый

и правый пределы

(f (x 0  - 0) ¹

f (x 0 +0)),  то  такая  точка  называется   точкой

разрыва первого рода (рис. 30).

Все остальные точки разрыва называются точками разрыва второго рода.

Вернѐмся к рассмотренным нами примерам 1, 2, 3.

В примере 1 точка разрыва точке.

x 0 = -2, найдѐм левый и правый пределы в этой

f (- 2 + 0) =

lim      1 = +¥

(рассуждаем здесь следующим образом: при

x ®-2+0 x + 2

x ® -2 + 0

(то есть x ® -2, но

x > -2) (x + 2)

является положительной

бесконечно малой, значит обратная к ней функция

1

 

x + 2

является

положительной бесконечно большой); f (- 2 - 0) =

lim      1 = -¥ (здесь при

x ® -2 - 0 (то есть x ® -2, но x < -2) (x + 2)

x ®-2-0 x + 2

является отрицательной

бесконечно малой, значит обратная к ней функция отрицательной бесконечно большой).

1

 

x + 2

является

Таким образом, в точке

x 0 = -2

не существует конечных односторонних

пределов, значит, согласно приведѐнной классификации точек разрыва,

x 0 = -2

является точкой разрыва второго рода.

В примере 2 точка x 0 = 0 является точкой разрыва первого рода, так как

f (0 - 0) = -1, f (0 + 0) = 1; оба односторонних предела конечны, но не равны между собой.

В примере 3 x 0 = 0 - точка устранимого разрыва, так как f (0 - 0) = f (0 + 0) = 1

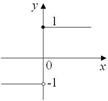
, но f (0) = 2 ¹ 1.