
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение плоскости по точке и нормальному вектору.Содержание книги
Поиск на нашем сайте
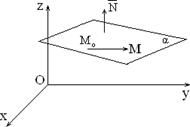
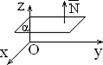
Рис.1.7.2 В системе координат Oxyz рассмотрим плоскость α (рис.1.7.2). Ее положение определяется заданием вектора `N, перпендикулярного этой плоскости, и фиксированной точки M 0(x 0; y 0; z 0) лежащей в этой плоскости. Вектор `N = (A; B; C), перпендикулярный плоскости α, называется нормальным вектором (вектором-нормалью)
лежащий в плоскости α, будет перпендикулярен вектору-нормали `N.
Уравнение
N × M 0 M = 0, получим
Называется уравнением плоскости по точке и нормальному вектору. Если в уравнении (1.6.1) раскроем скобки и перегруппируем слагаемые, то получим уравнение Ax + By + Cz + (– A x 0 – By 0 – Cz 0) = 0 или Ax + By + Cz + D = 0, где D = – A x 0 – By 0 – Cz 0. Общее уравнение плоскости Уравнение
называется общим уравнением плоскости, здесь ` N = (A; B; C) – нормальный вектор.
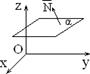
1) Пусть D = 0. Уравнение имеет вид: Ax + By + Cz = 0. Такая плоскость проходит через начало координат.
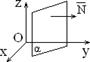
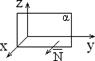
2) перпендикулярен оси Oz Þ плоскость параллельна оси Oz (рис.1.7.3)
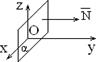
плоскость параллельна оси Oy (рис. 1.7.4) 4) A = 0: By + Cz + D = 0 Þ ` N = (0; B; C) ^ Ox, плоскость параллельна оси Ox (рис. 5)
ось Oz (рис. 1.7.6) ^ Oz, плоскость проходит через
6) B = D = 0: Ax + Cz = 0 Þ ` N = (A; 0; C) ^ Oy, плоскость проходит через ось Oy (рис. 1.7.7) 7) A = D = 0: By + Cz = 0 Þ ` N = (0; B; C) ^ Ox, плоскость проходит через ось Ox (рис. 1.7.8) 8) A = B = 0: Cz + D = 0 Þ ` N = (0; 0; C) || Oz, плоскость параллельна плоскости Oxy (рис. 1.7.9)
8) B = C = 0: Ax + D = 0 Þ `N = (A; 0; 0) || Ox, плоскость параллельна плоскости Oyz (рис. 1.7.10) 8) A = C = 0: By + D = 0 Þ `N = (0; B; 0) || Oy, плоскость параллельна плоскости Oxz (рис. 1.7.11)
Пример. Составить уравнение плоскости, проходящей через точку M 0(1; 2; –1) перпендикулярно вектору `N = (2; –1; 3). Найти точки пересечения этой плоскости с осями координат. Решение. По формуле (1.7.1) имеем 2(x – 1) –1·(y – 2) + 3(z + 1) =0, 2 x – y + 3 z + 3 = 0. Для того, чтобы найти пересечение этой плоскости с осью Ox, подставим в полученное уравнение y = 0, z = 0. Получим 2 x + 3 = 0; x = –1,5. Точка пересечения искомой плоскости с осью Ox имеет координаты: M 1(–1,5; 0; 0). Найдем пересечение плоскости с осью Oy. Для этого возьмем x = 0, z = 0. Имеем – y + 3 = 0 Þ y = 3. Итак, M 2(0; 3; 0). Для нахождения точки пересечения с осью Oz возьмем x = 0, y = 0. Тогда 3 z + 3 = 0 Þ z = – 1. Итак, M 3(0; 0; –1).
Ответ: 2 x – y + 3 z + 3 = 0, M 1(–1,5; 0; 0), M 2(0; 3; 0), M 3(0; 0; –1).
Пример. Исследовать плоскости, заданные уравнениями: a) 3 x – y + 2 z = 0, б) 2 x + z – 1 = 0, в) – y + 5 = 0, г) x = 0. Решение. а) Данная плоскость проходит через начало координат (D = 0) и имеет нормальный вектор `N = (3; –1; 2). б) В уравнении 2 x + z – 1 = 0 коэффициент B = 0. Следовательно, `N = (2; 0; 1). Плоскость параллельна оси Oy. в) В уравнении – y + 5 = 0 коэффициенты A = 0, C = 0. Значит, `N = (0; – 1; 0). Плоскость параллельна плоскости Oxy.
г) Уравнение x = 0 задает плоскость Oyz, так как при B = 0, C = 0 плоскость параллельна плоскости Oyz, а из условия D = 0 следует, что плоскость проходит через начало координат.
Пример. Составить уравнение плоскости, проходящей через точку A (2; 3;
Решение. Найдем вектор
BC.
–3(x – 2) + 2(y – 3) + 1·(z – 1) = 0; –3 x + 2 y + z + 6 – 6 – 1 = 0; –3 x + 2 y + z – 1 = 0; 3 x – 2 y – z + 1 = 0.
Ответ: 3 x – 2 y – z + 1 = 0.
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.125.86 (0.006 с.) |


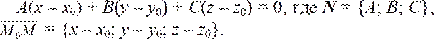 Используя условие ортогональности векторов уравнение:
Используя условие ортогональности векторов уравнение:

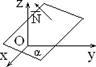 Рассмотрим частные случаи этого уравнения.
Рассмотрим частные случаи этого уравнения.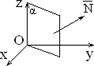
 С = 0: Ax + By + D = 0 Нормальный вектор этой плоскости ` N = (A, B, 0)
С = 0: Ax + By + D = 0 Нормальный вектор этой плоскости ` N = (A, B, 0) 3) B = 0: Ax + Cz + D = 0 Þ ` N = (A, 0, C) ^ Oy,
3) B = 0: Ax + Cz + D = 0 Þ ` N = (A, 0, C) ^ Oy, 5) C = D = 0: Ax + By = 0 Þ ` N = (A, B, 0)
5) C = D = 0: Ax + By = 0 Þ ` N = (A, B, 0)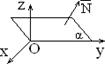
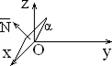


 1) и перпендикулярной вектору BC, где B (1; 0; –1), C (–2; 2; 0).
1) и перпендикулярной вектору BC, где B (1; 0; –1), C (–2; 2; 0). Вектор BC является нормальным вектором искомой плоскости, проходящей через точку A (2; 3; 1) По формуле (2.2.1) имеем:
Вектор BC является нормальным вектором искомой плоскости, проходящей через точку A (2; 3; 1) По формуле (2.2.1) имеем:


