
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операции над векторами и их свойства. Разложение вектора по базису. Векторы в прямоугольной системе координат.Содержание книги
Поиск на нашем сайте
1.4.1. Векторы: некоторые определения. 1.4.2. Линейные операции над векторами. Орт вектора. 1.4.3. Необходимое и достаточное условие коллинеарности двух векторов. 1.4.4. Разложение вектора на плоскости по двум неколлинеарным векторам 1.4.5. Разложение вектора в пространстве по трем некомпланарным векторам
1.4.1. Векторы: некоторые определения. Из курса физики известно, что некоторые физические величины, например, температура, масса, плотность являются скалярными, другие величины, например, сила, скорость, ускорение, являются векторными. Каждая скалярная величина характеризуется одним числом, которое выражает отношение этой величины к соответствующей единице измерения. Для характеристики векторной величины одного числа недостаточно, так как, кроме размерности, векторные величины обладают еще и направлением. Для рассмотрения физических векторных величин применяются геометрические векторы.
Рис.1.4.1
Определение. Геометрическим вектором (или просто вектором), называется направленный отрезок. Рис. 1.4.2
Начало вектора называется точкой приложения вектора.
Длина вектора называется модулем вектора и обозначается: (очевидно, что | ā | ³ 0 для любого вектора ā). , | ā |
Определение. Коллинеарными называются векторы, лежащие на одной прямой или параллельных прямых. Обозначение: ā ||` b. Определение. Сонаправленными называются коллинеарные векторы, имеющие одинаковое направление. Обозначение: ā ↑↑` b. Определение. Противоположно направленными называются коллинеарные векторы, имеющие противоположные направления. Обозначение: ā ↑↓` b.
Рис. 1.4.3 Определение. Равными называются векторы, если они сонаправлены и имеют одинаковые длины.
    Пример. Рассмотрим параллелограмм ABCD и векторы AB, AD, DC,CB, идущие по его сторонам (рис. 1.4.4). Пример. Рассмотрим параллелограмм ABCD и векторы AB, AD, DC,CB, идущие по его сторонам (рис. 1.4.4).Рис. 1.4.4
Рис. 1.4.5 Из определения равенства двух векторов следует, что для каждого вектора его точка приложения может быть выбрана произвольно. Не различаются два вектора, получающиеся один из другого параллельным переносом (рис. 1.4.6). В соответствии с этим определением векторы, изучаемые в курсе векторной алгебры, называются свободными. Определение. Компланарными называются векторы, лежащие в одной плоскости или параллельных плоскостях. Отметим, что два вектора всегда компланарны, а три вектора могут быть компланарными, а могут и не быть компланарными.
1.4.2. Линейными операциями над векторами называются операции сложения векторов и умножения вектора на число. Так как рассматриваются линейные операции не с числами, а с новыми объектами – направленными отрезками, – то сначала мы приведем определения этих операций.
Сложение векторов
Рис. 1.4.6
Это правило сложения векторов называют правилом треугольника.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 178; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.207.115 (0.01 с.) |


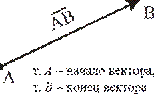

 Определение. Длиной вектора называется расстояние между началом и концом вектора.
Определение. Длиной вектора называется расстояние между началом и концом вектора.
 Определение. Нулевым или нуль-вектором называется вектор, у которого начало и конец совпадают. Обозначение: 0 (0 = 0).
Определение. Нулевым или нуль-вектором называется вектор, у которого начало и конец совпадают. Обозначение: 0 (0 = 0).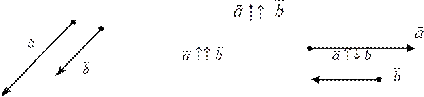
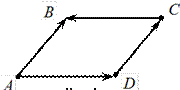



 Согласно данному определению AB = DC, но AD ¹ CB.
Согласно данному определению AB = DC, но AD ¹ CB.
 Линейные операции над векторами
Линейные операции над векторами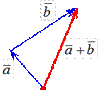
 Определение. Суммой двух векторов ā и ` b называется вектор ā +` b, идущий из начала вектора ā в конец вектора ` b при условии, что вектор` b приложен к концу вектора ā (рис. 1.4.7).
Определение. Суммой двух векторов ā и ` b называется вектор ā +` b, идущий из начала вектора ā в конец вектора ` b при условии, что вектор` b приложен к концу вектора ā (рис. 1.4.7).


