
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимое и достаточное условие коллинеарности двух векторов
Теорема. Для того, чтобы два вектора ā и ` b были коллинеарны, необходимо и достаточно, чтобы один из них мог быть представлен в виде
В этой теореме мы должны доказать два признака; один из них является необходимым для данного утверждения, а другой достаточным. Такая формулировка теоремы встречается нам впервые. Уточним, в каком случае признак называется необходимым для данного утверждения, а в каком - достаточным. Пусть имеется некоторое утверждение и какой-либо признак для проверки справедливости этого утверждения. Если из справедливости данного утверждения следует выполнение признака, то такой признак называется необходимым для данного утверждения. Если же наоборот – из выполнения признака следует справедливость данного утверждения, то такой признак называется достаточным для данного утверждения. Признак может быть только необходимым, или только достаточным, или одновременно и достаточным, и необходимым. ► Доказательство теоремы разобьем на две части. i) Докажем необходимость. Если один из векторов, например, ` b =`0, то ` b = 0· ā = l ā (при l = 0) и теорема доказана).
a 0 = 1 a, b 0 = 1 b.
Обозначив =l, получим ` b = l ā. Заметим, что в этом случае l > 0.
b =- или b =- . Обозначив - = l, получим ` b = l ā.
ii) Докажем достаточность. Пусть даны два вектора ā и` b, и известно, что существует число l такое, что` b = l ā. Надо доказать, что ā ||` b. Доказательство этого утверждения немедленно следует из определения умножения вектора на число. ◄
1.4.4. Напомним, что любые два вектора можно считать лежащими в одной плоскости.
► Доказательство. Рис. 1.4.12 1) Докажем возможность (существование) такого разложения. Приведем векторы ā и ` b к общему началу O. Рассмотрим произвольный вектор` с, лежащий в этой плоскости. Приложим его к точке O. (рис. 1.4.12). Построим параллелограмм OABC, стороны которого параллельны векторам ā и` b, а вектор` с является диагональю этого параллелограмма.
2) Докажем единственность разложения. Покажем, что числа x и y для каждого вектора` с определяются единственным образом.
Допустим, что существуют числа x 1 и y 1 такие, что c = x 1 a + y 1 b, причем
   справедливо хотя бы одно из неравенств x ¹ x 1, y ¹ y 1. Тогда справедливо хотя бы одно из неравенств x ¹ x 1, y ¹ y 1. Тогда
xa + yb = x 1 a + y 1 b или (x - x 1 )a = (y 1 - y)b. Предположим, что x ¹ x 1, тогда a = y 1 - y b.
Если обозначить y 1 - y = l, то a =l b, значит векторы ā и ` b коллинеарны
в силу достаточного условия коллинеарности векторов, что противоречит условию теоремы (ā и` b не коллинеарны). Значит предположение о существовании другого разложения вектора` с по векторам ā и` b неверно, следовательно, такое разложение единственно. ◄. В связи с этой теоремой дадим следующее определение. Определение. Базисом на плоскости называются любые два неколлинеарных вектора.
Используя понятие базиса, доказанную теорему можно сформулировать следующим образом. В доказанной выше теореме базисными векторами являются векторы ā
и` b.
1.4.5. Пусть ā,` b,` с – три некомпланарных вектора. Разложить вектор ` d по векторам ā,` b и` с – значит представить
Теорема. Любой вектор` d в пространстве можно разложить по трем некомпланарным векторам ā,` b и` с, и такое разложение единственно. ► Доказательство этой теоремы аналогично доказательству предыдущей теоремы, только в данном случае нужно построить параллелепипед, ребра которого параллельны векторам ā,` b и` с, а вектор` d является диагональю этого параллелепипеда.
Рис. 1.4.13
d = OD + OC, OD = OA + OB,, т.е. d = OA + OB + OÑ,
, тогда по
, Таким образом получается разложение: d некоторые числа (рис. 1.4.13). = xa + yb + zc, где x, y и z – Единственность этого разложения доказывается методом от противного, аналогично тому, как это сделано в предыдущей теореме. Предлагается сделать это самостоятельно. ◄ Определение. Базисом в пространстве называются любые три некомпланарных вектора.
Доказанную теорему можно сформулировать следующим образом. В приведенной теореме базисными векторами являются векторы ā,` b и` с. Замечание. Базис на плоскости и в пространстве можно выбрать бесконечным числом способов.
ЛЕКЦИЯ 2 ТЕМА 1.5. Векторная алгебра. Скалярное, векторное и смешанное произведения векторов; их определения, основные свойства, способы вычисления и применения к решению геометрических и физических задач (задача о работе силы, о моменте силы). 1.5.1. Проекция вектора на ось. 1.5.2. Векторы в прямоугольной системе координат. 1.5.3. Скалярное произведение двух векторов, определение, свойства, физический смысл скалярного произведения: задача о работе силы. Вычисление скалярного произведения в прямоугольной системе координат. Направляющие косинусы вектора. 1.5.4. Векторное произведение векторов. Тройки векторов. Векторное произведение: определение, свойства, физический смысл: задача о моменте силы. Вычисление векторного произведение в прямоугольной системе координат. 1.5.5 Смешанное (векторно-скалярное) произведение трех векторов: определение, свойства. Вычисления смешанного произведения в прямоугольной системе координат.
1.5.1.
На рис.1.5.1, 1.5.2 вектор ` l 0 – орт оси l, т.е. единичный вектор, сонаправленный с осью.
Определение. Вектор A 1 B 1, идущий из проекции начала в проекцию конца
Обозначение: A 1 B 1 = сост l AB.
пр l AB = , на рис. 2:
пр l AB =-.
l 0 (направление компоненты совпадает с направлением оси),
Если
(направление компоненты противоположно направлению оси), то
A 1 B 1 = -
× l 0 = пр l AB × l 0 (рис. 1.5.2).
 Вывод: компонента вектора по оси всегда равна произведению орта оси на проекцию вектора эту ось: Вывод: компонента вектора по оси всегда равна произведению орта оси на проекцию вектора эту ось:
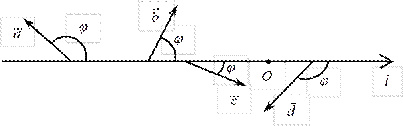
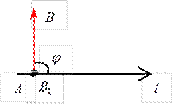
Определение. Углом наклона вектора к оси называется наименьший из углов, которые образует вектор с положительным направлением оси (рис.3).
Рис. 1.5.3 На приведенных рисунках угол наклона вектора к оси обозначен буквой j (очевидно, что 0 ≤ j ≤ p).
► Доказательство. Рассмотрим отдельно случаи: а) угол наклона вектора к оси острый, б) угол наклона вектора к оси тупой, в) вектор перпендикулярен к оси.
а) Пусть 0 £ j < p 2 Рис. 1.5.4 (рис.4), тогда из D ABB 1:
б) Пусть Рис. 1.5.5 p < j £ p (рис 5), тогда из D ABB 1: 2
пр l AB = - = -( × cos(p - j)), т.е. пр l AB = -( × (-cos j)) = × cos j
в) Пусть j = p 2
(рис.6), тогда Рис. 1.5.6

Замечание. Это свойство с помощью обычной индукции легко распространить на сумму любого конечного числа векторов.
1.5.2.
Векторы i, j,k – некомпланарны, поэтому любой вектор ā можно
i, j, k, то есть представить в виде a = xi + yj + zk, где
Эти числа называются прямоугольными координатами вектора ā. Геометрический смысл прямоугольных координат вектора.
вектора по базису i, j, k: OA = x i; OB = y j; OC = zk.
Векторы OA, OB, OC являются компонентами вектора ā по
  Теорема. Прямоугольные координаты любого вектора равны проекциями этого вектора на координатные оси: Теорема. Прямоугольные координаты любого вектора равны проекциями этого вектора на координатные оси:
Замечание. Доказанная теорема приводит к простому удобному следствию: всякий вектор можно записать и в виде разложения по компонентам a = xi + yj + zk, и – короче – в виде строки его координат ā = (x, y, z).
i = (1,0,0),
j = (0,1,0), k = (0,0,1).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 529; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.185.147 (0.127 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 произведения некоторого числа на другой вектор, т. е. b = l a (или a = l b).
произведения некоторого числа на другой вектор, т. е. b = l a (или a = l b).

 Пусть векторы ā и ` b коллинеарны, ā ¹ 0 и` b ¹ 0. Докажем, что существует действительное число l такое, что ` b = l ā.
Пусть векторы ā и ` b коллинеарны, ā ¹ 0 и` b ¹ 0. Докажем, что существует действительное число l такое, что ` b = l ā.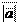
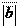
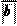 а) Если векторы ā и` b сонаправлены, то ā 0 =` b 0, т. е. b
а) Если векторы ā и` b сонаправлены, то ā 0 =` b 0, т. е. b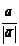

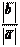

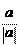
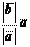
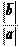 б) Если векторы ā и` b направлены противоположно, то ā 0 = –` b 0, т. е.
б) Если векторы ā и` b направлены противоположно, то ā 0 = –` b 0, т. е.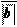 Заметим, что в этом случае l < 0. Таким образом, если векторы ā и` b коллинеарны, то` b = l ā.
Заметим, что в этом случае l < 0. Таким образом, если векторы ā и` b коллинеарны, то` b = l ā. Разложение вектора на плоскости по двум неколлинеарным векторам
Разложение вектора на плоскости по двум неколлинеарным векторам
 Разложить вектор ` с на плоскости по двум неколлинеарным векторам ā и ` b – значит представить вектор ` с в виде cуммы c = xa + yb, где x и y – некоторые числа.
Разложить вектор ` с на плоскости по двум неколлинеарным векторам ā и ` b – значит представить вектор ` с в виде cуммы c = xa + yb, где x и y – некоторые числа.

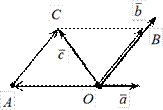





 По правилу параллелограмма: c = OA + OB. Вектор , тогда по необходимому условию коллинеарности: OA = xa . Вектор , тогда по необходимому условию коллинеарности: OB = y b.
По правилу параллелограмма: c = OA + OB. Вектор , тогда по необходимому условию коллинеарности: OA = xa . Вектор , тогда по необходимому условию коллинеарности: OB = y b.
 Получаем: c = xa + yb, где x, y – некоторые числа, и возможность разложения вектора ` c по векторам ā и` b доказана.
Получаем: c = xa + yb, где x, y – некоторые числа, и возможность разложения вектора ` c по векторам ā и` b доказана.

 x - x 1
x - x 1
 x - x 1
x - x 1
 Разложение вектора в пространстве по трем некомпланарным векторам
Разложение вектора в пространстве по трем некомпланарным векторам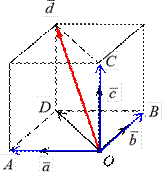





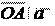

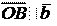

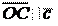



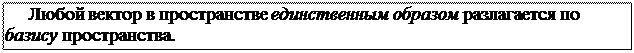
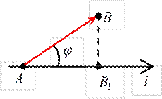
 Задана некоторая ось l (прямая с выбранным на ней направлением, началом отсчета и масштабом измерения) и вектор AB.
Задана некоторая ось l (прямая с выбранным на ней направлением, началом отсчета и масштабом измерения) и вектор AB.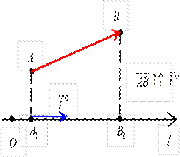
 Из точек A и B опускаются перпендикуляры на ось l, через точку A 1 обозначим проекцию точки A (начала вектора), через B – проекцию точки B (конца вектора AB).
Из точек A и B опускаются перпендикуляры на ось l, через точку A 1 обозначим проекцию точки A (начала вектора), через B – проекцию точки B (конца вектора AB).



 вектора AB называется компонентой (или составляющей) вектора AB по оси l.
вектора AB называется компонентой (или составляющей) вектора AB по оси l.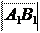 Определение. Проекцией вектора на ось называется число, равное модулю компоненты этого вектора, взятое со знаком плюс, если направление компоненты совпадает с направлением оси, и со знаком минус, если направление компоненты противоположно направлению оси.
Определение. Проекцией вектора на ось называется число, равное модулю компоненты этого вектора, взятое со знаком плюс, если направление компоненты совпадает с направлением оси, и со знаком минус, если направление компоненты противоположно направлению оси. Обозначается проекция вектора AB на ось l:
Обозначается проекция вектора AB на ось l: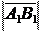 пр l AB =±.
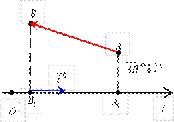
пр l AB =±.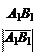 На рис. 1:
На рис. 1:
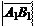 Если
Если

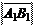 A 1 B 1 ¯ l 0
A 1 B 1 ¯ l 0
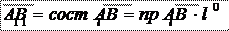
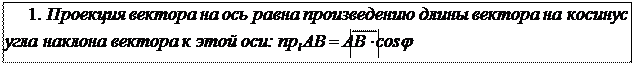


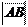 пр l AB = = ×cos j.
пр l AB = = ×cos j.

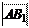
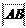
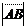
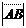

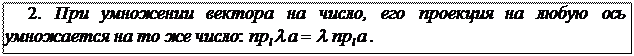
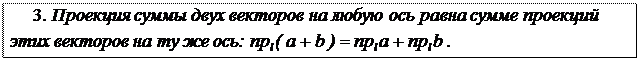
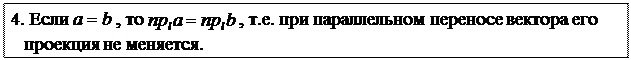




 Пусть в пространстве задана прямоугольная декартова система координат (ПДСК), т.е. три взаимно перпендикулярных оси: ось OX – ось абсцисс, ось OY – ось ординат, ось OZ – ось аппликат. На каждой из осей возьмем единичный вектор (орт оси): вектор i – по оси OX; вектор j – по оси OY; вектор k – по оси OZ. Направление осей выбрано согласно рис. 1.5.7.
Пусть в пространстве задана прямоугольная декартова система координат (ПДСК), т.е. три взаимно перпендикулярных оси: ось OX – ось абсцисс, ось OY – ось ординат, ось OZ – ось аппликат. На каждой из осей возьмем единичный вектор (орт оси): вектор i – по оси OX; вектор j – по оси OY; вектор k – по оси OZ. Направление осей выбрано согласно рис. 1.5.7.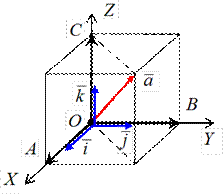









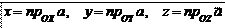
 Замечание. В частности, орты координатных осей имеют координаты:
Замечание. В частности, орты координатных осей имеют координаты:



