Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекционный (теоретический) материал по математикеСтр 1 из 29Следующая ⇒
ЛЕКЦИОННЫЙ (ТЕОРЕТИЧЕСКИЙ) МАТЕРИАЛ ПО МАТЕМАТИКЕ ЛИТЕРАТУРА 1. Самохин М.В., Каган М.Л. Математика в инженерном вузе. Алгебра и геометрия, М., Стройиздат. 2003г. 2. Письменный, Д. Т. Конспект лекций по высшей математике. Полный курс [Текст] / Д. Т. Письменный. - 11-е изд. - Москва: Айрис-пресс, 2013. - 603 с.: ил., табл. - (Высшее образование). - ISBN 978-5-8112-4866-7. 3. Каган, М. Л. Математика в строительном вузе. Дифференциальное исчисление [Текст]: [учебник для вузов] / М. Л. Каган, М. В. Самохин; [рец.: А. В. Чечкин, Ю. Ю. Кочетков]. - М.: Изд-во АСВ, 2012. - 242 с. 4. Кузина Т.С., Фриштер Л.Ю. Высшая математика. Лекции (1 семестр). М., НИУ МГСУ, 2014, 69 стр. 5. Клетеник, Д. В. Сборник задач по аналитической геометрии [Электронный ресурс]: учебное пособие / Д. В. Клетеник. - изд. 17-е стереотип. - Электрон. текстовые дан. - Санкт-Петербург: Лань, 2019. - (Договор №04-НТБ/19). - ISBN 978-5-8114-1051-4: www.e.lanbook.ru. 6. Берман Г.Н. Сборник задач и упражнений по математическому анализу, 17-е издание. М., Профессия, 2006г.
ЛЕКЦИЯ 1 ТЕМА 1.4. ВЕКТОРНАЯ АЛГЕБРА. Линейные Сложение векторов
Рис. 1.4.6
Это правило сложения векторов называют правилом треугольника.
Умножение вектора на число Пусть дан вектор ā и действительное число l, | ā | – длина вектора ā, |l| – абсолютная величина (модуль) числа l (лямбда). Определение. Произведением вектора ā на число l называется вектор l ā (или ā l), обладающий следующими свойствами: 1) длина вектора l ā равна произведению длины вектора ā на абсолютную величину числа l, т. е. |l ā | = |l|| ā |; 2)вектор l ā коллинеарен вектору ā (l ā || ā), причем, если l > 0, то l ā ↑↑ ā; если l < 0, то l ā ↑↓ ā; если l = 0, то l ā = 0. Замечание. При умножении вектора на l = –1 его длина не изменяется, а направление меняется на противоположное, поэтому вектор – ā называется противоположным вектору ā. Свойства линейных операций над векторами 1)
сомножителя относительно суммы чисел).
Докажите это свойство самостоятельно, используя определения линейных операций над векторами, рассмотрев два случая: l1 и l2 имеют одинаковые знаки, l1 и l2 имеют различные знаки. 2)
относительно суммы векторов).
3)
Разность двух векторов.
Рис. 1.4.10 Определение. Разностью двух векторов ā и` b называется вектор ā –` b, который в сумме с вектором` b дает вектор ā (рис. 1.4.10). Рассмотрим векторы ā и` b. Приведем их к общему началу O. Обозначим:
Рис. 1.4.11
Определение. Единичным вектором называется вектор, длина которого равна единице, т.е. | ā | = 1. Определение. Орт вектора ā – это единичный вектор, сонаправленный с вектором ā. Орт вектора ā обозначается ā 0 (ā 0 ↑↑ ā, | ā 0| = 1).
a 0 = 1 a.
ЛЕКЦИЯ 2 ТЕМА 1.5. Векторная алгебра. Скалярное, векторное и смешанное произведения векторов; их определения, основные свойства, способы вычисления и применения к решению геометрических и физических задач (задача о работе силы, о моменте силы). 1.5.1. Проекция вектора на ось. 1.5.2. Векторы в прямоугольной системе координат. 1.5.3. Скалярное произведение двух векторов, определение, свойства, физический смысл скалярного произведения: задача о работе силы. Вычисление скалярного произведения в прямоугольной системе координат. Направляющие косинусы вектора. 1.5.4. Векторное произведение векторов. Тройки векторов. Векторное произведение: определение, свойства, физический
смысл: задача о моменте силы. Вычисление векторного произведение в прямоугольной системе координат. 1.5.5 Смешанное (векторно-скалярное) произведение трех векторов: определение, свойства. Вычисления смешанного произведения в прямоугольной системе координат.
1.5.1.
На рис.1.5.1, 1.5.2 вектор ` l 0 – орт оси l, т.е. единичный вектор, сонаправленный с осью.
Определение. Вектор A 1 B 1, идущий из проекции начала в проекцию конца
Обозначение: A 1 B 1 = сост l AB.
пр l AB = , на рис. 2:
пр l AB =-.
l 0 (направление компоненты совпадает с направлением оси),
Если
(направление компоненты противоположно направлению оси), то
A 1 B 1 = -
× l 0 = пр l AB × l 0 (рис. 1.5.2).
 Вывод: компонента вектора по оси всегда равна произведению орта оси на проекцию вектора эту ось: Вывод: компонента вектора по оси всегда равна произведению орта оси на проекцию вектора эту ось:
Определение. Углом наклона вектора к оси называется наименьший из углов, которые образует вектор с положительным направлением оси (рис.3).
Рис. 1.5.3 На приведенных рисунках угол наклона вектора к оси обозначен буквой j (очевидно, что 0 ≤ j ≤ p).
► Доказательство. Рассмотрим отдельно случаи: а) угол наклона вектора к оси острый, б) угол наклона вектора к оси тупой, в) вектор перпендикулярен к оси.
а) Пусть 0 £ j < p 2 Рис. 1.5.4 (рис.4), тогда из D ABB 1:
б) Пусть Рис. 1.5.5 p < j £ p (рис 5), тогда из D ABB 1: 2
пр l AB = - = -( × cos(p - j)), т.е. пр l AB = -( × (-cos j)) = × cos j
в) Пусть j = p 2
(рис.6), тогда Рис. 1.5.6

Замечание. Это свойство с помощью обычной индукции легко распространить на сумму любого конечного числа векторов.
1.5.2.
Векторы i, j,k – некомпланарны, поэтому любой вектор ā можно
i, j, k, то есть представить в виде a = xi + yj + zk, где
Эти числа называются прямоугольными координатами вектора ā. Геометрический смысл прямоугольных координат вектора.
вектора по базису i, j, k: OA = x i; OB = y j; OC = zk.
Векторы OA, OB, OC являются компонентами вектора ā по
  Теорема. Прямоугольные координаты любого вектора равны проекциями этого вектора на координатные оси: Теорема. Прямоугольные координаты любого вектора равны проекциями этого вектора на координатные оси:
Замечание. Доказанная теорема приводит к простому удобному следствию: всякий вектор можно записать и в виде разложения по компонентам a = xi + yj + zk, и – короче – в виде строки его координат ā = (x, y, z).
i = (1,0,0),
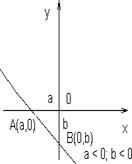
j = (0,1,0), k = (0,0,1). Уравнение прямой в отрезках
Такое уравнение называется уравнением прямой в отрезках. Рассмотрим это уравнение. Пусть x = 0, тогда y = 1,
y = b. Пусть y = 0, тогда
a x = a. Прямая проходит через точки А (а, 0) и B (0, b) (рис. 1.6.19 – рис.1.6.21).
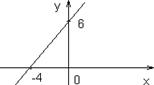
Пример. Записать уравнение прямой 3 x – 2 y + 12 = 0 в отрезках и построить эту прямую. Решение: 3 x – 2 y = –12. Разделим обе части этого уравнения на –12.
Получим: Следовательно, a = –4, b = 6.
Построим эту прямую. Для этого отложим на оси Ox a = –4, на оси Oy b = 6 и соединим полученные точки. Рис. 1.6.22
ЛЕКЦИЯ 4 Общее уравнение плоскости Уравнение
называется общим уравнением плоскости, здесь ` N = (A; B; C) – нормальный вектор.
1) Пусть D = 0. Уравнение имеет вид: Ax + By + Cz = 0. Такая плоскость проходит через начало координат.
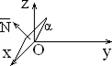
2) перпендикулярен оси Oz Þ плоскость параллельна оси Oz (рис.1.7.3)
плоскость параллельна оси Oy (рис. 1.7.4)
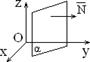
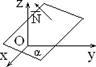
4) A = 0: By + Cz + D = 0 Þ ` N = (0; B; C) ^ Ox, плоскость параллельна оси Ox (рис. 5)
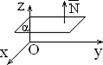
ось Oz (рис. 1.7.6) ^ Oz, плоскость проходит через
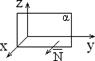
6) B = D = 0: Ax + Cz = 0 Þ ` N = (A; 0; C) ^ Oy, плоскость проходит через ось Oy (рис. 1.7.7) 7) A = D = 0: By + Cz = 0 Þ ` N = (0; B; C) ^ Ox, плоскость проходит через ось Ox (рис. 1.7.8) 8) A = B = 0: Cz + D = 0 Þ ` N = (0; 0; C) || Oz, плоскость параллельна плоскости Oxy (рис. 1.7.9)
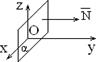
8) B = C = 0: Ax + D = 0 Þ `N = (A; 0; 0) || Ox, плоскость параллельна плоскости Oyz (рис. 1.7.10) 8) A = C = 0: By + D = 0 Þ `N = (0; B; 0) || Oy, плоскость параллельна плоскости Oxz (рис. 1.7.11)
Пример. Составить уравнение плоскости, проходящей через точку M 0(1; 2; –1) перпендикулярно вектору `N = (2; –1; 3). Найти точки пересечения этой плоскости с осями координат. Решение. По формуле (1.7.1) имеем 2(x – 1) –1·(y – 2) + 3(z + 1) =0, 2 x – y + 3 z + 3 = 0. Для того, чтобы найти пересечение этой плоскости с осью Ox, подставим в полученное уравнение y = 0, z = 0. Получим 2 x + 3 = 0; x = –1,5. Точка пересечения искомой плоскости с осью Ox имеет координаты: M 1(–1,5; 0; 0). Найдем пересечение плоскости с осью Oy. Для этого возьмем x = 0, z = 0. Имеем – y + 3 = 0 Þ y = 3. Итак, M 2(0; 3; 0). Для нахождения точки пересечения с осью Oz возьмем x = 0, y = 0. Тогда 3 z + 3 = 0 Þ z = – 1. Итак, M 3(0; 0; –1).
Ответ: 2 x – y + 3 z + 3 = 0, M 1(–1,5; 0; 0), M 2(0; 3; 0), M 3(0; 0; –1).
Пример. Исследовать плоскости, заданные уравнениями: a) 3 x – y + 2 z = 0, б) 2 x + z – 1 = 0, в) – y + 5 = 0, г) x = 0. Решение. а) Данная плоскость проходит через начало координат (D = 0) и имеет нормальный вектор `N = (3; –1; 2). б) В уравнении 2 x + z – 1 = 0 коэффициент B = 0. Следовательно, `N = (2; 0; 1). Плоскость параллельна оси Oy. в) В уравнении – y + 5 = 0 коэффициенты A = 0, C = 0. Значит, `N = (0; – 1; 0). Плоскость параллельна плоскости Oxy.
г) Уравнение x = 0 задает плоскость Oyz, так как при B = 0, C = 0 плоскость параллельна плоскости Oyz, а из условия D = 0 следует, что плоскость проходит через начало координат.
Пример. Составить уравнение плоскости, проходящей через точку A (2; 3;
Решение. Найдем вектор
BC.
–3(x – 2) + 2(y – 3) + 1·(z – 1) = 0; –3 x + 2 y + z + 6 – 6 – 1 = 0; –3 x + 2 y + z – 1 = 0; 3 x – 2 y – z + 1 = 0.
Ответ: 3 x – 2 y – z + 1 = 0. РАЗДЕЛ 2. НЕСКОЛЬКИХ ПЕРЕМЕННЫХ ЛЕКЦИЯ 5 Функция одной переменной 2.1.1.1. Функция одной переменной. Способы задания функции. 2.1.1.2. Элементы поведения функции. Ограниченные переменные величины и функции. Возрастание и убывание функции на интервале. Чѐтные и нечѐтные функции. Периодические функции. Сложная функция. 2.1.1.3. Основные элементарные функции. Элементарные функции Функция одной переменной. Или функцией. Запись y = f (x) можно понимать так: x - независимая переменная величина, y - зависимая от x переменная (то есть функция от x), а за буквой f скрывается закон соответствия, то есть обобщенная запись тех операций, которые надо проделать с аргументом x, чтобы получить соответствующие значения переменной y.
Множество D называется областью определения функции, а множество E - областью (или множеством) значений функции. Из определения функции следует, что функция является однозначной: каждому значению x ставится в соответствие одно значение y. Чтобы задать функцию надо знать область определения и закон соответствия. Способы задания функции Аналитический способ. Основным способом задания функции является аналитический способ, то есть с помощью формулы. При таком задании функции явно указаны математические операции, которые следует производить над аргументом, чтобы получить соответствующее значение функции. Например: y = 2 x 2 +1; y = sin 2 x Табличный способ. Рис. 1 Часто функция задается таблицей, в одной строке которой выписаны значения аргумента, а в другой – соответствующие им значения функции. Удобство этого способа в том, что значения функции уже известны (их не надо вычислять). Однако, известны они лишь для тех значений аргумента, которые имеются в таблице.
2.1.1. 2.1.2. Элементы поведения функции. Ограниченные переменные величины и функции. Возрастание и убывание функции на интервале. Чѐтные и нечѐтные функции. Периодические функции. Сложная функция. Элементы поведения функции. Примеры. 1). f (x) = x 2 D = (- ¥;+ ¥) f (- x) = (- x)2 = x 2 = f (x) Область определения симметрична относительно начала координат и выполняется условие f (- x) = f (x), значит это четная функция. 2). y = 1 x D: x Î(- ¥; 0)U (0; + ¥);
- x = - 1 = - y (x). x
выполняется условие y (- x) = - y (x), значит это нечетная функция. График четной функции симметричен относительно оси ординат, так как наряду с точкой M (x; f (x)) он содержит и симметричную ей относительно оси ординат точку M 1(- x; f (x)) (рис. 5).
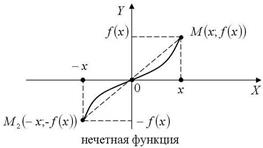
Рис. 5 График нечетной функции симметричен относительно начала координат,
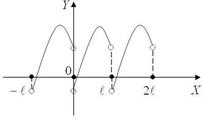
так как наряду с точкой M (x; f (x)) он содержит точку M 2 (- x; - f (x)) (рис. 6). Рис. 6 Не следует думать, что функция, не являющаяся четной, будет нечетной. Чаще всего приходится иметь дело с функциями, которые не являются ни четными, ни нечетными, их обычно называют функциями общего вида. Графики функций общего вида не обладают симметрией ни относительно оси ординат, ни относительно начала координат. Периодические функции Определение. Число l ¹ 0 называется периодом функции f (x) с областью D, если для любого x Î D f (x + l) = f (x). Это условие предполагает, что наряду с любым x, точка x +lÎ D. Функция f (x), имеющая период, называется периодической. Если l - период функции f (x), то и любое целое число, кратное l (то есть k l, где k = ±1,± 2,...), так же будет периодом f (x). Например,
то есть 2l f (x + 2l) = f ((x + l)+ l) = f (x + l) = f (x), тоже является периодом; f (x - l) = f (x - l + l) = f (x), то есть и (- l) тоже является периодом. Наиболее важным является наименьший положительный период, так как все другие периоды будут ему кратны. Поэтому в дальнейшем название периода будем применять к наименьшему положительному периоду. Факт наличия у функции периода достаточно редок. В частности периодическими являются тригонометрические функции y = sin x, y = cos x, y = tg x, y = ctg x. Для функций p . sin x и cos x - период 2 p, для функций tg x и ctg x - период График периодической функции с периодом l достаточно построить на каком-либо интервале с длиной, равной периоду, а затем построенную часть графика сдвигать вдоль оси Ox на l;- l;2l;- 2l и т.д. (рис. 7).
Рис. 7 Сложная функция Пусть дана функция y = f (u) от аргумента u, причем аргумент u, в свою очередь, является функцией от независимой переменной x: y = f (u), u = u (x). Возьмем какое-либо значение x, ему отвечает определенное значение u = u (x). Полученному значению u, в свою очередь, отвечает определенное значение y = f (u). В конечном итоге взятому значению x соответствует определенное значение y, то есть переменная y оказалась функцией независимой переменной x: y = F (x) или y = f (u (x)) = F (x) Функция F (x) называется сложной функцией от независимой переменной x или функцией от функции (функция f от функции u). Функция y = f (u) называется внешней функцией, а u = u (x) называется внутренней функцией или промежуточной переменной. Отметим, что для того, чтобы образовать функцию от функции нужно, чтобы область значений промежуточной переменной u = u (x) «укладывалась» в область определения внешней функции y = f (u). Примеры. 1) f (u) = u 2 ; u = cos x, тогда F (x) = f (u (x)) = (cos x)2; 1) f (u) = sin u; u = 3 x -1, тогда F (x) = f (u (x)) = sin(3 x -1). Полезно уметь раскладывать сложную функцию на составляющие, то есть уметь находить внешнюю функцию и промежуточную переменную (или внутреннюю функцию). Примеры. 1) y = 2 x 2; составляющие: u = x 2, f (u) = 2 u; 2)
Функция одной переменной. Элементарные функции Функции, полученные из основных элементарных функций с помощью конечного числа арифметических операций и конечного числа операций взятия функции от функции, называются элементарными.
Всякая элементарная функция может быть задана одной формулой на всей области своего определения. Например,
3 x 2 + x
, y = sin 3 æ x ö - 5 × 2- x 2
По сути дела, любая функция, закон соответствия которой задан одной формулой, является для нас элементарной, пока мы не овладеем другими знаками записи формул, кроме знаков арифметически операций и символов, которыми обозначаются основные элементарные функции.
Последовательности. Предел переменной величины. Из разнообразных способов поведения переменных величин наиболее важен такой, при котором переменная величина стремится к некоторому пределу. В этом случае значения, принимаемые переменной величиной y, становятся сколь угодно близкими к некоторому постоянному числу a - пределу этой переменной величины. Определение предела имеет простой геометрический смысл: неравенство
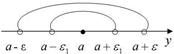
интервале (a - e, a + e) (рис. 19). Таким образом, можно дать определение предела переменной величины в геометрической форме. Число a называется пределом переменной величины y, если для любой (сколь угодно малой) e - окрестности точки a можно указать такой момент в изменении переменной y, начиная с которого все ее значения попадают в e - окрестности точки a (рис. 19 и 20).
Записывается это следующим образом a = lim y (lim - первые буквы слова limes - предел) или y ® a. Процесс приближения к пределу необходимо понимать в динамике: взяли некоторую e - окрестность точки a, начиная с некоторого момента все значения переменной y попадают в эту окрестность; теперь возьмем e 1 < e , начиная с некоторого (более отдаленного) момента все значения переменной y попадают в e 1 т.д. (рис. 20). - окрестность (меньшую по сравнению с первой) точки a и Однако, в определении предела осталась нерасшифрованной весьма существенная фраза: «начиная с некоторого момента в процессе изменения переменной величины y».
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.105.137 (0.348 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Раздел 1. ВЕКТОРНАЯ АЛГЕБРА. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Раздел 1. ВЕКТОРНАЯ АЛГЕБРА. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ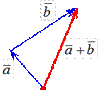
 Определение. Суммой двух векторов ā и ` b называется вектор ā +` b, идущий из начала вектора ā в конец вектора ` b при условии, что вектор` b приложен к концу вектора ā (рис. 1.4.7).
Определение. Суммой двух векторов ā и ` b называется вектор ā +` b, идущий из начала вектора ā в конец вектора ` b при условии, что вектор` b приложен к концу вектора ā (рис. 1.4.7).



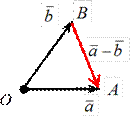






 a = OA, b = AB. Тогда, согласно данному определению: BA = a - b.
a = OA, b = AB. Тогда, согласно данному определению: BA = a - b. Разность векторов ā и` b можно рассматривать как сумму вектора ā и вектора (–` b), противоположного ` b, т.е. как ā + (–` b).
Разность векторов ā и` b можно рассматривать как сумму вектора ā и вектора (–` b), противоположного ` b, т.е. как ā + (–` b).





 Замечание. Если векторы ā и b приведены к общему началу и на них, как на сторонах, построен параллелограмм (рис. 1.4.11), то та из диагоналей этого параллелограмма, которая выходит из их общего начала, является суммой векторов: OC = a + b, а вторая диагональ BA является разностью векторов: BA a b.
Замечание. Если векторы ā и b приведены к общему началу и на них, как на сторонах, построен параллелограмм (рис. 1.4.11), то та из диагоналей этого параллелограмма, которая выходит из их общего начала, является суммой векторов: OC = a + b, а вторая диагональ BA является разностью векторов: BA a b.
 a
a Проекция вектора на ось.
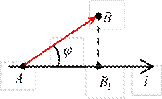
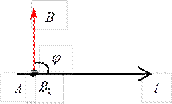
Проекция вектора на ось. Задана некоторая ось l (прямая с выбранным на ней направлением, началом отсчета и масштабом измерения) и вектор AB.
Задана некоторая ось l (прямая с выбранным на ней направлением, началом отсчета и масштабом измерения) и вектор AB.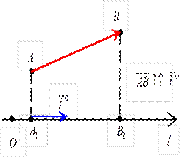
 Из точек A и B опускаются перпендикуляры на ось l, через точку A 1 обозначим проекцию точки A (начала вектора), через B – проекцию точки B (конца вектора AB).
Из точек A и B опускаются перпендикуляры на ось l, через точку A 1 обозначим проекцию точки A (начала вектора), через B – проекцию точки B (конца вектора AB).



 вектора AB называется компонентой (или составляющей) вектора AB по оси l.
вектора AB называется компонентой (или составляющей) вектора AB по оси l.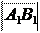 Определение. Проекцией вектора на ось называется число, равное модулю компоненты этого вектора, взятое со знаком плюс, если направление компоненты совпадает с направлением оси, и со знаком минус, если направление компоненты противоположно направлению оси.
Определение. Проекцией вектора на ось называется число, равное модулю компоненты этого вектора, взятое со знаком плюс, если направление компоненты совпадает с направлением оси, и со знаком минус, если направление компоненты противоположно направлению оси. Обозначается проекция вектора AB на ось l:
Обозначается проекция вектора AB на ось l:
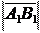 пр l AB =±.
пр l AB =±.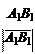 На рис. 1:
На рис. 1:
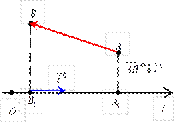
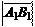 Если
Если

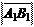 A 1 B 1 ¯ l 0
A 1 B 1 ¯ l 0
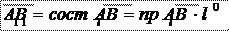
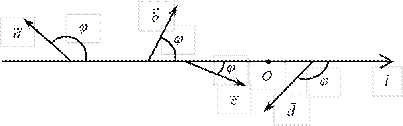
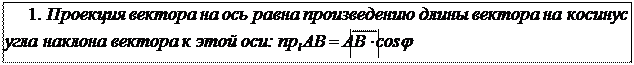


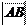 пр l AB = = ×cos j.
пр l AB = = ×cos j.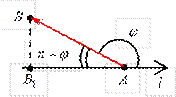

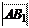
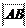
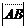
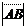



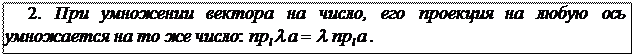
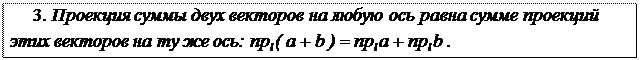
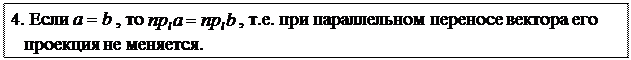






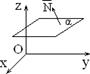
 Пусть в пространстве задана прямоугольная декартова система координат (ПДСК), т.е. три взаимно перпендикулярных оси: ось OX – ось абсцисс, ось OY – ось ординат, ось OZ – ось аппликат. На каждой из осей возьмем единичный вектор (орт оси): вектор i – по оси OX; вектор j – по оси OY; вектор k – по оси OZ. Направление осей выбрано согласно рис. 1.5.7.
Пусть в пространстве задана прямоугольная декартова система координат (ПДСК), т.е. три взаимно перпендикулярных оси: ось OX – ось абсцисс, ось OY – ось ординат, ось OZ – ось аппликат. На каждой из осей возьмем единичный вектор (орт оси): вектор i – по оси OX; вектор j – по оси OY; вектор k – по оси OZ. Направление осей выбрано согласно рис. 1.5.7.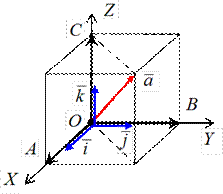









 Вектор a = OA + OB + OC (см. рис.10). В силу единственности разложения
Вектор a = OA + OB + OC (см. рис.10). В силу единственности разложения



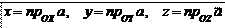

 Замечание. В частности, орты координатных осей имеют координаты:
Замечание. В частности, орты координатных осей имеют координаты:

 Если прямая отсекает на осях отрезки а и b, не равные нулю, то ее уравнение имеет вид:
Если прямая отсекает на осях отрезки а и b, не равные нулю, то ее уравнение имеет вид: b
b x = 1,
x = 1,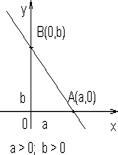


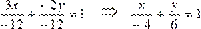

 Рассмотрим частные случаи этого уравнения.
Рассмотрим частные случаи этого уравнения.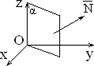
 Ее нормальный вектор N = (A, B, C).
Ее нормальный вектор N = (A, B, C). С = 0: Ax + By + D = 0 Нормальный вектор этой плоскости ` N = (A, B, 0)
С = 0: Ax + By + D = 0 Нормальный вектор этой плоскости ` N = (A, B, 0) 3) B = 0: Ax + Cz + D = 0 Þ ` N = (A, 0, C) ^ Oy,
3) B = 0: Ax + Cz + D = 0 Þ ` N = (A, 0, C) ^ Oy, 5) C = D = 0: Ax + By = 0 Þ ` N = (A, B, 0)
5) C = D = 0: Ax + By = 0 Þ ` N = (A, B, 0)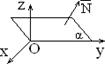
 1) и перпендикулярной вектору BC, где B (1; 0; –1), C (–2; 2; 0).
1) и перпендикулярной вектору BC, где B (1; 0; –1), C (–2; 2; 0). Вектор BC является нормальным вектором искомой плоскости, проходящей через точку A (2; 3; 1) По формуле (2.2.1) имеем:
Вектор BC является нормальным вектором искомой плоскости, проходящей через точку A (2; 3; 1) По формуле (2.2.1) имеем: y (- x) = 1
y (- x) = 1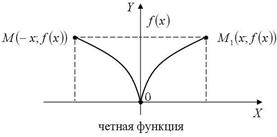
 y = log 2 (cos 2 x + 1)
y = log 2 (cos 2 x + 1)
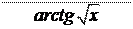


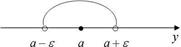
 y - a < e означает, что y находится в e - окрестности точки a, то есть в
y - a < e означает, что y находится в e - окрестности точки a, то есть в