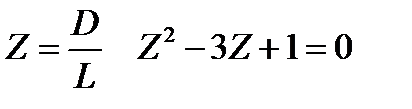Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
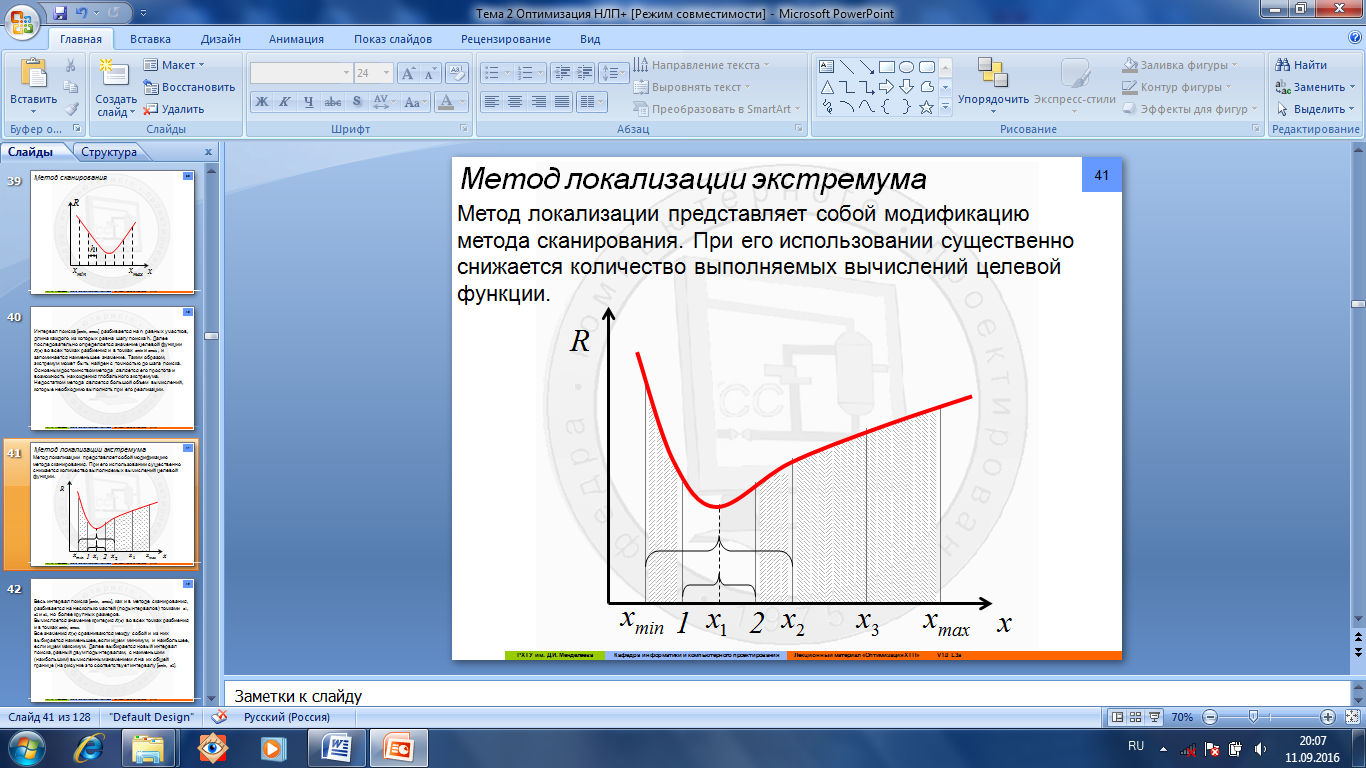
Метод локализации экстремумаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рис.1.4.9. Интервал поиска [xmin, xmax] разбивается на несколько частей Весь интервал поиска [xmin, xmax], как и в методе сканирования, разбивается на несколько частей (подынтервалов) точками x1, x2 и x3, но более крупных размеров. Вычисляется значение критерия R(x) во всех точках разбиения и в точках xmin, xmax. Все значения R(x) сравниваются между собой и из них выбирается наименьшее, если ищем минимум, и наибольшее, если ищем максимум. Далее выбирается новый интервал поиска, равный двум подынтервалам, с наименьшим (наибольшим) вычисленным значением R на их общей границе (на рисунке это соответствует интервалу [xmin, x2]. Этот интервал меньше исходного и в нем локализован экстремум. Затем поступают следующим образом. Интервал, в котором локализован экстремум, делят на несколько подынтервалов (на рисунке точками 1 и 2) и снова вычисляют значения критерия оптимальности в точках деления. Сравнивают их между собой, находят наименьшее, локализуют экстремум в меньшем интервале (на рисунке в интервале 1–2) и т.д. до тех пор, пока экстремум не будет локализован в интервале, размер которого соответствует заданной точности поиска. Наилучшие результаты поиска получаются в том случае, когда первоначальный интервал [xmin, xmax] разбивается на четыре равных поди нтервала (n = 4). При этом каждый последующий подинтервал делится пополам и вычислять значение функции нужно только в двух новых точках, так как ее значения на концах нового интервала и в его середине известны из предыдущих расчетов. Абсолютная ошибка в нахождении экстремума в этом случае определяется выражением: s – количество точек, в которых вычисляется значение критерия оптимальности.Так, при s = 21, относительная ошибка составит:
Метод Золотого сечения 1. Дан отрезок [a;b] (рис.1.4.10) на котором определена функция f(x) и точность e. Надо уточнить точку минимума с заданной точностью. Введём новое обозначение точек x1=a и x4=b и вычислим Z=(3-√5)/2. 2. Делим отрезок на три части и определяем точку x2=x1+Z(x4-x1) и точку x3=x4-Z(x4-x1). Вычисляем значения функции в этих точках F2=f(x2) F3=f(x3). 3. Определяем новый отрезок, содержащий точку экстремума, сравнив значения функций F2 и F3. Если F2 < F3, то границы нового отрезка определим как x1=x1, x4=x3, x3=x2, F3=F2 x2=x1+z(x4-x1) F2=f(x2) иначе x1=x2, x4=x4, x2=x3 F2=F3 x3=x4-z(x4-x1) 4. Проверяем условие окончания итерационного процесса | x4-x1 | £ 2e. Если оно выполняется, то определим решение, как x=(x4+x1)/2 и значение функции в этой точке f(x). Иначе перейдем на пункт 3. Введем понятие эффективности, как отношение доли сокращения отрезка к количеству вычисления функции на одной итерации тогда Q=0,3819/1≈0,3819
Рис.1.4.10. Разбиение отрезка
Заменяем Решая получим
Шаговые методы
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 471; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.120.103 (0.006 с.) |

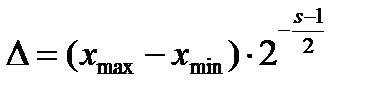
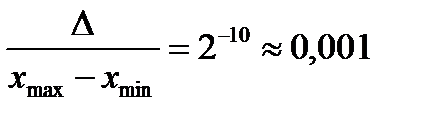

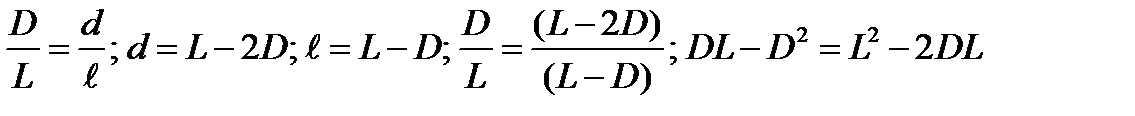 делим на
делим на