Исследование функций и экспериментальных данных численными методами, отыскание оптимальных параметров и корней

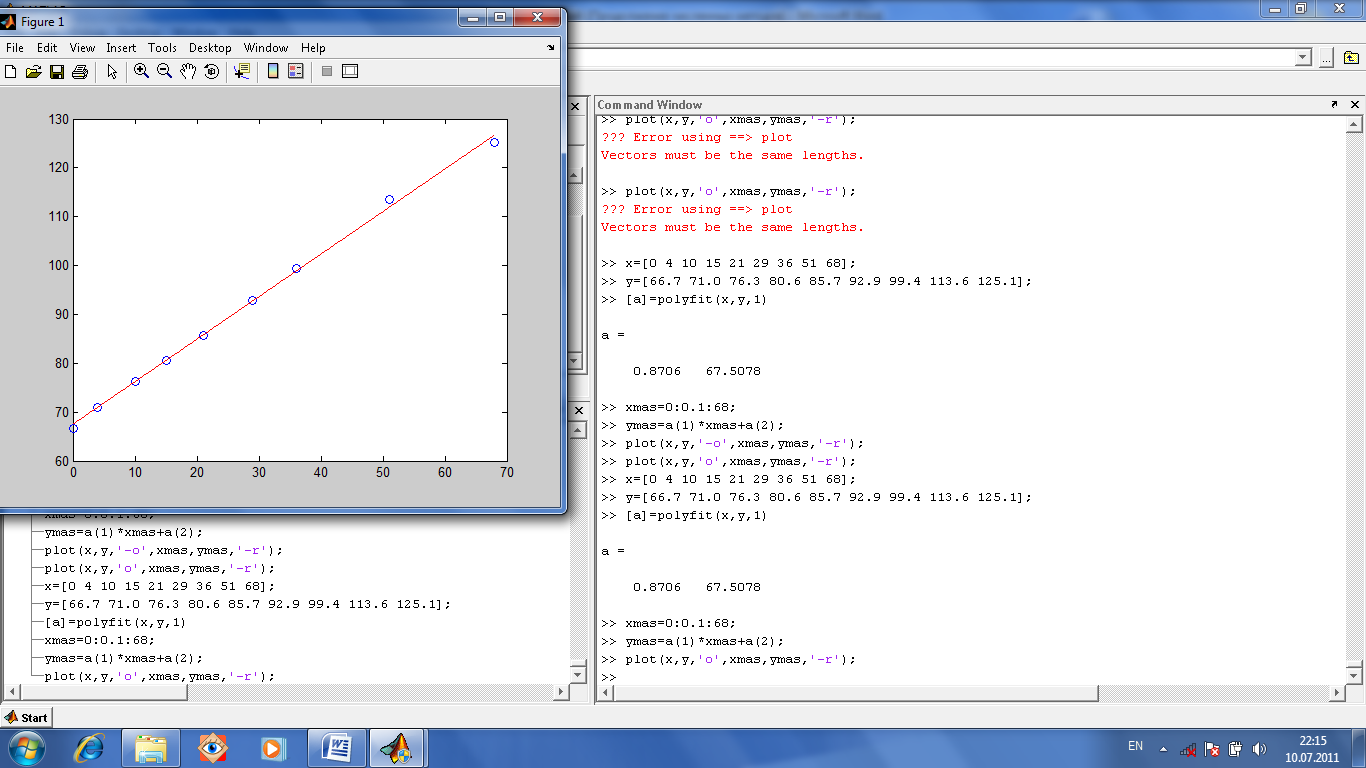
Обработка результатов эксперимента. Построение полиномиальной зависимости. Для этого есть функция polyfit, которой передаются массив абсцисс, массив ординат (экспериментальных точек) и степень полинома, который требуется получить так, чтобы он описывал экспериментальную зависимость массива ординат от массива абсцисс. Функция возвращает вектор коэффициентов вышеупомянутого полинома.

function Start_poly10 x=[0 4 10 15 21 29 36 51 68]; y=[66.7 71.0 76.3 80.6 85.7 92.9 99.4 113.6 125.1]; [a]=polyfit(x,y,1) xmas=0:0.1:68; ymas=a(1)*xmas+a(2); % дляграфика plot(x,y,'o',xmas,ymas,'-r'); end

%коэффициенты %полинома a = 0.8706 67.5078

Будет построен график (рис.1.5.1),на котором можно будет сравнить исходные точки и расчетный график. Расчетный график построен по коэффициентам полинома.

Рис.1.5.1. Исходные точки и расчетный график

Зная коэффициенты полинома, можно функцией polyval вычислить значение полинома при любом значении его аргумента (то есть получить сплошную расчетную кривую, проходящую через отдельно расположенные экспериментальные точки).

Если же требуется подобрать такую зависимость, которая не содержит некоторые степени (например, y =3 x ⁵ +6 x ³ + x +65) то тем самым требуется найти минимум функции. Поясним это на примере. Пусть требуется функция вида y = c ₁ + c ₂ x ² + c ₃ x ³, тогда, используя функцию fminsearch (‘ fname ’, c) получим вектор коэффициентов.

Однако в функцию fminsearch следует передавать не вышеописанную функцию у(х), а переделанный ее вариант вида y_i^experimental -(c ₁ + c ₂ x_i ² + c ₃ x_i ³). Тогда минимум функции будет достигнут в случае, если вычисленные ее значения практически совпадают с экспериментальными, то есть идеально описывают экспериментальные данные.Опишем для этого функцию exGl.

function s=exGl(c) global x; global y; s=0; for i=1:length(x)    s=s+(y(i)-c(1)-c(2)*x(i)^2-c(3)*x(i)^3)^2; end end
global x; global y; c=[2, 1, 0];	Сначала определяем вектор предполагаемых приблизительно значений с (если его неудачно выбрать то ответ не получится). Потом объявляем переменные х и у глобальными.

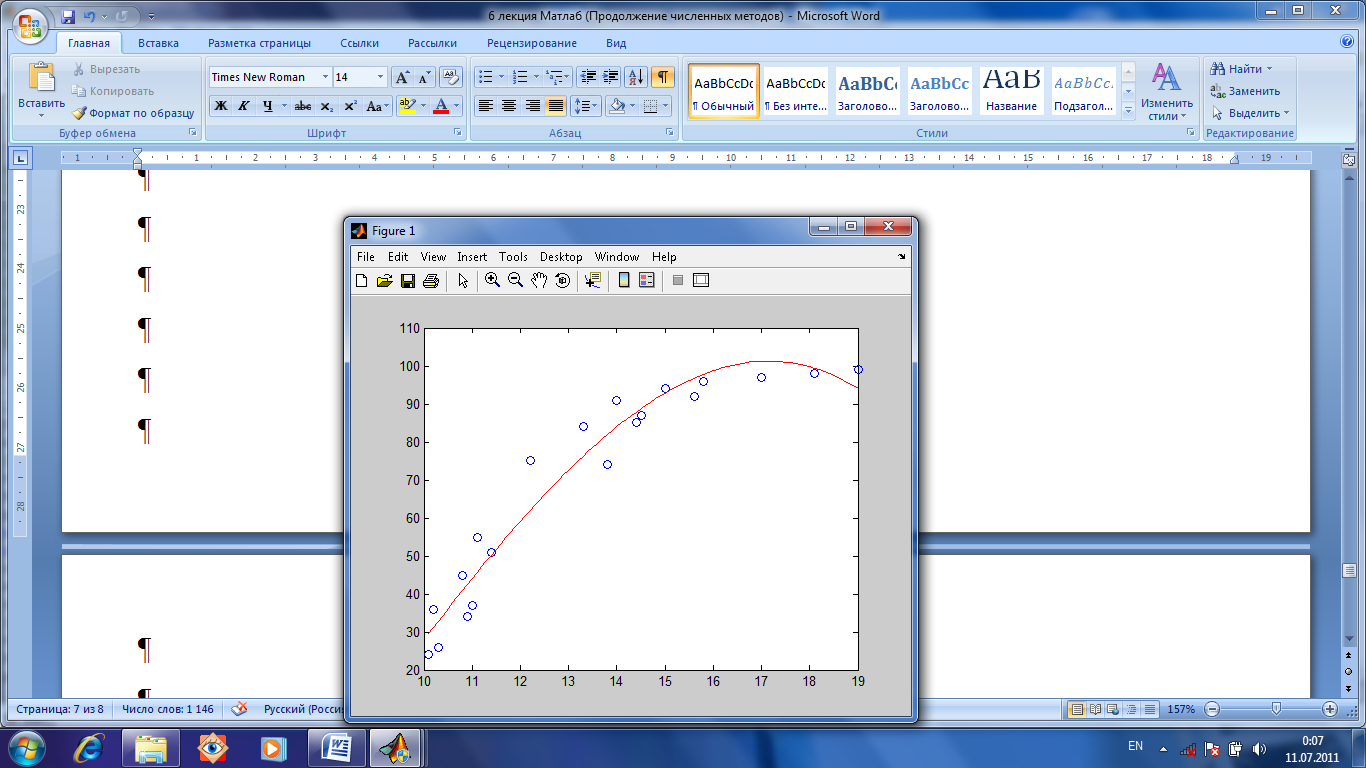
Затем вводим экспериментальные данные. После этого запускаем функцию fminsearch. Полученный от нее вектор значений с используем для построения расчетной кривой. Потом сравниваем (рис.1.5.2), насколько точно кривая идет через экспериментальные точки.

Рис.1.5.2. Сравниваем, как кривая идет через экспериментальные точки

function Start_3 x=[10.1 10.2 10.3 10.8 10.9 11 11.1 11.4 12.2 13.3 13.8 14 14.4 14.5 15 15.6 15.8 17 18.1 19]; y=[24 36 26 45 34 37 55 51 75 84 74 91 85 87 94 92 96 97 98 99];
[c,err]=fminsearch('exGl',c) t=x(1):0.1:x(length(x)); fy=c(3)*t.^3+c(2)*t.^2+c(1); plot(x,y,'o',t,fy,'r-'); end	c = -93.7295 1.9899 -0.0774 err = 754.2148

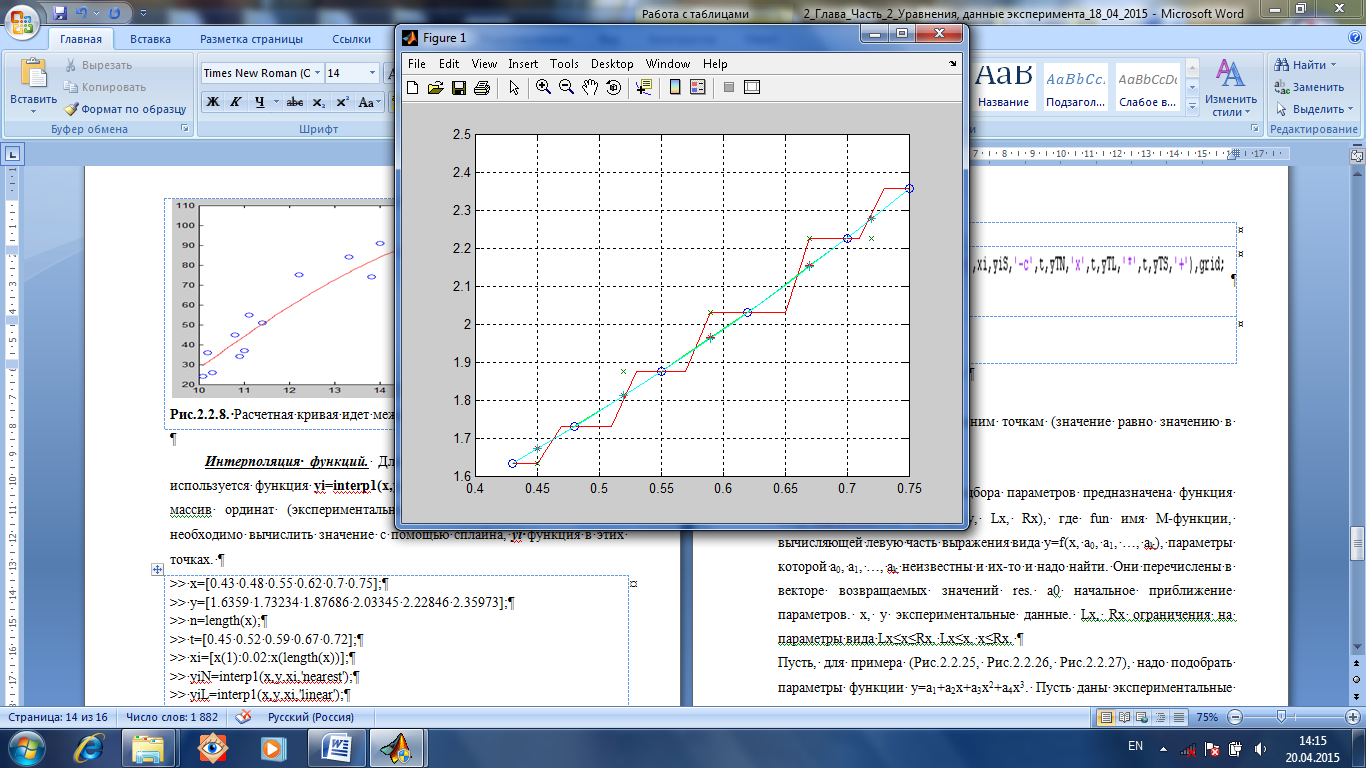
Интерполяция функций. Для реализации сплайн-интерполяции используется функция yi = interp 1(x, y, xi, method) где х массив абсцисс, у массив ординат (экспериментальных точек), xi точки, в которых необходимо вычислить значение с помощью сплайна, yi функция в этих точках. В зависимости от используемых методов, получаются различные результаты. Для уплотнения экспериментальных точек, создан массив xi из точек с одинаковым шагом, и для них будут найдены значения функции y(x). Кроме того, создан массив из точек t и эти точки расположены между экспериментальными. Для них тоже будут найдены (рис.1.5.3) значения функции y(t)

Рис.1.5.3. Интерполяция.

function Start_interp1

x=[0.43 0.48 0.55 0.62 0.7 0.75];

y=[1.6359 1.73234 1.87686 2.03345 2.22846 2.35973];

n=length(x);

t=[0.45 0.52 0.59 0.67 0.72];

xi=[x(1):0.02:x(length(x))];

yiN=interp1(x,y,xi,'nearest');

yiL=interp1(x,y,xi,'linear');

yiS=interp1(x,y,xi,'spline');

yTS=interp1(x,y,t,'spline');

yTN=interp1(x,y,t,'nearest');

yTL=interp1(x,y,t,'linear');

plot(x,y,'o',xi,yiN,'r-',xi,yiL,'g-',xi,yiS,'c-',t,yTN,'x',t,yTL,'*',t,yTS,'+');

grid on;

end

linear линейнаяинтерполяция;

spline кубический сплайн;

nearest интерполяция по соседним точкам (значение равно значению в ближайшей узловой точке).

Подбор параметров. Для подбора параметров предназначена функция [ res ]= lsqcurvefit (fun, a 0, x, y, Lx, Rx), где fun имя М-функции, вычисляющей левую часть выражения вида y = f (x, a ₀, a ₁, …, a_k), параметры которой a ₀, a ₁, …, a_k неизвестны и их-то и надо найти. Они перечислены в векторе возвращаемых значений res. а0 начальное приближение параметров. x, y экспериментальные данные. Lx, Rx ограничения на параметры вида Lx ≤ x ≤ Rx, Lx ≤ x, x ≤ Rx.

Пусть, для примера, надо подобрать параметры функции y = a ₁ + a ₂ x + a ₃ x ² + a ₄ x ³. Пусть даны экспериментальные данные.

Х	10.1	10.3	10.8	11	11.1	11.4	12.2	13.3	13.8	14	14.5	15	15.6	15.8	17	18.1	19
У	24	26	45	37	55	51	75	84	74	91	87	94	92	96	97	9 8	99

Выберем вектор начальных приближений а0=(2, 0, 1,0).

Опишем функцию exMnk, она вычисляет значение многочлена

function y=exMnk(a,x) y=a(1)+a(2)*x+a(3)*x.^2+a(4)*x.^3; end

Затем введем данные и построим график (рис.1.5.4) по ним.

>> X=[10.1,10.3,10.8,11,11.1,11.4,12.2,13.3,13.8,14,14.5,15,15.6,15.8,17,18.1,19]; >> Y=[24, 26, 45, 37, 55, 51, 75, 84, 74, 91, 87, 94, 92, 96, 97, 98, 99];

Рис.1.5.4. График полинома

Применим функцию lsqcurvefit(@exMNK,a0,x,y), получим коэффициенты полинома.

>> plot(x,y,'o'),grid; >> a0=[2 0 1 0]; A=lsqcurvefit(@exMnk,a0,X,Y)		Maximum number of function evaluations exceeded; increase options.MaxFunEvals A = -19.6243 -8.5171 2.0875 -0.0689
function Start_lsq x=10:0.1:19; y=exMnk(A,x); plot(X,Y,'o'),grid; hold on; plot(x,y,'r-'); end	Зададим диапазон х по горизонтальной оси и построим график функции exMnk.

Поиск экстремума функции одной переменной. При решении задач поиска максимума (минимума) выделяют локальный (с указанием границ) и глобальный максимум (минимум). Поиск (локального (в пределах определенного интервала) минимума осуществляет функция [ x, y ]= fminbnd (имяФункции,границыИнтервала).

Если же надо найти локальный максимум, то исследуемую функцию берут с другим знаком и ищут ее минимум, который фактически является ее максимумом. При этом значение функции в максимуме это найденное значение с другим знаком.

Локальный минимум функции одной переменной ищет встроенная функция [x, y]=fminbnd(name, a, b, options). В ней:

· name имя М-функции,

· a, b границы поиска,

· options параметры управляющие ходом решения,

· x, y координаты точки минимума.

Для вычисления локального максимума, надо взять функцию name с другим знаком. Для примера, рассмотрим функцию y(x)=x⁴-0.5x³-28x²+140

Сначала найдем минимум на интервале, например, от -4 до -2.

[x,y]=fminbnd(@ext,-4,-2), где @ext обращение к М-функции вычисляющей интересующую нас функцию.

Потом найдем максимум на интервале от -6 до 6, для этого обратимся не к @ext, а к @ext_2, в которой функция y(x) взята с другим знаком, то есть y(x)=-(x⁴-0.5x³-28x²+140). То есть ее минимум будет максимумом исходной функции.

Получим и в том, и в другом случае координаты точки минимума (максимума) на заданном отрезке, что и требовалось.