Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Минимальное изменение функцииСодержание книги
Поиск на нашем сайте
Если выбрано окончание процесса поиска экстремума (например, минимума) при условии, что последнее изменение функции стало меньше заданной минимальной величины, то это означает, что минимальное значение функции отличается от полученного ответа не более, чем на заданную минимальную величину. Однако, в зависимости от вида функции, тот или другой метод может быть неудобен. Например, если функция (точнее, ее график) имеет участок с очень малым наклоном, то на этом участке может быть ложное завершение поиска по условию минимального изменения функции. Если же функция (ее график) имеет минимум, расположенный между двумя участками с большим уклоном (или у края одного такого участка), то при завершении работы по минимальному изменению аргумента может быть приемлемая погрешность по аргументу, но далеко не приемлемая погрешность по функции. Поэтому необходимо заранее выбирать, как будет завершен процесс поиска экстремума. Поиск экстремума функции нескольких переменных. Если функция вычисляется от нескольких переменных, то для поиска ее минимума используется (после приблизительной оценки начальных приближений переменных в предполагаемом минимуме) команда [ x, y ]= fminsearch (имяФункции, векторНачальныхПриближенийПеременных). Минимум функции нескольких переменных z=f(x1, x2, …, xn) осуществляет встроенная функция [X,Z]=fminsearch(name, x0, options) где: · name имя М-функции вычисляющей z=f(x1, x2, …, xn), · х0 вектор из n элементов, содержащих координаты точки начального приближения, · options параметры управляющие ходом решения, · Х вектор из n элементов, содержащий значения переменных, при которых функция z=f(x1, x2, …, xn) минимальна, · Z это и есть минимальное значение функции. Например, [X, Z]=fminsearch(@extr, [3 2]); где @extr обращение к М-функции extr, вычисляющей значение интересующей нас функции z=x12+x22-6x2-2x1+11, причем заданы начальные приближения [3 2] для х1 и х2 соответственно. В результате получим значения переменных в точке минимума и значение функции в минимуме.
Решение задач линейного программирования. В задачах линейного программирования требуется найти максимум или минимум линейной функции многих переменных при линейных ограничениях в виде равенств или неравенств. Рассмотрим для примера такую задачу. Пусть функция L (x 1, x 2, x 3, x 4)= x 1 + x 2 + x 3 - x 4 и надо найти ее максимум и соответствующие ее максимуму значения переменных. Пусть даны ограничения в виде неравенств. x 1 ≥0, x 2 ≥0, x 3 ≥0, x 4 ≥0. Пусть также даны еще ограничения в виде неравенств. 3 x 1 - x 2 ≤7, x 2 -2 x 3 ≤-1, 4 x 3 - x 4 ≤3, 5 x 1 +2 x 4 ≥14. Для решения задачи линейного программирования (нахождения минимума) используется функция [ x, L, f ]= linprog (c, A, b, A 1, b 1, Lx, Rx) где x вектор значений переменных, полученный в качестве ответа; L значение функции в минимуме; f параметр, характеризующий вычислительный процесс (если он ноль то решение приостановлено после достижения максимального числа итераций, если положителен то все нормально решено, если отрицателен то решения не найдено); c функция цели представленная в виде вектора коэффициентов (в нашем случае [1 1 1 -1]), но так как нам нужен максимум, а функция [ x, L, f ]= linprog (c, A, b, A 1, b 1, Lx, Rx) ищет минимум, то в выражении для функции поменяем знак, поэтому вектор коэффициентов будет [-1 -1 -1 1]; A, b система ограничений, заданная в матричном виде Ax ≤ b (это в нашей задаче ограничения 3 x 1 - x 2 ≤7, x 2 -2 x 3 ≤-1, 4 x 3 - x 4 ≤3, 5 x 1 +2 x 4 ≥14, но так как 5 x 1 +2 x 4 ≥14 не подходит, то надо поменять знак в этом неравенстве и тогда оно будет -5 x 1 -2 x 4 ≤-14, в таком случае матрица А состоит из коэффициентов (при переменных) в этих неравенствах, а столбец b состоит из правых (не содержащих переменных) частей неравенств; A 1, b 1 система равенств вида A 1 x = b (в нашей задаче такой системы ограничений нету, но могла бы быть); Lx, Rx относятся к ограничениям в виде Lx ≤ x ≤ Rx, Lx ≤ x, x ≤ Rx (в нашей задаче есть ограничения вида Lx ≤ x, поэтому вектор Lx будет 0 0 0 0). При использовании функции linprog в списке аргументов вместо тех, которые не указаны, ставятся пустые квадратные скобки.
Рассмотрим еще пример для тренировки. Пусть дана функция W = x 1 + x 2 +3 x 3 - x 4 и надо найти ее максимум. Пусть даны ограничения в виде неравенств. x 1 -5 x 2 +4 x 3 ≤5, x 1 -2 x 2 -3 x 3 ≤4, x 1 +6 x 2 +5 x 3 ≤4, x 2 + x 3 ≤1. И пусть есть еще ограничения в виде неравенств. x 1 ≥0, x 2 ≥0, x 3 ≥0, x 4 ≥0. Решим задачу с помощью функции [ x, L, f ]= linprog (c, A, b, A 1, b 1, Lx, Rx). Для ее применения нам надо подготовить аргументы функции. Вектор с коэффициентов функции равен (1 1 3 -1), но так как функция linprog ищет минимум, а нам нужен максимум, то поменяем знак у коэффициентов функции и тогда вектор с будет (-1 -1 -3 1). Матрица А состоит из коэффициентов при переменных в системе неравенств x 1 -5 x 2 +4 x 3 ≤5, x 1 -2 x 2 -3 x 3 ≤4, x 1 +6 x 2 +5 x 3 ≤4, x 2 + x 3 ≤1. Так как все они со знаком ≤ то ничего менять не требуется. Вектор b состоит из правых частей этих же неравенств. Матрица A 1 из системы A 1х= b 1 для нас не актуальна (нет таких условий). Lx, Rx относятся к ограничениям в виде Lx ≤ x ≤ Rx, Lx ≤ x, x ≤ Rx. У нас есть ограничения в виде неравенств. x 1 ≥0, x 2 ≥0, x 3 ≥0, x 4 ≥0. Тогда вектор Lx =[0; 0; 0; 0]. Что касается остальных типов ограничений, то так как у нас нет таких ограничений, то для нас они не важны.
Задачи нелинейного программирования. Нелинейная задача отличается от линейной. В ней есть система линейных неравенств Ax ≤ b, система линейных равенств A 1 x = b 1, система ограничений вида lx ≤ x ≤ rx, lx ≤ x, x ≤ rx. Однако помимо этих уже знакомых (из линейного программирования) условий, есть еще система нелинейных ограничений вида g 1(x)≤0, и система нелинейных равенств g 2(x)=0. Для решения задачи нелинейного программирования (после выбора вектора начальных приближений х0) используется функция [ x, y, f ]= fmincon (F, x 0, A, b, A 1, b 1, Lx, Rx, G), где F это M-функция exNotLinear, G это М-функция exGNotLinear, вычисляющая левые части нелинейных ограничений g 1(x)≤0, g 2(x)=0. Если какие-то аргументы не определены, то вместо них в вызове функции ставятся квадратные скобки. Рассмотрим для примера следующую задачу. Пусть дана функция x 1 2 + x 2 2 =1 при условии, что x 1 x 2 =4, x 1 ≥0, x 2 ≥0. Вектор начальных приближений примем равным х0=(0.1, 0.1). Опишем функции exGNotLinear и exNotLinear.
Применим функцию [x, y, f]=fmincon(F, x0, A, b, A1, b1, Lx, Rx, G).
Пример 3 Найти минимум функции
При ограничениях: В пакете MatLab для определения минимума с начальными приближениями: x 0 = [3.5, 0.2, 3.5] используется функция fmincon, которая записывается
Экстремум функции n переменных с m ограничениями (условиями) в виде равенств:
уравнения математического описания
В полученной функции переменные являются независимыми.
определяются значения
Необходимое условие существования экстремума функции многих переменных:
поскольку
со значениями из предыдущей системы уравнений Для равенства последнего выражения 0 необходимо, чтобы каждое слагаемое его было равно 0:
Одновременно должны выполняться m равенств, соответствующих ограничениям задачи:
Функция Лагранжа Ф
по всем (i=1,…n) и (j=1,…m) приводят к требуемой системе
Получим требуемую систему (n+m) уравнений: сведя задачу к нахождению безусловного экстремума функции Ф.
ПРИМЕР 1. Классическая задача.
Записываем функцию Лагранжа:
Дифференцируя, получим:
Решая систему уравнений:
ПРИМЕР 2. Оптимальное распределениепотока сырья между параллельно работающими аппаратами Пусть общий поток (расход) сырья v, содержащий компонент A, распределяется (рис.1.6.1) между N аппаратами. Пусть Ri = Ri (vi) есть критерий оптимальности i -го аппарата и является функцией потока vi, проходящего через этот аппарат.
оптимальности записывается как: Ограничение в виде равенства имеет вид:
производные, получим систему (N +1)
и :
должны выполняться равенства:
Задача 2
Рис.1.6.2. Поток сырья поступает на параллельные реакторы В качестве критерия оптимальности использовать суммарное количество компонента P в выходном потоке. Исходные данные для расчёта: число аппаратов N = 3 объёмы аппаратов, соответственно: 0,5, 0,6, 0,7 м 3 расход сырья v = 3 м 3/ час условия работы аппаратов - изотермические константы скоростей k 1 = 0,65 1/ час; k 2 = 0,3 1/ час Решение
Уравнение ограничений на процесс:
При оптимальных условиях должны выполняться равенства:
Вычислим значение производной:
Тогда:
то будет справедливо:
Получаем систему уравнений для расчёта распределения потоков:
Подставляя исходные данные, получим:
ПРИМЕР 3. Оптимизация многостадийных процессов
конечных уравнений вида: i – номер стадии, k – номер переменной
Рис.1.6.3. Многостадийный процесс
Уравнения математической модели могут быть записаны в неявной форме:
и могут рассматриваться как уравнения ограничений.
Составим функцию Лагранжа:
по
Для нахождения оптимума полученная система из трёх последних систем уравнений должна решаться совместно с уравнениями математической модели, которые получаются при дифференцировании по Лямбда λ в соответствии с рассматриваемым методом Лагранжа.
Задача 4 Для заданного числа реакторов в каскаде N = 3 и заданной степени превращения реагента A χ AN = 0,936 реакции первого порядка типа A → P найти такое распределение объёмов реакторов Vi, при котором их суммарный объём V был бы минимальным. Условия работы каскада реакторов изотермические; значение константы скорости k = 0,35 час-1, объёмный расход v = 2 м3/час.
Уравнение, соответствующее
Обозначим долю непревращенного реагента A на выходе из каскада реакторов:
N – число аппаратов в каскаде Уравнение ограничений принимает вид:
баланса для i -го реактора:
получим: Критерий оптимальности будет иметь вид:
Запишем функцию Лагранжа:
или
Это означает, что:
одинаковым и равным
По условию η 0 = 0,064, тогда
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 165; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.211.190 (0.008 с.) |

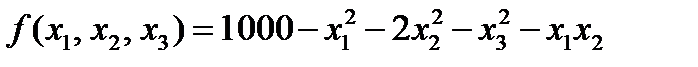

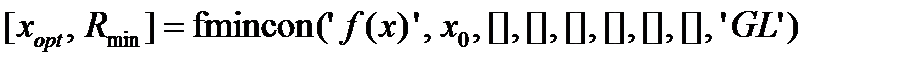 m-файл функции ограничений MatLab имеет вид
m-файл функции ограничений MatLab имеет вид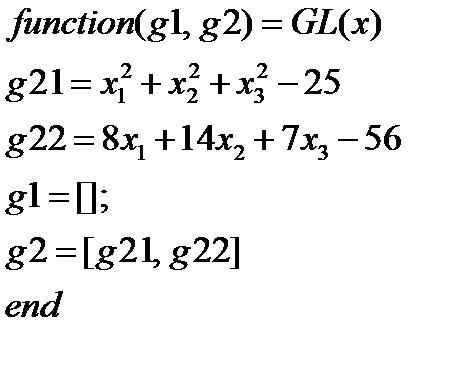 Результат
Результат 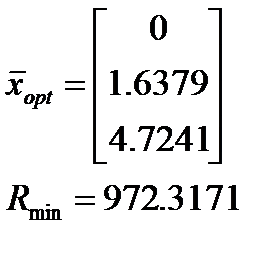
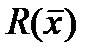 1.6. Понятие условного экстремума
1.6. Понятие условного экстремума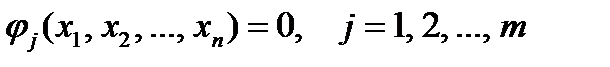
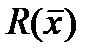 называется условным экстремумом.
называется условным экстремумом.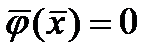 При решении задач оптимизации ХТП критерий оптимальности
При решении задач оптимизации ХТП критерий оптимальности Для такой постановки задачи определения условного экстремума необходимо выполнение условия:
Для такой постановки задачи определения условного экстремума необходимо выполнение условия: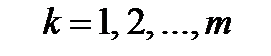
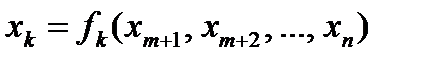 Для определения условного экстремума целесообразно выразить m зависимых переменных через остальные n – m переменных:
Для определения условного экстремума целесообразно выразить m зависимых переменных через остальные n – m переменных: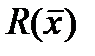
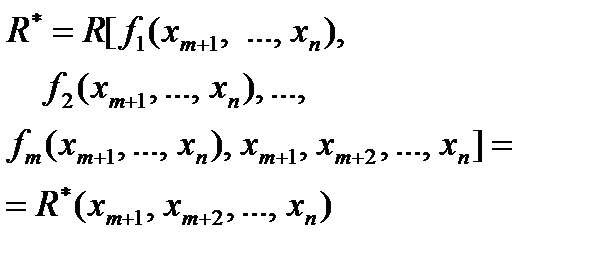 Полученные зависимости подставляются в выражение функции :
Полученные зависимости подставляются в выражение функции :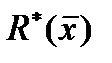
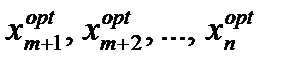
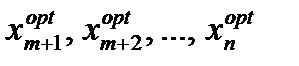 т. е. находится экстремум функции
т. е. находится экстремум функции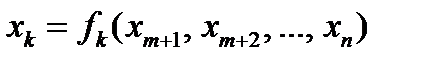 По известным значениям
По известным значениям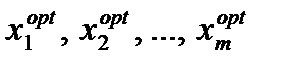 из соотношений
из соотношений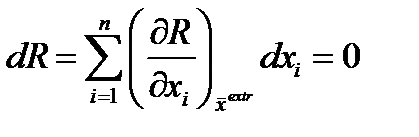 Метод неопределенных множителей Лагранжа
Метод неопределенных множителей Лагранжа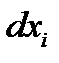
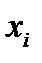 В случае условного экстремума не все дифференциалы
В случае условного экстремума не все дифференциалы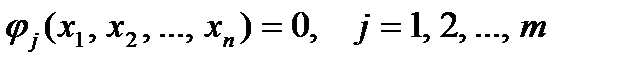 будут независимыми, т.к. на переменные наложены дополнительные ограничения
будут независимыми, т.к. на переменные наложены дополнительные ограничения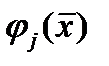
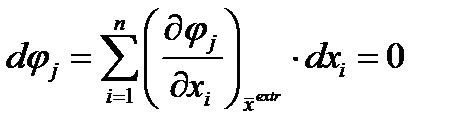 Полный дифференциал функции в точке экстремума равен нулю:
Полный дифференциал функции в точке экстремума равен нулю: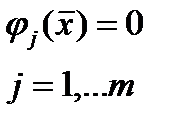
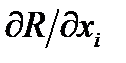
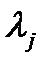 Умножив обе части последнего выражения на некоторый множитель
Умножив обе части последнего выражения на некоторый множитель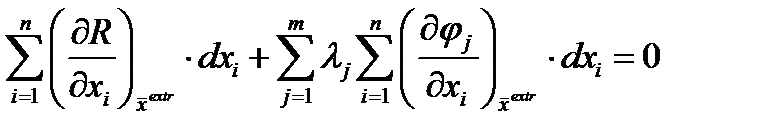 (j=1,…m), просуммировав и сложив с выражением для , получим:
(j=1,…m), просуммировав и сложив с выражением для , получим: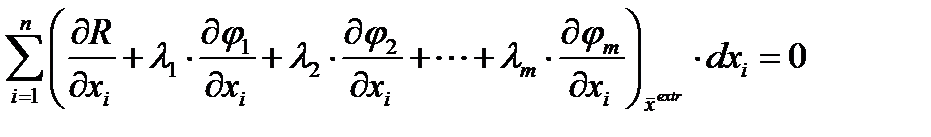 или
или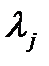 Исключим m зависимых дифференциалов таким выбором
Исключим m зависимых дифференциалов таким выбором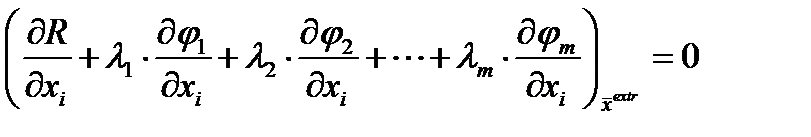 множителей , чтобы коэффициенты при зависимых дифференциалах обратились в 0:
множителей , чтобы коэффициенты при зависимых дифференциалах обратились в 0: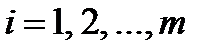
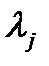 Полученная система из m уравнений позволяет определить m множителей (если они существуют)
Полученная система из m уравнений позволяет определить m множителей (если они существуют)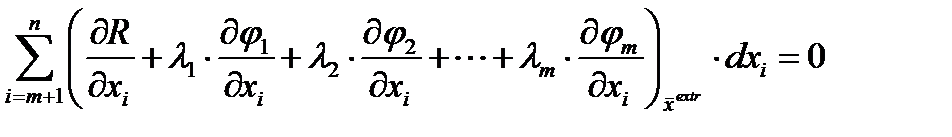 Исключив зависимые дифференциалы, получим:
Исключив зависимые дифференциалы, получим: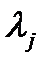
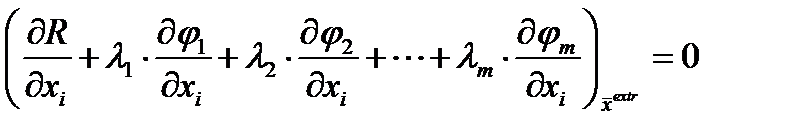
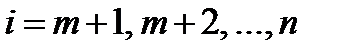
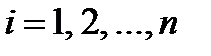
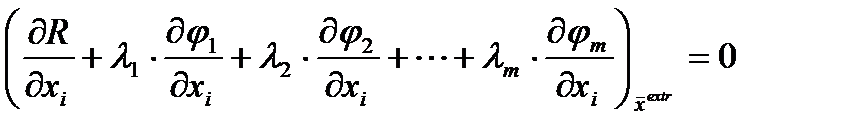 Объединяя условия равенства 0 зависимых и независимых дифференциалов, получим:
Объединяя условия равенства 0 зависимых и независимых дифференциалов, получим: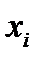
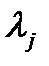 Таким образом, для определения экстремума функции Rc ограничениями типа равенств необходимо решить требуемую систему (n+m) последних уравнений относительно (i=1,…n) и (j=1,…m)
Таким образом, для определения экстремума функции Rc ограничениями типа равенств необходимо решить требуемую систему (n+m) последних уравнений относительно (i=1,…n) и (j=1,…m)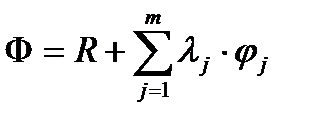
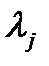
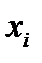 Введя функцию Лагранжа Ф, необходимые условия экстремума которой с производными
Введя функцию Лагранжа Ф, необходимые условия экстремума которой с производными  (n+m) уравнений:
(n+m) уравнений: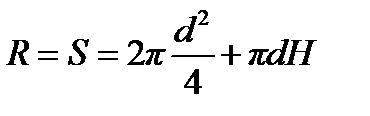 Определим соотношение между высотой и диаметром цилиндрического сосуда при минимальной его поверхности и заданном объёме.Для этого случая:
Определим соотношение между высотой и диаметром цилиндрического сосуда при минимальной его поверхности и заданном объёме.Для этого случая: S – поверхность цилиндра, H – высота цилиндра, d – диаметр цилиндра
S – поверхность цилиндра, H – высота цилиндра, d – диаметр цилиндра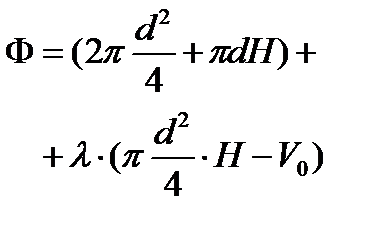 V0 – заданный объём цилиндра
V0 – заданный объём цилиндра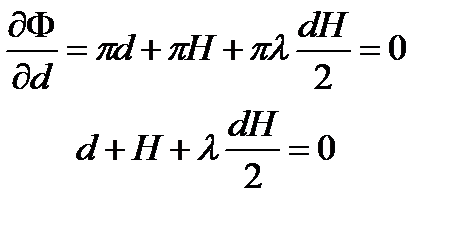
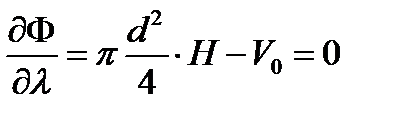
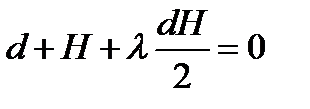

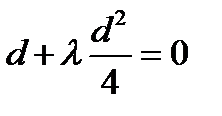
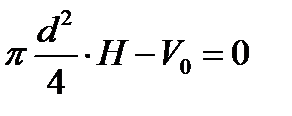
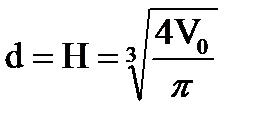 получим, что для минимальной поверхности цилиндра должно выполняться соотношение:
получим, что для минимальной поверхности цилиндра должно выполняться соотношение: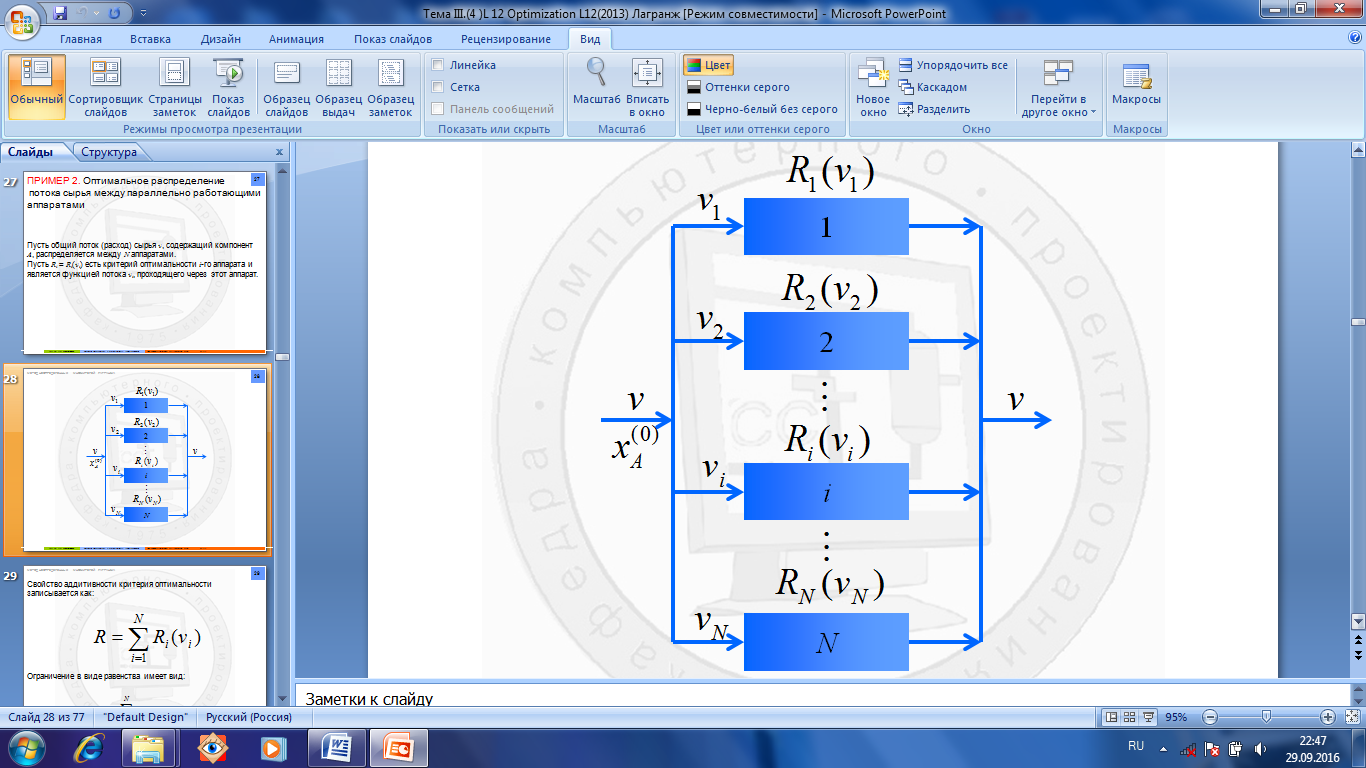
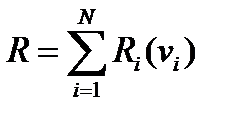 Рис.1.6.1. Распределение между параллельными аппаратами
Рис.1.6.1. Распределение между параллельными аппаратами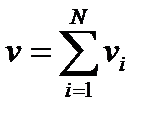 Свойство аддитивности критерия
Свойство аддитивности критерия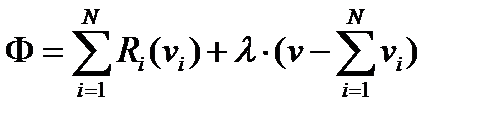 Функция Лагранжа:
Функция Лагранжа: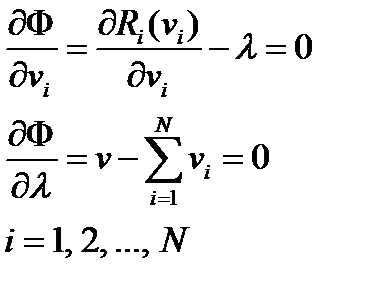 Дифференцируя и приравнивая нулю
Дифференцируя и приравнивая нулю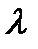 уравнений для определения vi (i=1,…n)
уравнений для определения vi (i=1,…n)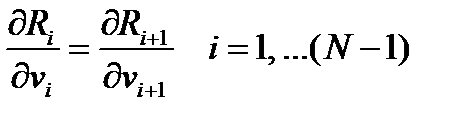 Отсюда следует, что при оптимальных условиях распределения потока в параллельно работающих аппаратах
Отсюда следует, что при оптимальных условиях распределения потока в параллельно работающих аппаратах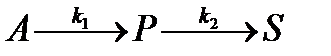 Рассчитать оптимальное распределение (рис.1.6.2) потока сырья v, поступающего на параллельно работающие реакторы идеального смешения, в которых проводится реакция типа
Рассчитать оптимальное распределение (рис.1.6.2) потока сырья v, поступающего на параллельно работающие реакторы идеального смешения, в которых проводится реакция типа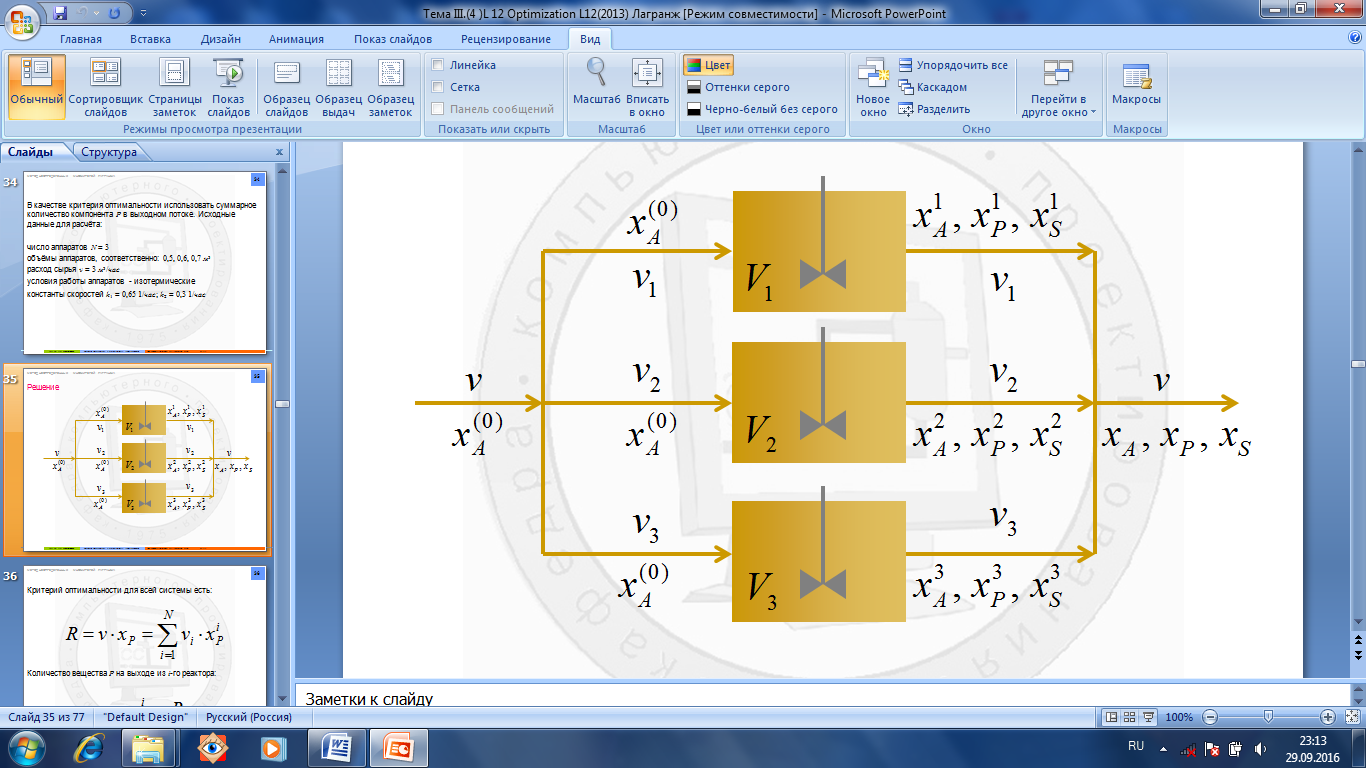
 Критерий оптимальности
Критерий оптимальности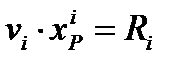 для всей системы есть:
для всей системы есть: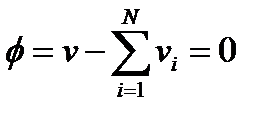 Количество вещества P на выходе из i -го реактора:
Количество вещества P на выходе из i -го реактора: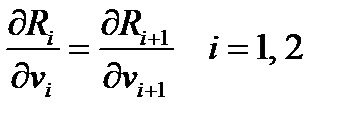
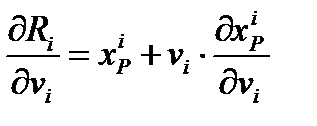
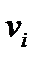
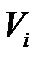
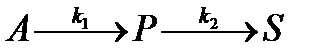 Уравнения материального баланса по компонентам A и P для i -го реактора с расходом потока в нем и его объемом для реакции
Уравнения материального баланса по компонентам A и P для i -го реактора с расходом потока в нем и его объемом для реакции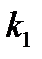
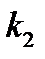
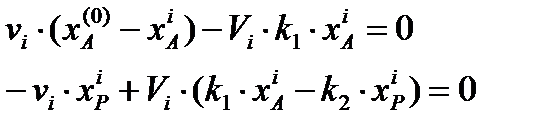 где , - константы скоростей реакции:
где , - константы скоростей реакции: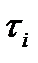 Уравнения материального баланса по компонентам A и P для i -го реактора с использованием времени пребывания в реакторе имеют вид:
Уравнения материального баланса по компонентам A и P для i -го реактора с использованием времени пребывания в реакторе имеют вид: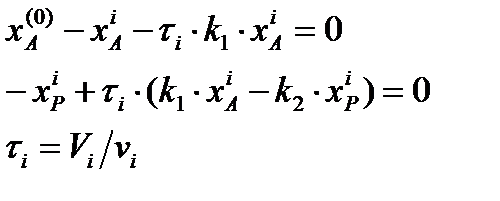
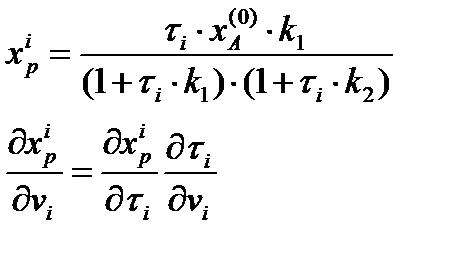 Из полученной системы уравнений выразим концентрацию компонента P в i – том аппарате через начальную концентрацию компонента A:
Из полученной системы уравнений выразим концентрацию компонента P в i – том аппарате через начальную концентрацию компонента A: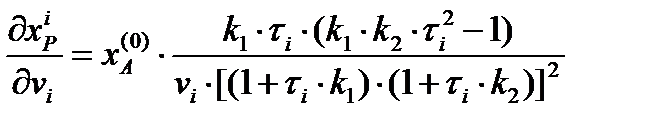
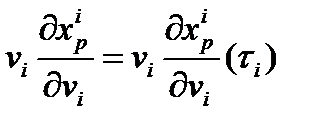
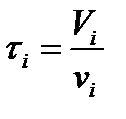 Из полученного выражения
Из полученного выражения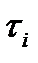 следует, что произведение
следует, что произведение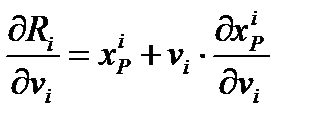
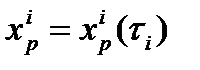
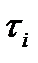 зависит от времени пребывания,а также из уравнений материальных балансов следует тоже зависимость только от времени пребывания :
зависит от времени пребывания,а также из уравнений материальных балансов следует тоже зависимость только от времени пребывания :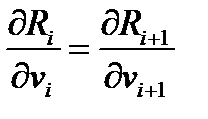
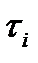 Так как в выражении для рассматриваемой реакции:
Так как в выражении для рассматриваемой реакции: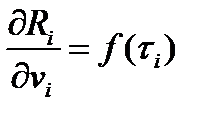 оба слагаемых зависят от а также поскольку:
оба слагаемых зависят от а также поскольку: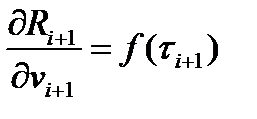
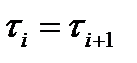
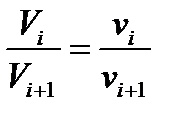
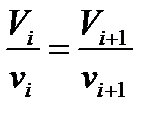 и имеем:
и имеем: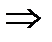 Откуда следует:
Откуда следует: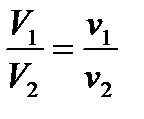
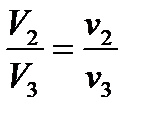
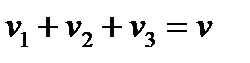
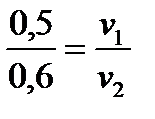
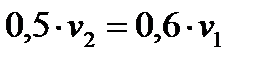
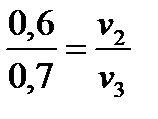 Подставляя исходные данные, получим:
Подставляя исходные данные, получим: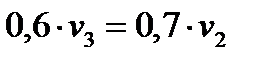
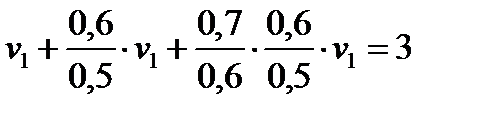 Подставляя исходные данные, получим:
Подставляя исходные данные, получим: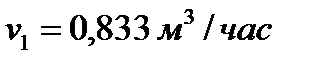
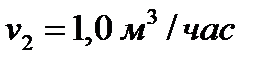
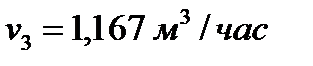 Откуда находим:
Откуда находим: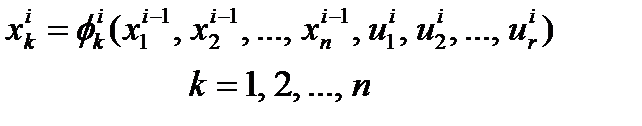 Рассмотрим многостадийный процесс (рис.1.6.3), состоящий из стадий, каждая из которых описывается системой
Рассмотрим многостадийный процесс (рис.1.6.3), состоящий из стадий, каждая из которых описывается системой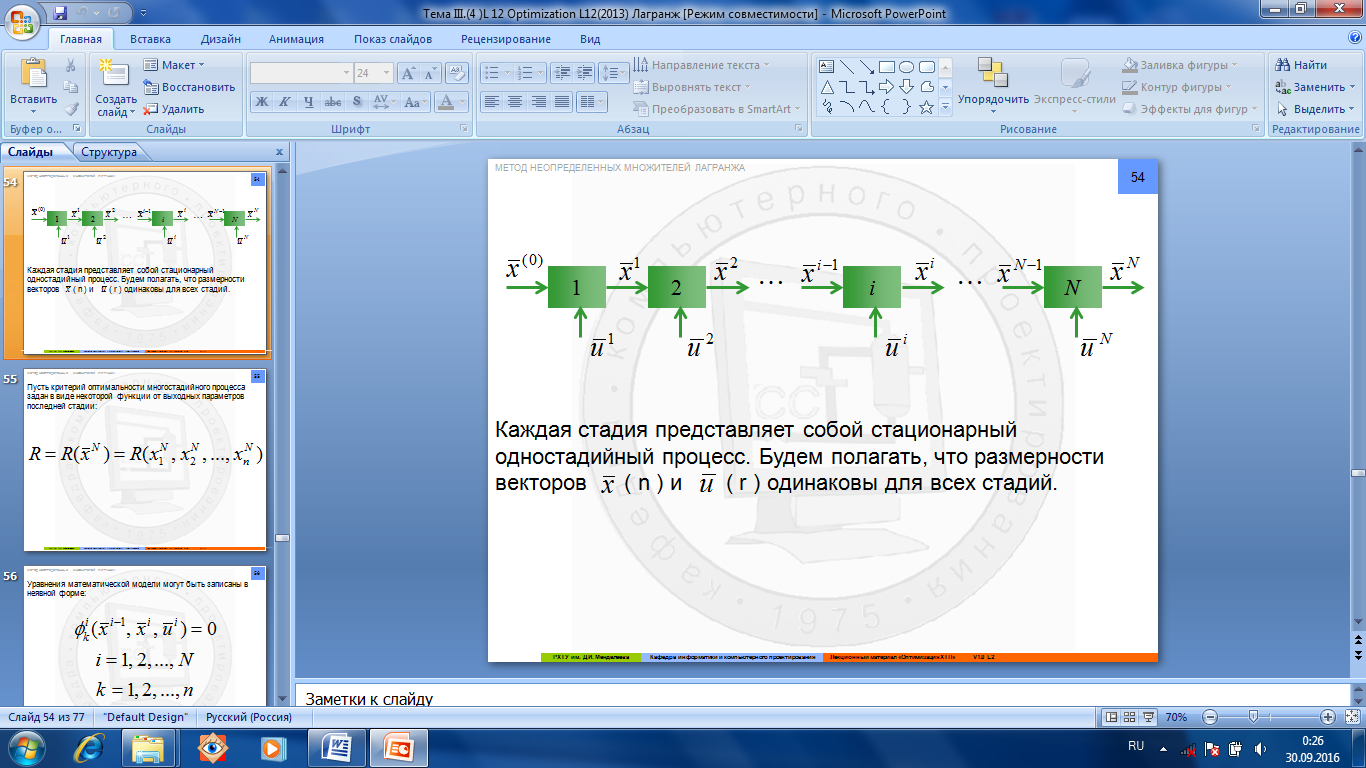
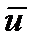
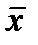 Каждая стадия представляет собой стационарный одностадийный процесс. Будем полагать, что размерности векторов (n) и (r) одинаковы для всех стадий.
Каждая стадия представляет собой стационарный одностадийный процесс. Будем полагать, что размерности векторов (n) и (r) одинаковы для всех стадий.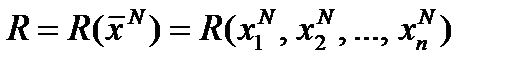 Пусть критерий оптимальности многостадийного процесса задан в виде некоторой функции от выходных
Пусть критерий оптимальности многостадийного процесса задан в виде некоторой функции от выходных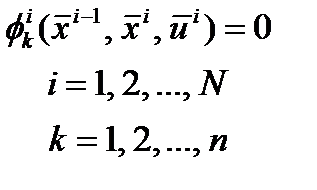 параметров последней стадии:
параметров последней стадии: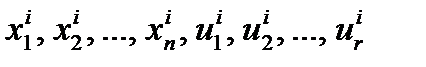 При использовании метода неопределённых множителей Лагранжа для решения задачи оптимизации соотношения математической модели на всех стадиях используются как ограничения, наложенные на переменные, часть из которых входит в
При использовании метода неопределённых множителей Лагранжа для решения задачи оптимизации соотношения математической модели на всех стадиях используются как ограничения, наложенные на переменные, часть из которых входит в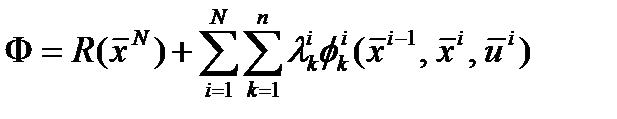 выражение для критерия оптимальности:
выражение для критерия оптимальности: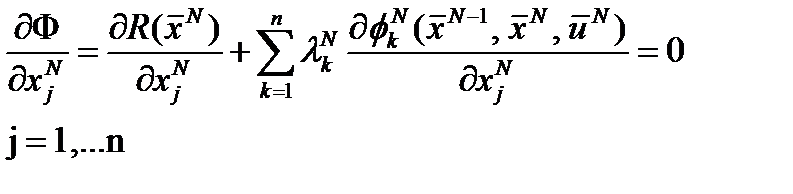
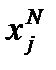 При дифференцировании функции Лагранжа по всем переменным получим три типа уравнений:
При дифференцировании функции Лагранжа по всем переменным получим три типа уравнений: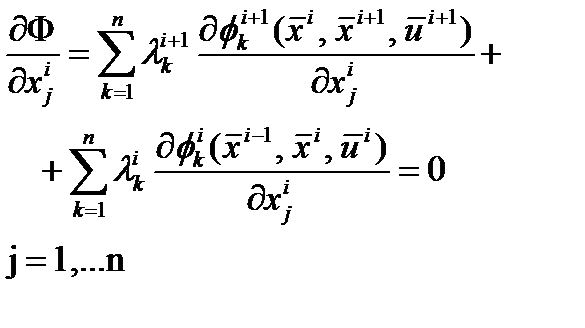 дифференцирование по:
дифференцирование по: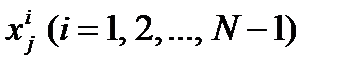 дифференцирование
дифференцирование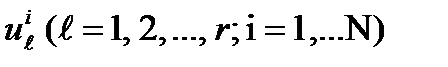
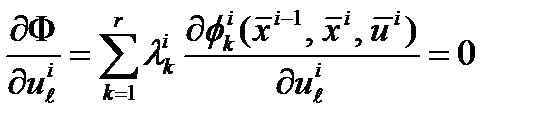 дифференцирование по
дифференцирование по 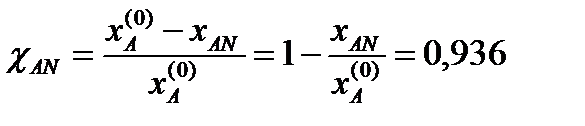 Решение
Решение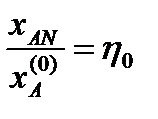 условиям ограничения:
условиям ограничения: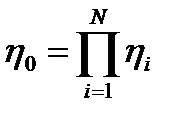
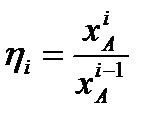 Тогда для каждого реактора каскада и для всех аппаратов:
Тогда для каждого реактора каскада и для всех аппаратов: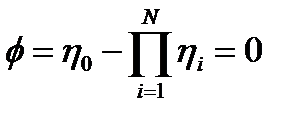
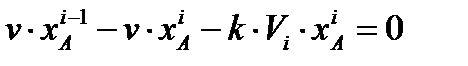 Выразим критерий оптимальности через
Выразим критерий оптимальности через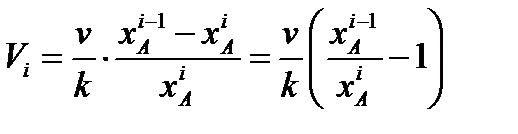 η i, используя уравнения материального
η i, используя уравнения материального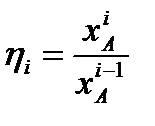 Выразим объём i -го реактора как:
Выразим объём i -го реактора как: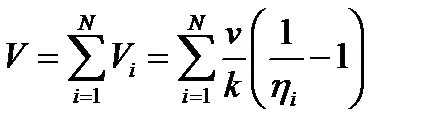
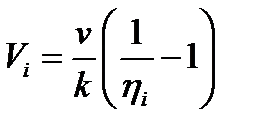 Учитывая, что
Учитывая, что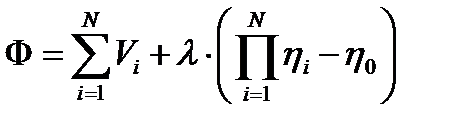 Будем искать такое распределение η i, чтобы V = min
Будем искать такое распределение η i, чтобы V = min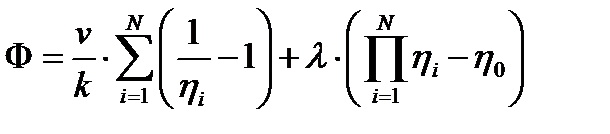 или
или
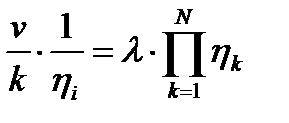 Необходимые условия оптимальности:
Необходимые условия оптимальности: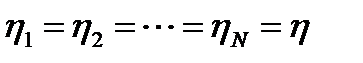
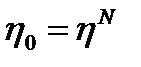 Поскольку последнее соотношение справедливо для любого номера i, имеем:
Поскольку последнее соотношение справедливо для любого номера i, имеем: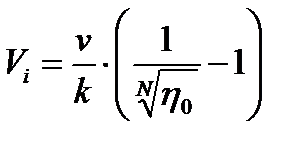 т.е. распределение η i по всем аппаратам каскада должно быть одинаковым. Из последнего соотношения также следует, что распределение объёмов реакторов должно быть
т.е. распределение η i по всем аппаратам каскада должно быть одинаковым. Из последнего соотношения также следует, что распределение объёмов реакторов должно быть