
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод наискорейшего спуска (крутого восхождения)Содержание книги
Поиск на нашем сайте
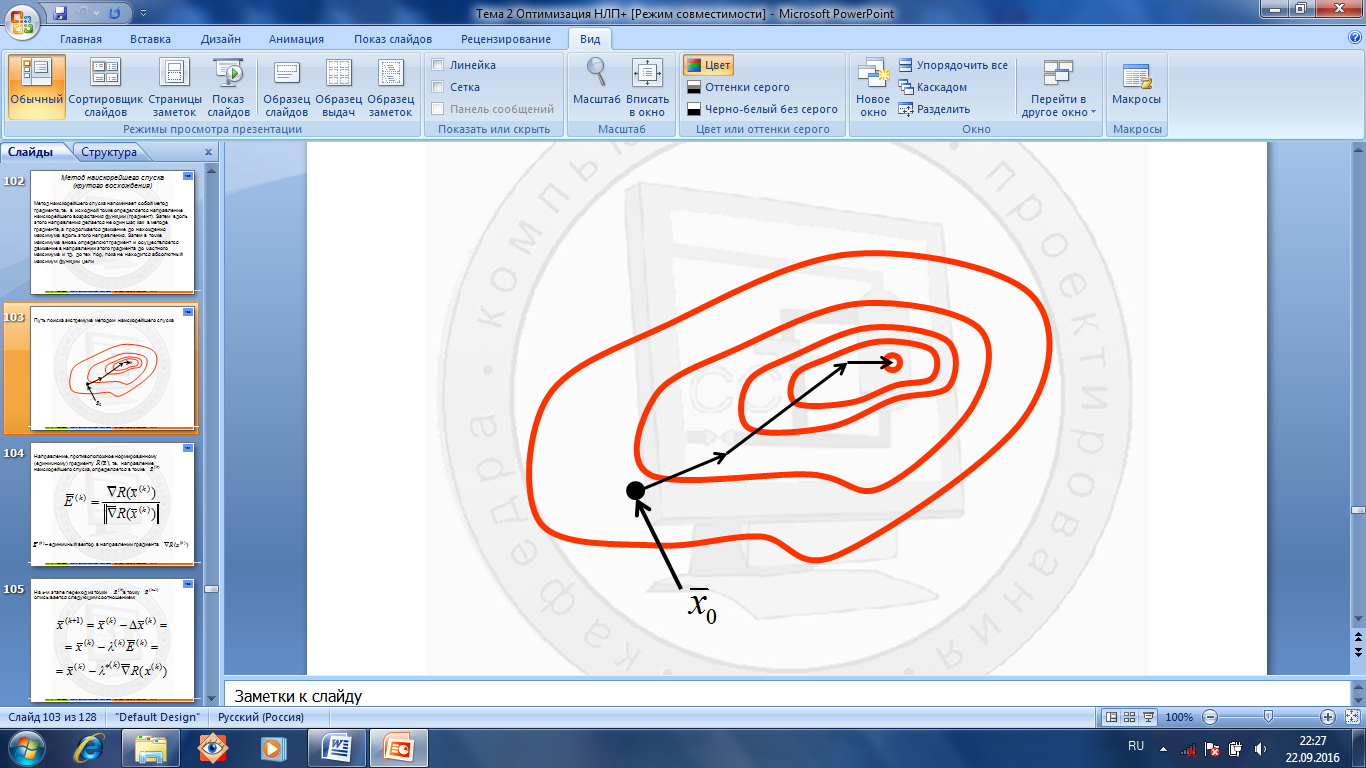
Метод наискорейшего спуска напоминает собой метод градиента, т.е. в исходной точке определяется направление наискорейшего возрастания функции (градиент). Затем вдоль этого направления делается не один шаг, как в методе градиента, а продолжается движение до нахождения максимума вдоль этого направления. Затем в точке максимума вновь определяют градиент и осуществляется движение в направлении этого градиента до частного максимума и т.д. до тех пор, пока не находится абсолютный максимум функции цели
Рис.1.4.17. Метод наискорейшего спуска.
, т.е. направление наискорейшего спуска, определяется в точке
описывается следующим соотношением:
Подстановка в последнее выражение
Тогда Поиск в соответствии с этим выражением осуществляется многократно.
Это может осуществляться формально путем вычисления λ из уравнения: Но чаще используют тот или иной метод одномерного поиска для определения величины λ *(k), минимизирующей на k -м шаге поиска целевую функцию. Метод наискорейшего спуска позволяет найти экстремум при минимальном объеме вычислений. Метод особенно выгодно использовать в том случае, когда градиент функции изменяется не резко. Очевидно, что вблизи экстремума метод наискорейшего спуска вырождается в метод градиента. В качестве критерия окончания поиска можно использовать те же критерии, что и в методе градиента.
Метод релаксаций Метод также использует производные, в частности, – первые производные целевой функции и состоит в нахождении осевого направления, вдоль которого целевая функция возрастает наиболее быстро.
Алгоритм поиска при методе релаксаций
hj– фактор шага, величина которого изменяется в процессе поиска
Обычно шаг выбирается так: вначале он принимается равным числу h1 = δ, затем делается еще один шаг в этом направлении h2 = h1, если шаг оказался успешным, то он удваивается h3 = 2h2. Если же следующий шаг оказался не успешным, то из предыдущей точки, в которой был удачный шаг, делаются шаги в 2 раза меньше, чем последний удачный. Уменьшение величины шага в области максимума производится до заданного значения, определяемого желаемой точностью. Метод релаксаций можно рассматривать как комбинацию методов, использующих производные.
|
|||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.73.202 (0.006 с.) |

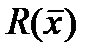
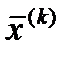 Направление, противоположное нормированному (единичному) градиенту
Направление, противоположное нормированному (единичному) градиенту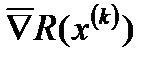
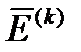 – единичный вектор в направлении градиента
– единичный вектор в направлении градиента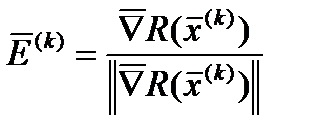
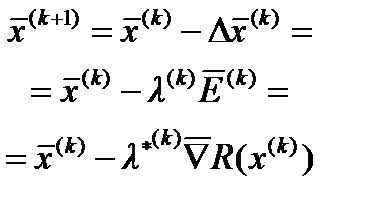
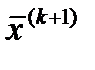 На k -м этапе переход из точки в точку
На k -м этапе переход из точки в точку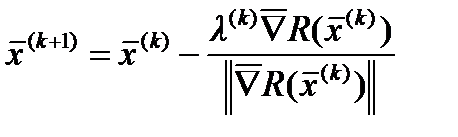 предыдущего дает следующее
предыдущего дает следующее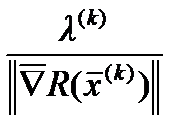 соотношение для метода наискорейшего спуска:
соотношение для метода наискорейшего спуска: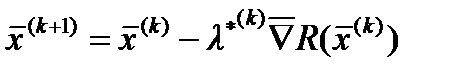 Поскольку выражение – скалярная величина, то оно может быть заменено некоторым числом λ*(k)
Поскольку выражение – скалярная величина, то оно может быть заменено некоторым числом λ*(k)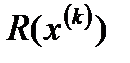 Для каждого направления градиента осуществляется минимизация
Для каждого направления градиента осуществляется минимизация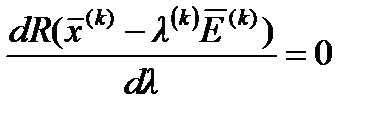 функции
функции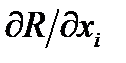 Для этого в начальной точке поиска определяются производные функции по всем переменным
Для этого в начальной точке поиска определяются производные функции по всем переменным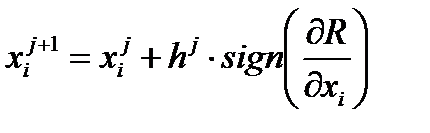 По той оси, вдоль которой производная наибольшая, и производится движение до частного минимума одномерным методом поиска. Затем анализ производных вновь повторяется. Критерием окончания поиска может служить следующее положение: если при движении из очередной точки не наблюдается дальнейшее возрастание целевой функции, то максимум найден.
По той оси, вдоль которой производная наибольшая, и производится движение до частного минимума одномерным методом поиска. Затем анализ производных вновь повторяется. Критерием окончания поиска может служить следующее положение: если при движении из очередной точки не наблюдается дальнейшее возрастание целевой функции, то максимум найден.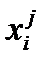 имеет вид:
имеет вид: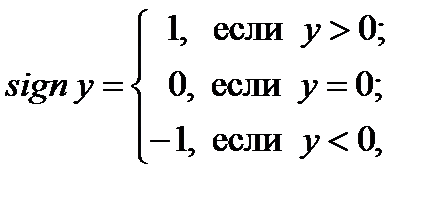 – значение переменной, по которой происходит оптимизация на данном шаге
– значение переменной, по которой происходит оптимизация на данном шаге


