
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод динамического программированияСодержание книги
Поиск на нашем сайте
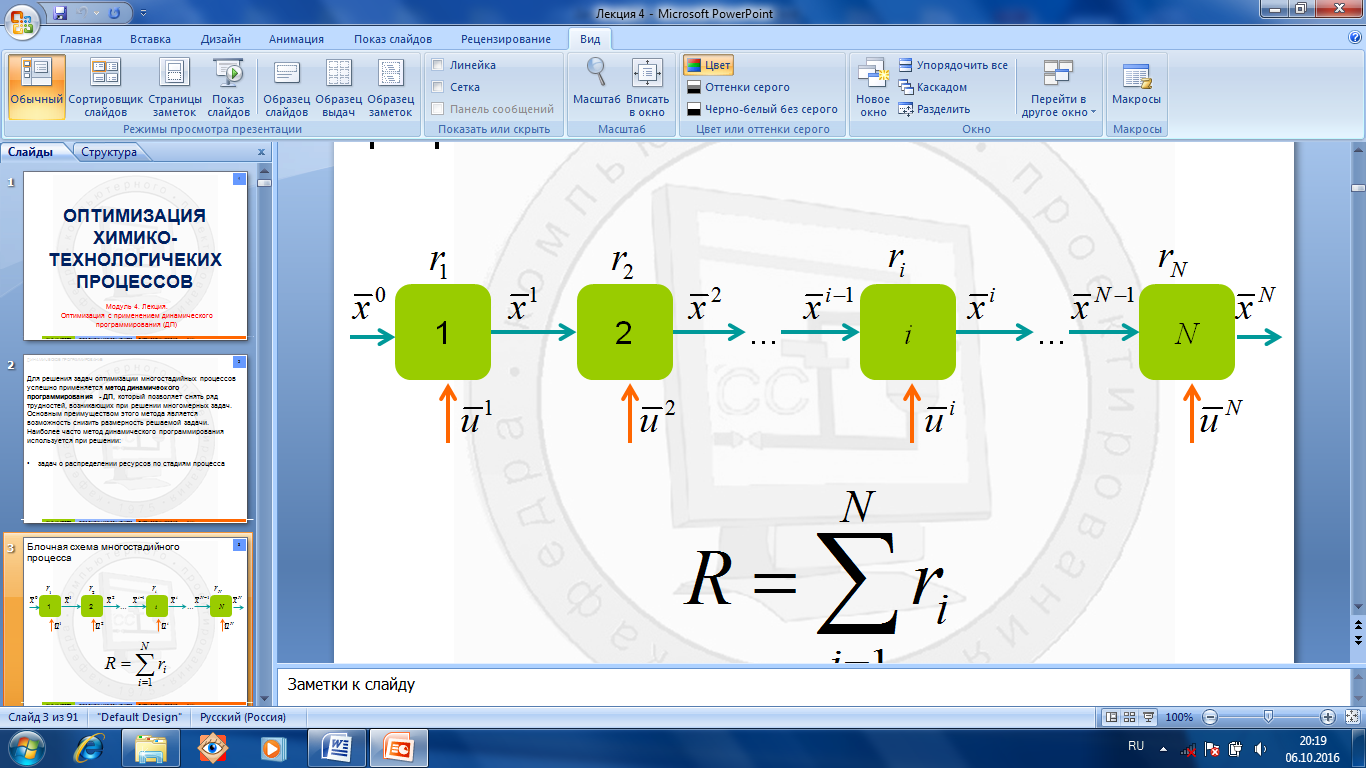
Для решения задач оптимизации многостадийных процессов успешно применяется метод динамического программирования - ДП, который позволяет снять ряд трудностей, возникающих при решении многомерных задач.Основным преимуществом этого метода является возможность снизить размерность решаемой задачи. Наиболее часто метод динамического программирования используется при решениизадач о распределении ресурсов по стадиям процесса. Блочная схема (рис.1.7.1) многостадийного процесса
Рис.1.7.1. Многостадийный процесс Условные обозначения на схеме каскада аппаратов: число стадий процесса (аппаратов) N
Критерий оптимальности всего процесса – аддитивная функция
стадии определяется её состоянием:
параметров и вектором управлений:
Рассмотрим задачу: Сырьё определённого состава поступает в каскад из трёх изотермических реакторов. По техническому регламенту для каждого реактора допускается реализация трёх стационарных состояний, определяемых набором параметров: n – число оборотов мешалки tн – температура хладагента G – расход хладагента
Рис.1.7.2. Входные и выходные составы
n – число оборотов мешалки tн – температура хладагента G – расход хладагента
Тогда задача оптимизации формулируется следующим образом: Задача оптимизации ставится следующим образом: найти такой набор управлений на каждом из реакторов, чтобы критерий оптимальности всего процесса R достиг максимального значения.
Схематическое изображение (рис.1.7.3) процесса в рассматриваемом трехстадийном процессе:
Рис.1.7.3. Изображение схемы многостадийного процесса
k – соответствует числу состояний (k =3),
Далее предположим, что реализация любого управления на любом реакторе связана с некоторым значением критерия оптимальности в этом реакторе. На схеме цифрами проставлены условные значения критерия оптимальности на каждой стадии в зависимости от применяемого набора
в i -ом реакторе Проще всего эта задача может быть решена обычным перебором (1-й способ решения), т.е. сравнением между собой всех возможных вариантов проведения процесса. Необходимо определить значение R для всех ломаных (здесь 27) схемы процесса:
Из всех полученных значений R выбирается максимальный и, следовательно, выбирается реализующий его набор управлений. Однако этот путь решения имеет существенный недостаток - требуется производить анализ всех возможных вариантов, число которых быстро возрастает с ростом числа стадий и числа допустимых состояний. Изложенный метод решения задачи требует реализации большого количества необходимых вычислений. Формула для количества возможных вариантов вычислений при использовании метода перебора (1-ый способ решения) имеет вид:
N – число стадий В соответствии с принципом оптимальности, которым необходимо руководствоваться при решении таких задач, и который лежит в основе динамического программирования (2-ой способ решения): для любого промежуточного состояния процесса последующие управления должны быть оптимальными. В соответствии с этим принципом решение задачи методом ДП включает 2 этапа: 1 этап: начинается с выбора оптимального управления на последней стадии, затем на предпоследней и т.д., двигаясь от конца процесса к его началу. Однако значения этих управлений зависят от входных параметров на каждую стадию, включая первую стадию. Входные параметры на первую стадию либо известны, либо определяются по результатам расчетов первой стадии. 2 этап: по известным значениям входных параметров, начиная с первой стадии определяются конкретные управляющие параметры последовательно на всех стадиях процесса до последней стадии, что и является решением задачи.
При k = 3 и N = 3 n’ = 21, в то время как в 1-ом способе - n = 27 При k = 3 и N = 5 n’ = 39, в то время, как в 1-м - n = 243.
|
|||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 110; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.157.241 (0.005 с.) |

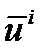
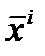 вектор переменных состояния процесса на выходе из i -того аппарата и на входе в i +1 аппарат
вектор переменных состояния процесса на выходе из i -того аппарата и на входе в i +1 аппарат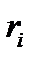 вектор переменных управления i -том аппарате
вектор переменных управления i -том аппарате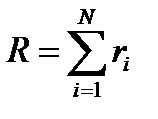 частный критерий оптимальности в i -том аппарате
частный критерий оптимальности в i -том аппарате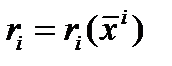 Критерий оптимальности на каждой
Критерий оптимальности на каждой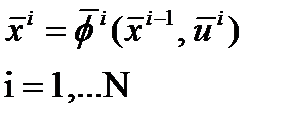 Уравнение математической модели для i –й стадии даёт связь между вектором входных параметров, вектором выходных
Уравнение математической модели для i –й стадии даёт связь между вектором входных параметров, вектором выходных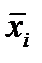 Каждому стационарному состоянию соответствует (рис.1.7.2) некоторый состав на выходе из аппарата.
Каждому стационарному состоянию соответствует (рис.1.7.2) некоторый состав на выходе из аппарата.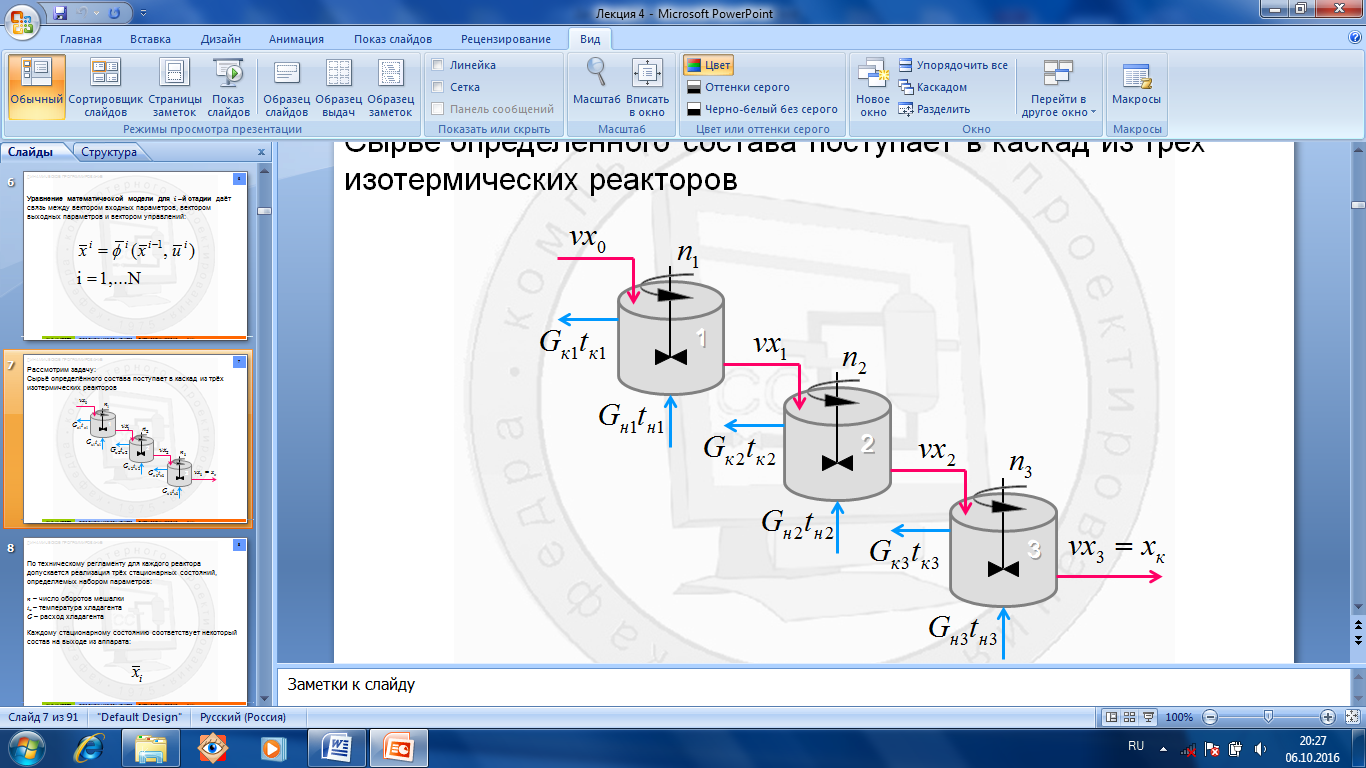
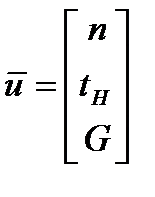 Вектор искомых управляющих переменных на каждой стадии имеет вид:
Вектор искомых управляющих переменных на каждой стадии имеет вид: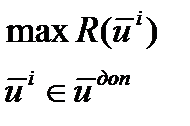
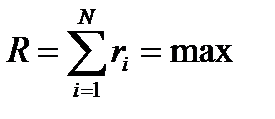 В соответствии со схемой, решение задачи оптимизации методом перебора всех вариантов управлений, т.е.комбинаторным методом это означает такой выбор одной или нескольких ломаных линий из всей их совокупности, чтобы выполнилось следующее равенство:
В соответствии со схемой, решение задачи оптимизации методом перебора всех вариантов управлений, т.е.комбинаторным методом это означает такой выбор одной или нескольких ломаных линий из всей их совокупности, чтобы выполнилось следующее равенство: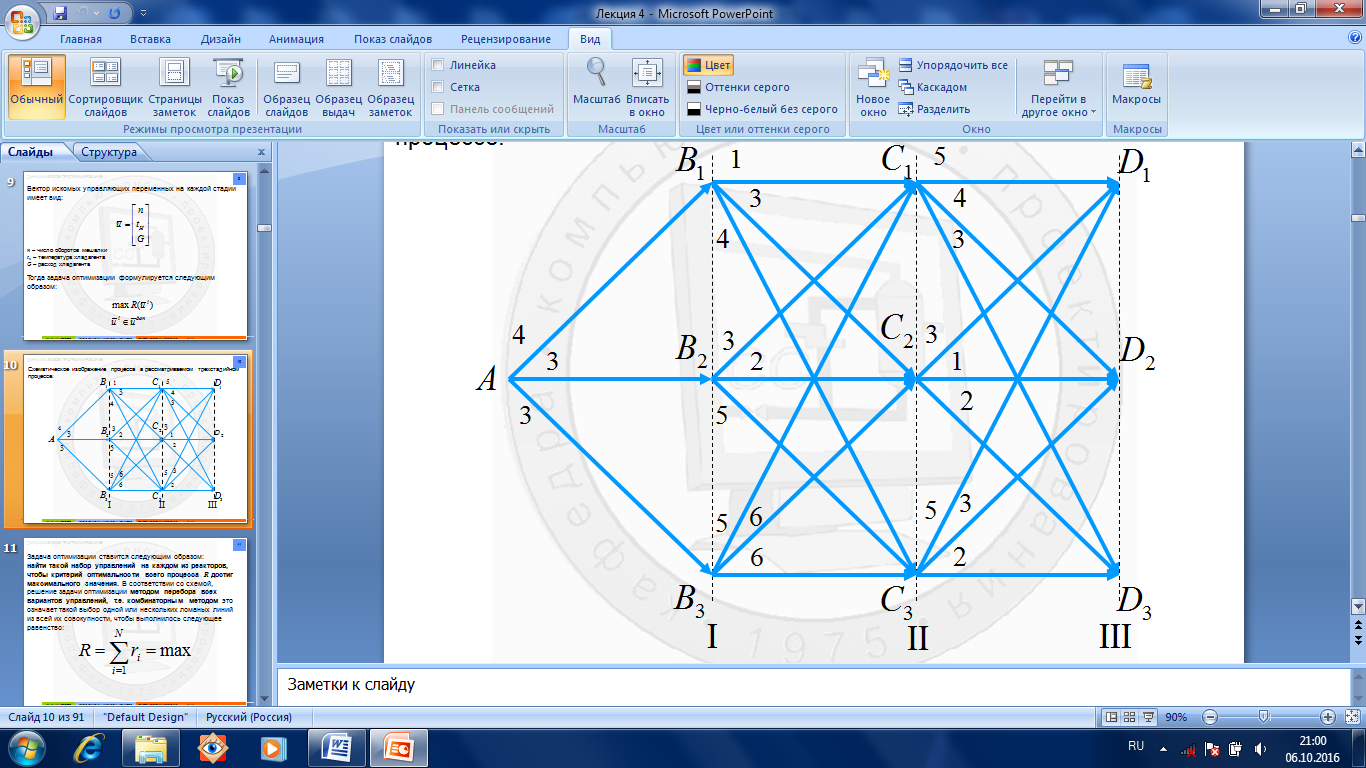
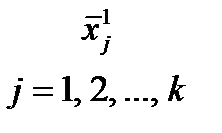 Точка A изображает начальное состояние процесса, которое характеризуется начальным составом сырья, его температурой и т.д. В результате определённого набора управлений на первом реакторе (n 1, tн 1, G 1) на выходе из него получается продукт с составом:
Точка A изображает начальное состояние процесса, которое характеризуется начальным составом сырья, его температурой и т.д. В результате определённого набора управлений на первом реакторе (n 1, tн 1, G 1) на выходе из него получается продукт с составом: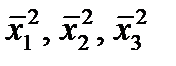 реализуемых в каждом случае. Далее переработка сырья во втором реакторе осуществляется таким образом, что на выходе из него получается следующий состав продуктов: . Эти состояния изображаются точками C 1, C 2 и C 3. Линии, соединяющие точки Bi и Cj, соответствуют тем наборам управлений на втором реакторе, которые используются при переводе системы из состояния Bi в состояние Cj.
реализуемых в каждом случае. Далее переработка сырья во втором реакторе осуществляется таким образом, что на выходе из него получается следующий состав продуктов: . Эти состояния изображаются точками C 1, C 2 и C 3. Линии, соединяющие точки Bi и Cj, соответствуют тем наборам управлений на втором реакторе, которые используются при переводе системы из состояния Bi в состояние Cj.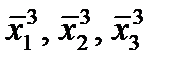 Аналогично для третьего реактора точки D 1, D 2 и D 3 соответствуют трём возможным стационарным состояниям на третьем реакторе, т.е. составам: . Линии, соединяющие точки C i и D j, соответствуют тем наборам управлений на третьем реакторе, которые используются при переводе системы из состояния C i в состояние D j.
Аналогично для третьего реактора точки D 1, D 2 и D 3 соответствуют трём возможным стационарным состояниям на третьем реакторе, т.е. составам: . Линии, соединяющие точки C i и D j, соответствуют тем наборам управлений на третьем реакторе, которые используются при переводе системы из состояния C i в состояние D j.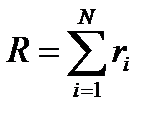 управлений. При этом будем считать, что критерий оптимальности всего процесса может быть выражен в виде:
управлений. При этом будем считать, что критерий оптимальности всего процесса может быть выражен в виде: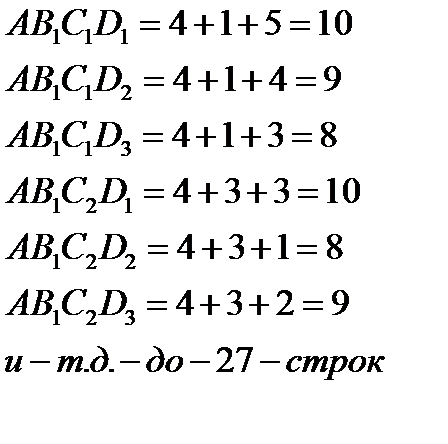 ri – значение критерия оптимальности
ri – значение критерия оптимальности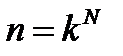 k – число возможных состояний на стадии
k – число возможных состояний на стадии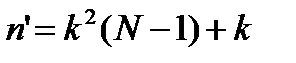 Если же задача решается изложенным методом динамического программирования (2-ой способ решения), необходимое количество вычислений (n’) составляет:
Если же задача решается изложенным методом динамического программирования (2-ой способ решения), необходимое количество вычислений (n’) составляет:


