
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численные методы оптимизации при наличии ограниченийСодержание книги
Поиск на нашем сайте
Все методы оптимизации при наличии ограничений делятся на два класса: методы сведения к задаче безусловного экстремума без ограничений и методы прямого решения задач с ограничениями. Среди методов, сводящих задачу с ограничениями к безусловной оптимизации, наиболее широко распространены методы штрафных функций.
Методы штрафных функций При решении задач оптимизации химико-технологической системы существует, как правило, ряд ограничений типа равенств (например, значения потоков в местах разрывов в схемах с обратной связью), так и ограничения типа неравенств (например, технологические ограничения по диапазону концентраций, температур, давления и т.д.).
при ограничениях
В основу методов штрафных функций положена идея преобразования общей нелинейной задачи в последовательность задач без ограничений путем добавления к целевой функции одной или нескольких функций, задающих ограничения с тем, чтобы ограничения, как таковые, в задаче оптимизации не фигурировали. Например, необходимо минимизировать функцию
Рис.1.4.18. Целевая функция Ясно, что ограничение x1 должно сдерживать любой шаговый метод поиска, такое ограничение называется активным.
целевая функция (штрафная функция):
Рис.1.4.19. Целевая штрафная функция и методом прохождения безусловного экстремума можно определить точку оптимума. Однако, получается точка, отстоящая от границы и, следовательно, от точного решения на величину (x1 – x*), что не всегда удовлетворяет точности решения задачи. Для того, чтобы удовлетворить точности, необходимо ввести некоторый множитель μ, который называется весовым коэффициентом (μ> 1).
Рис.1.4.20. Поиск оптимума, метод штрафных функций
μi – весовые коэффициенты
и 1, если Таким образом, вводя, штрафную функцию мы тем самым выделяем своеобразную «стену» на границе области и чем больше μi, тем она «круче». Однако на этой же границе образуется овраг, который резко замедляет скорость сходимости любого метода, а для некоторых он непроходим. Поэтому выбор весовых коэффициентов тоже является своеобразной задачей и от удачного выбора во многом зависит время решения задачи. Теория штрафных функций достаточно хорошо разработана и основана на идее изменения целевой функции таким образом, чтобы последовательность точек, получаемых в результате применения какого-либо метода безусловной оптимизации, одновременно сходилась и к выполнению всех ограничений и к минимальному значению целевой функции.
|
|||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 160; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.69.25 (0.007 с.) |

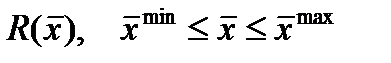 Тогда в общем виде задачу можно сформулировать следующим образом:
Тогда в общем виде задачу можно сформулировать следующим образом: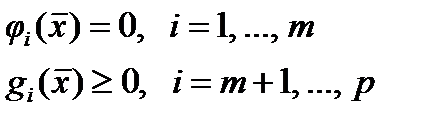 минимизировать
минимизировать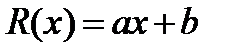
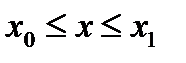 Где ОГРАНИЧЕНИЯ II-го РОДА имеют вид:
Где ОГРАНИЧЕНИЯ II-го РОДА имеют вид: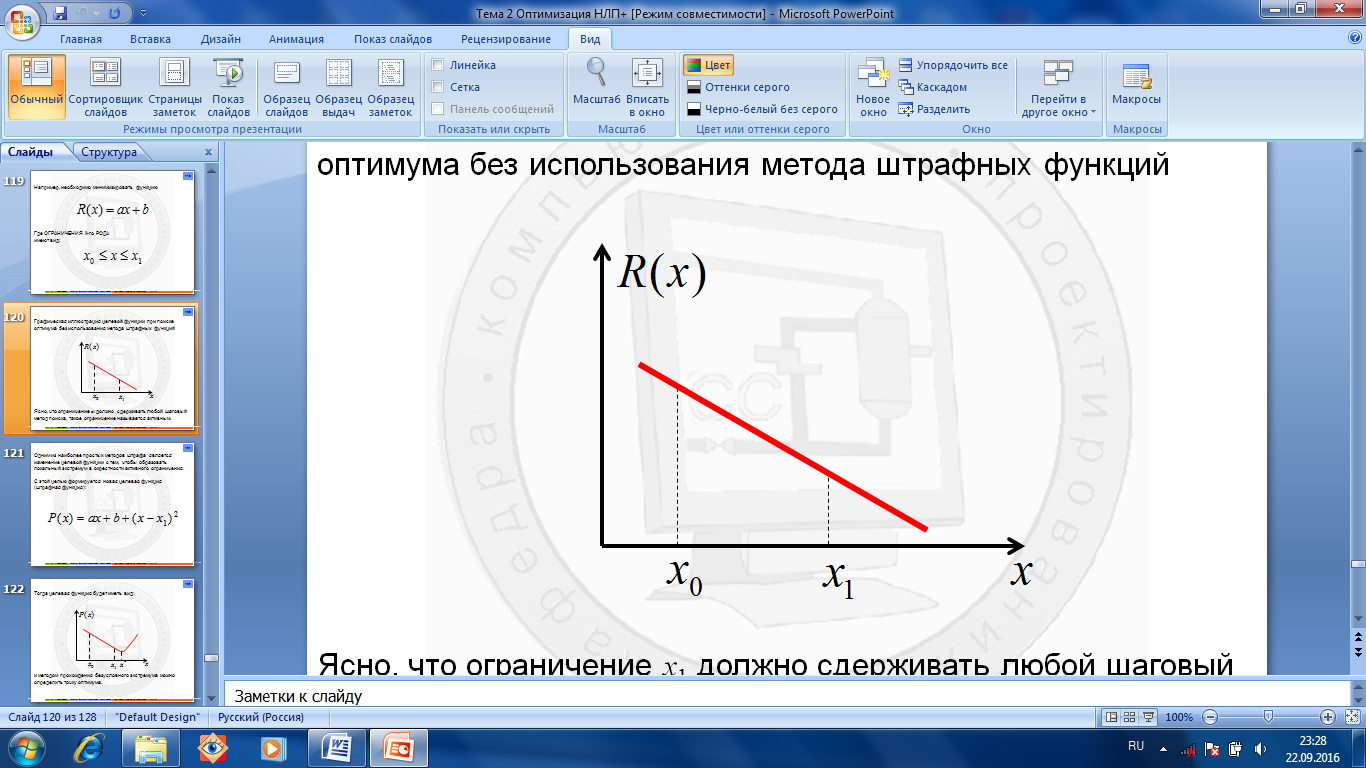
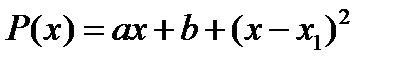 Одним из наиболее простых методов штрафа является изменение целевой функции с тем, чтобы образовать локальный экстремум в окрестности активного ограничения. С этой целью формируется новая
Одним из наиболее простых методов штрафа является изменение целевой функции с тем, чтобы образовать локальный экстремум в окрестности активного ограничения. С этой целью формируется новая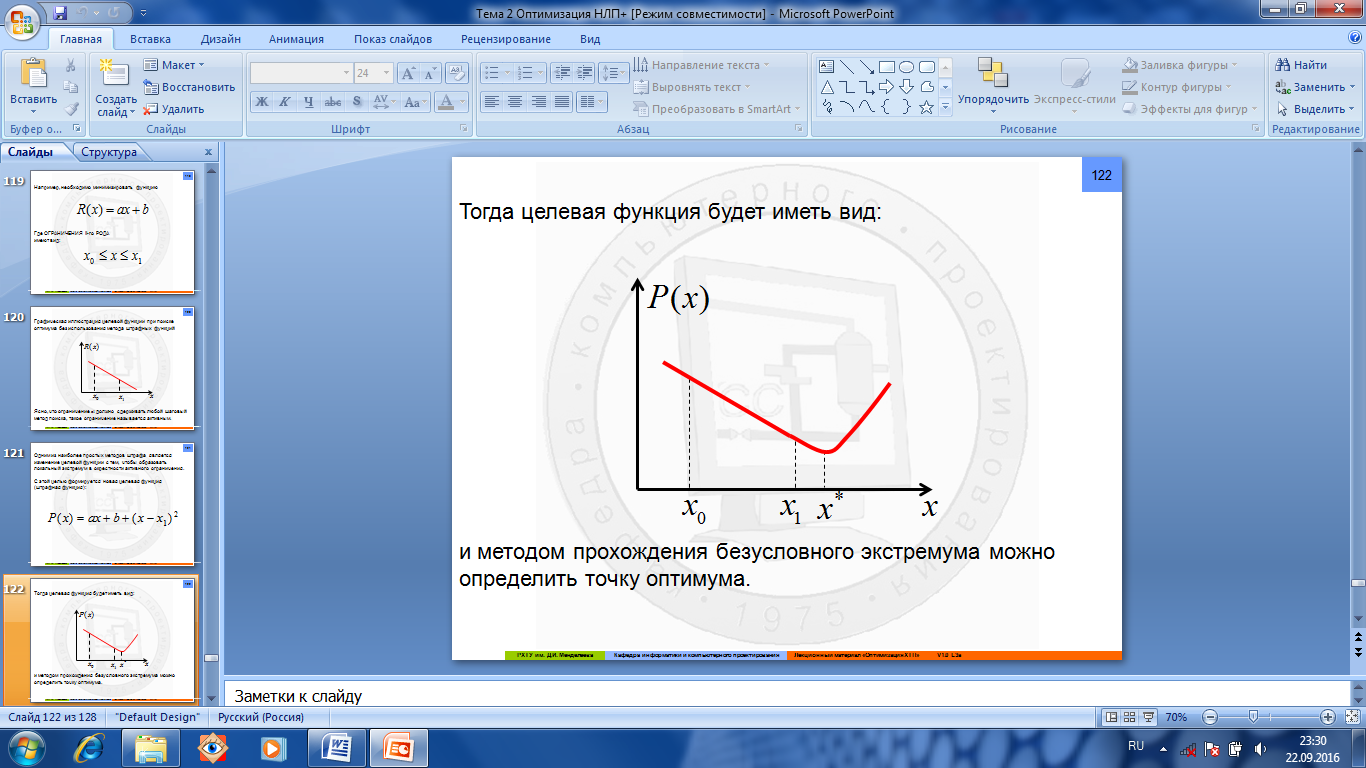
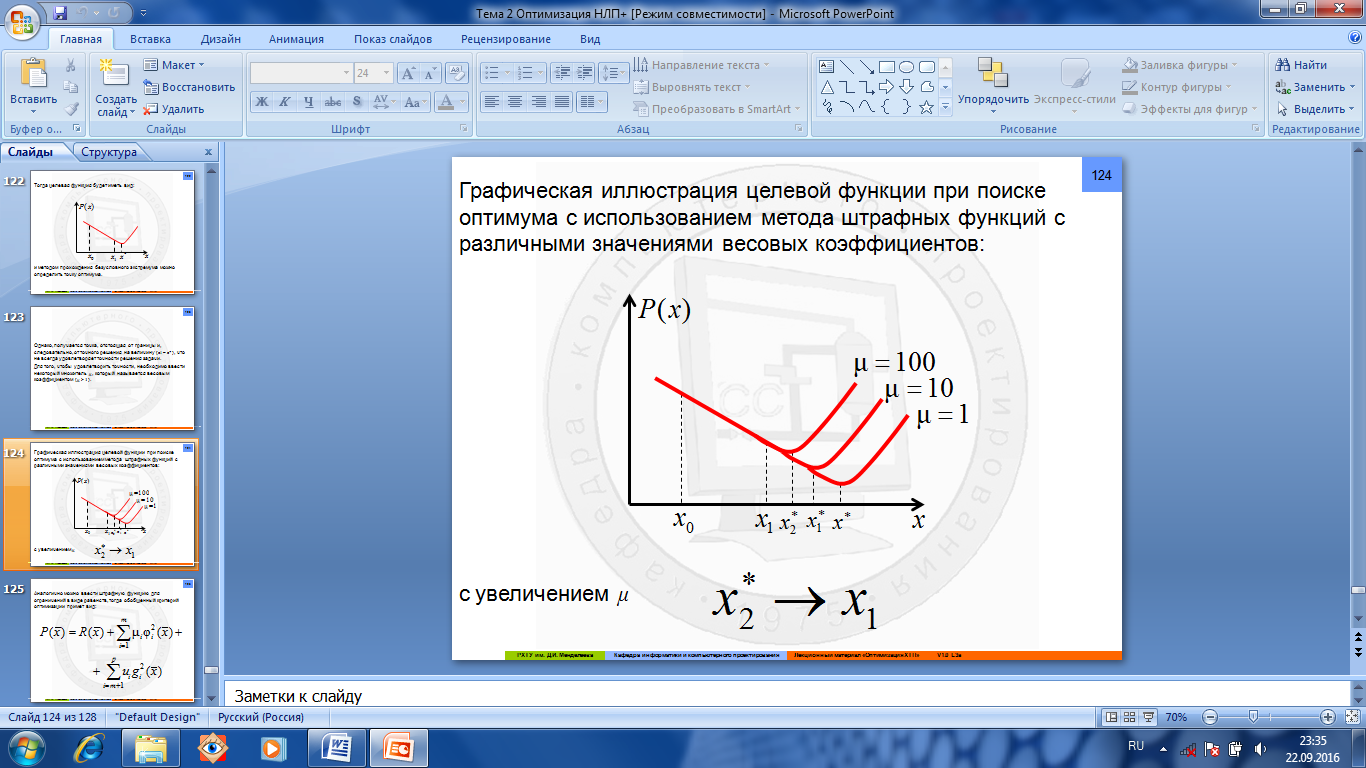
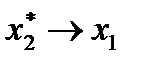 с увеличением μ
с увеличением μ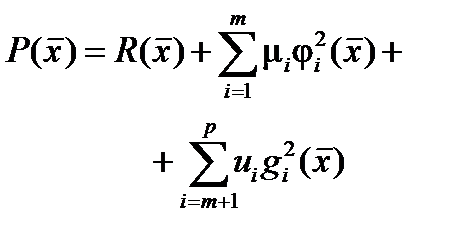 Аналогично можно ввести штрафную функцию для ограничений в виде равенств, тогда обобщенный критерий оптимизации примет вид:
Аналогично можно ввести штрафную функцию для ограничений в виде равенств, тогда обобщенный критерий оптимизации примет вид: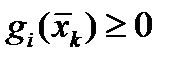
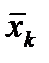 u – оператор Хевисайда,
u – оператор Хевисайда,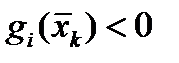 который принимает значения 0 и 1, если в точке
который принимает значения 0 и 1, если в точке


