
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимальная температура обратимой двухкомпонентной реакции в реакторе с мешалкойСодержание книги
Поиск на нашем сайте
Рассчитать оптимальную температуру проведения обратимой двухкомпонентной реакции в реакторе с мешалкой, используя в качестве критерия оптимальности выход целевого продукта P. Схема реакции:А Р. Порядок обеих стадий реакции первый. Константы равны: Решение. Материальный баланс по компонентам А и P для реактора идеального перемешивания: Из системы уравнений материального баланса определяется выражение для выхода компонента P: где
Необходимое условие существования экстремума:
Приравнивая числитель последнего выражения к нулю, получаем:
Получаем: Из последнего выражения следует:
Логарифмирование последнего выражения даёт:
Подставляя численные значения параметров, получаем:
Программа: Model 2_ T (построение графиков xa от T и xp от T. Графическое решение задачи. Поиск экстремума. Программа расчета оптимальной температуры (T - K) в изотермическом реакторе идеального смешения со стехиометрической схемой реакции A = P) Файл DATA. m Программный код файла DATA.m - задание исходной информации для расчетов; function DATA global xa0 A E R tau T_a T_b; Обнуляем вектор А и вектор Е A(2,1)=zeros; E(2,1)=zeros; Концентрация реагента А в долях в реакции A-P-S (мольные доли) xa0=1; Время пребывания в реакторе (мин) tau=10; Параметры уравнения Аррениуса для первой реакции a) Предэскпоненциальный множитель (мин^(-1)): A(1,1)=70; б) Энергия активации (кал/моль): E(1,1)=2500; Параметры уравнения Аррениуса для второй реакции a) Предэскпоненциальный множитель (мин^(-1)): A(2,1)=100; б) Энергия активации (кал/моль): E(2,1)=5000; Левая граница температурного интервала исследования (К); T_a=350; Правая граница температурного интервала исследования (К); T_b=370; Универсальная газовая постоянная (кал/моль/К): R=1.9872; end Файл model 2_ stat _ T. m Программный код файла model2_stat_T.m - расчет выходных концентраций продуктов из реактора. Значения вектора х функции model2_stat_T зависят от параметра «T». function x= model2_stat_T(T) global xa0 A E R tau; С помощью цикла «for» рассчитываем константы реакции k 1, k 2 for i=1:2 k(i)=A(i,1)*exp(-E(i,1)/R/T); end Обнуляем матрицу a и вектор b a=zeros(2,2);b=zeros(2,1); Для решения системы уравнений используем метод обратной матрицы. Преобразуем систему уравнений:
чтобы получить коэффициенты матрицы:
Задание коэффициентов матрицы А (коэффициенты перед вектора В (коэффициенты правой части системы уравнений, после знака «равно»). a(1,1)=1+k(1)*tau;a(1,2)=-k(2)*tau;b(1)=xa0; a(2,1)=tau*k(1);a(2,2)=(-1-tau*k(2)); b(2)=0; Определение выходных параметров модели. А=х*В. х=А/В. х=А-1*В x=inv(a)*b; Оператор inv (а) - поиск обратной матрицы А end Файл GLAV _ model 2_ grafik. m Программный код файла GLAV_model2_grafik.m - главная управляющая программа clc; clear all; close all; global TT xa xp T_a T_b; i=0; DATA; Задаем значение коэффициента T (температура, К) в интервале от T_a до T_b с шагом 1 for T=T_a:1:T_b i=i+1; Вызываем функцию x = model 2_ stat _ T (T) x= model2_stat_T(T); Массив значений коэффициента Т(К) в интервале от T _ a до T _ b с шагом 1 TT(i)=T; Массив значений коэффициента ха (мол.дол) - концентрации продукта А на выходе из реактора в заданном интервале температур от T _ a до T _ b xa(i)=x(1); Массив значений коэффициента хр (мол.дол) - концентрации продукта Р на выходе из реактора в заданном интервале температур от T _ a до T _ b xp(i)=x(2); end REPORT; Файл REPORT.m function REPORT; global xa0 A E tau TT xa xp T_a T_b R; Выводим на экран необходимый текст. disp('ПРОГРАММА РАСЧЕТА ОПТИМАЛЬНОЙ ТЕМПЕРАТУРЫ В ИЗОТЕРМИЧЕСКОМ РЕАКТОРЕ ИДЕАЛЬНОГО ПЕРЕМЕШИВАНИЯ '); РЕАКЦИЯ: A = P '); disp('Программа включает следующие файлы: GLAV_model2_grafik.m+DATA.m+model2_stat_T+REPORT.m'); disp('ИСХОДНЫЕ ДАННЫЕ '); Оператор num2str(xa0,'%10.2f') переводит числовые значения в строковые. Для этого необходимо записать оператор num2str, далее в скобках указываем переменную, которую необходимо перевести в строковый формат «xa0», затем ставим запятую «,» либо пробел и в одинарных кавычках через точку указываем число символов (%10)в строковой переменной и количество знаков после запятой(2f). disp(['1.Концентрация реагента A на входе в реактор (xa0) = ' num2str(xa0,'%10.2f') ' мольные доли']); disp(['2.Предэкспоненциальный множитель первой реакции(A(1)) = ' num2str(A(1),'%10.2f') ' мин^(-1)']); disp(['3.Энергия активация первой реакции(E(1)) = ' num2str(E(1),'%10.2f') ' кал/моль']); disp(['4.Предэкспоненциальный множитель второй реакции(A(2)) = ' num2str(A(2),'%10.2f') ' мин^(-1)']); disp(['5.Энергия активация второй реакции(E(1)) = ' num2str(E(2),'%10.2f') ' кал/моль']); disp(['6.Время пребывания в реакторе (tau) = ' num2str(tau,'%10.2f') ' мин']); disp(['7.Левая граница температурного интервала исследования (К)=' num2str(T_a,'%10.2f') ' K']); disp(['8.Правая граница температурного интервала исследования (К)=' num2str(T_b,'%10.2f') ' K']); disp(['9.Универсальная газовая постоянная (кал/моль/К)=' num2str(R,'%10.4f') ' кал/моль/К']); disp ('РЕЗУЛЬТАТЫ РАСЧЕТОВ'); disp ('1.Концентрации продуктов на выходе из реактора'); disp(' T(K) xa(мол.д.) xp(мол.д.) '); i=0; Выводим таблицу данных. Переменные T, xa, xp; for i=1:length(TT) TTT=TT(i);xaa=xa(i);xpp=xp(i); disp(sprintf('%10.3f\t %10.5f\t %10.5f',TTT,xaa,xpp)); end Построение графиков; hfig(1)=figure; hfig(2)=figure; Рисунок 1. График зависимости выхода продукта A от температуры в реакторе. figure(hfig(1)); Построение графика plot(TT,xa); Название графика title('График зависимости выхода продукта A от температуры в реакторе'); Подписи осей графика. xlabel('T - K');ylabel('Выходные концентрации: xa - мольные доли'); Наложение сетки на график grid on; Рисунок 2. График зависимости выхода продукта P от температуры в реакторе figure(hfig(2)); Построение графика plot(TT,xp); Название графика title('График зависимости выхода продукта P от температуры в реакторе'); Подписи осей графика. xlabel('T - K');ylabel('Выходные концентрации: xp - мольные доли'); Наложение сетки на график grid on; end
Optim2_T (Оптимальные значения режимных параметров реактора: температуры, концентрации продукта А на выходе из реактора, концентрации продукта Р на выходе из реактора. Программа расчета оптимальной температуры (T - K) в изотермическом реакторе идеального смешения со стехиометрической схемой реакции A = P) Файл DATA. m Программный код файла DATA.m - задание исходной информации для расчетов function DATA global xa0 A E R tau T_a T_b; Обнуляем вектор А и вектор Е A(2,1)=zeros;E(2,1)=zeros; Концентрация реагента А в долях в реакции A-P-S (мольные доли) xa0=1; Время пребывания в реакторе (мин) tau=10; Параметры уравнения Аррениуса для первой реакции a) Предэскпоненциальный множитель (мин^(-1)): A(1,1)=70; б) Энергия активации (кал/моль): E(1,1)=2500; Параметры уравнения Аррениуса для второй реакции a) Предэскпоненциальный множитель (мин^(-1)): A(2,1)=100; б) Энергия активации (кал/моль): E(2,1)=5000; Левая граница температурного интервала исследования (К); T_a=350; Правая граница температурного интервала исследования (К); T_b=370; Универсальная газовая постоянная (кал/моль/К): R=1.9872; end Файл model 2_ stat _ T. m Программный код файла model2_stat_T.m - расчет выходных концентраций продуктов из реактора и выход целевого продукта Р. Значения параметра phi _ p функции model2_stat_T зависят от параметра «T». function phi_p= model2_stat_T(T) global xa0 A E R tau xa xp; С помощью цикла «for» рассчитываем константы реакции k 1, k 2 for i=1:2 k(i)=A(i,1)*exp(-E(i,1)/R/T); end Обнуляем матрицу a и вектор b a=zeros(2,2);b=zeros(2,1); Для решения системы уравнений используем метод обратной матрицы. Преобразуем систему уравнений:
чтобы получить коэффициенты матрицы:
Задание коэффициентов матрицы А (коэффициенты перед вектора В (коэффициенты правой части системы уравнений, после знака «равно»). a(1,1)=1+k(1)*tau;a(1,2)=-k(2)*tau;b(1)=xa0; a(2,1)=tau*k(1);a(2,2)=(-1-tau*k(2)); b(2)=0; Определение выходных параметров модели. А=х*В. х=А/В. х=А-1*В Оператор inv (а) - поиск обратной матрицы А x=inv(a)*b; xa=x(1);xp=x(2); Вычисление критерия оптимальности phi _ p (целевой функции); В дальнейшем будет использоваться оператор «fminbnd», который находит минимум функции. Для того чтобы найти максимум функции с помощью оператора «fminbnd», мы ставим знак «-» перед x (2)/ xa 0 phi_p=-x(2)/xa0; end Файл GLAV _ maximum 2_ phi _ p. m Программный код файла GLAV_maximum2_phi_p.m - главная управляющая программа clc; clear all; close all; global T_opt phi_p_max T_a T_b; DATA; disp('Информация об итерационном процессе расчета'); Информация об итерационном процессе расчета iteration=optimset('Display','iter'); Реализация алгоритма поиска максимума функции одной переменной [T_opt,phi_p]=fminbnd('model2_stat_T',T_a,T_b,iteration); Знак «-» перед phi _ p необходим для корректного вывода данных экстремума функции. Оператор «fminbnd» находит минимум функции со знаком «-». Нам нужен максимум функции со знаком «+». phi_p_max=-phi_p; REPORT; Файл REPORT function REPORT Программныйкодфайла REPORT.m - отчетоработепрограммы global xa0 A E tau xa xp T_a T_b R T_opt phi_p_max; Выводим на экран необходимый текст. disp('ПРОГРАММА РАСЧЕТА ОПТИМАЛЬНОЙ ТЕМПЕРАТУРЫ В ИЗОТЕРМИЧЕСКОМ РЕАКТОРЕ ИДЕАЛЬНОГО ПЕРЕМЕШИВАНИЯ '); disp(' РЕАКЦИЯ: A = P '); disp('Программавключаетследующиефайлы: GLAV_model2_grafik.m+DATA.m+model2_stat_T+REPORT.m'); disp('ИСХОДНЫЕ ДАННЫЕ '); Оператор num2str(xa0,'%10.2f') переводит числовые значения в строковые. Для этого необходимо записать оператор num2str, далее в скобках указываем переменную, которую необходимо перевести в строковый формат «xa0», затем ставим запятую «,» либо пробел и в одинарных кавычках через точку указываем число символов (%10)в строковой переменной и количество знаков после запятой(2f). disp(['1.Концентрация реагента A на входе в реактор (xa0) = ' num2str(xa0,'%10.2f') ' мольные доли']); disp(['2.Предэкспоненциальный множитель первой реакции(A(1)) = ' num2str(A(1),'%10.2f') ' мин^(-1)']); disp(['3.Энергия активация первой реакции(E(1)) = ' num2str(E(1),'%10.2f') ' кал/моль']); disp(['4.Предэкспоненциальный множитель второй реакции(A(2)) = ' num2str(A(2),'%10.2f') ' мин^(-1)']); disp(['5.Энергия активация второй реакции(E(2)) = ' num2str(E(2),'%10.2f') ' кал/моль']); disp(['6.Время пребывания в реакторе (tau) = ' num2str(tau,'%10.2f') ' мин']); disp(['7.Левая граница температурного интервала исследования (К)=' num2str(T_a,'%10.2f') ' K']); disp(['8.Правая граница температурного интервала исследования (К)=' num2str(T_b,'%10.2f') ' K']); disp(['9.Универсальная газовая постоянная (кал/моль/К)=' num2str(R,'%10.4f') ' кал/моль/К']); disp ('РЕЗУЛЬТАТЫ РАСЧЕТОВ'); disp ('1.Оптимальные значения режимных параметров реактора'); disp(' T_opt(час) phi_p_maxxa(мол.д.) xp(мол.д.) '); Выводим таблицу данных. Переменные T _ opt, phi _ p _ max, xa, xp; disp(sprintf('%10.3f\t %10.5f\t %10.5f\t %10.5f',T_opt,phi_p_max,xa,xp)); end
|
||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 160; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.149.244 (0.008 с.) |

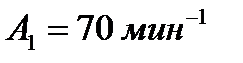 ;
; 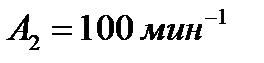 . Значения энергий активации стадий реакции:
. Значения энергий активации стадий реакции: 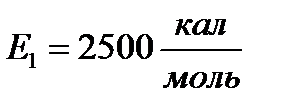 ;
; 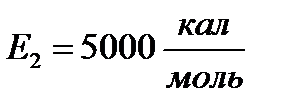 . Время пребывания в реакторе:
. Время пребывания в реакторе: 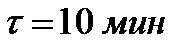 .
.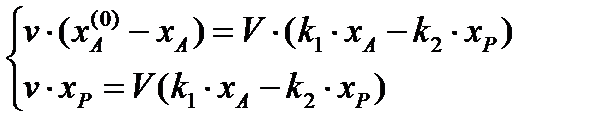
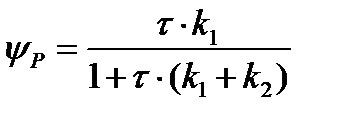
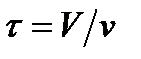 - среднее время пребывания реагентов в реакторе
- среднее время пребывания реагентов в реакторе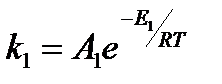
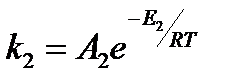
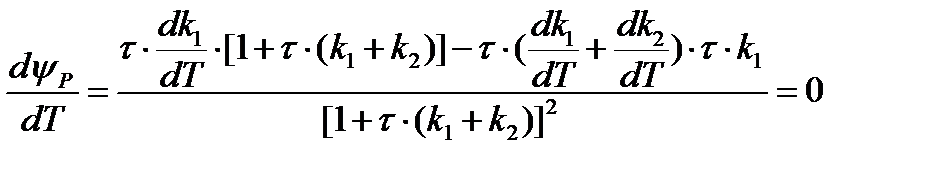
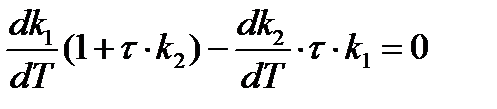 Учитывая, что:
Учитывая, что: 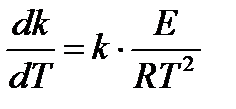
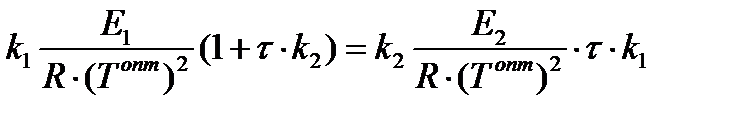
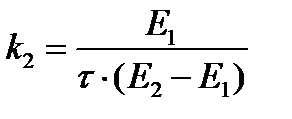 или
или 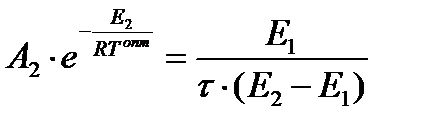
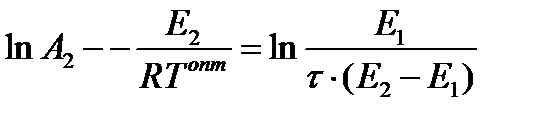 и
и 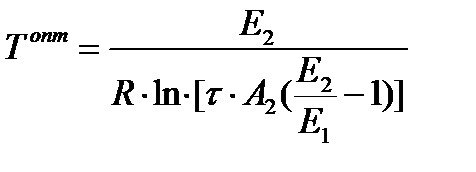
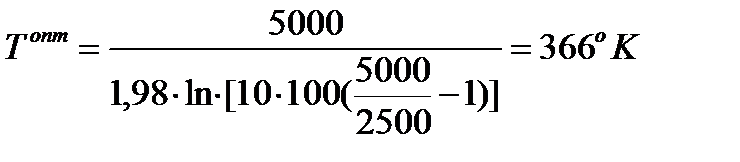
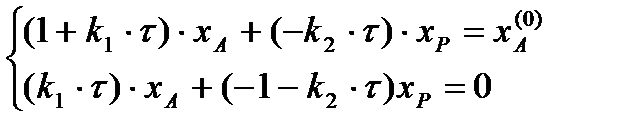
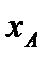 и
и 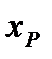 ) и
) и


