Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм метода Нелдера–МидаСодержание книги
Поиск на нашем сайте
где
где
Пусть – центр тяжести всех вершин, исключая
Тогда координаты этого центра тяжести определятся формулой: j – координатное направление
α > 0 – коэффициент отражения, – центр тяжести
2. Растяжение. Если , то вектор растягивается в соответствии с соотношением
Если , то заменяется на и процедура продолжается снова с операции 1 при k = k + 1.
В противном случае заменяется на и также осуществляется переход к операции 1 при k = k + 1.
3. Сжатие. Если для всех i ≠ h, то вектор
Затем заменяется на и происходит возврат к операции 1.
по формуле:
Критерий окончания поиска, использованный Нелдером и Мидом, имеет следующий вид: где ε – произвольное малое число Деформируемый многогранник адаптируется к топографии целевой функции, вытягиваясь вдоль длинных наклонных плоскостей, изменяя направление в изогнутых впадинах и сжимаясь в окрестности минимума.
Методы случайного поиска В основе методов случайного поиска лежит стратегия нахождения экстремума функции путем перебора совокупностей случайных значений независимых переменных. Эти методы, получившие общее название методов Монте-Карло, успешно применяются с использованием вычислительных машин для решения задач обращения матриц, нахождения собственных значений и собственных векторов матриц, решения систем алгебраических уравнений и целого ряда других задач. Общим для всех методов случайного поиска является генерирование и использование случайных чисел в процессе поиска, отличием – стратегия движения к экстремуму. Из методов случайного поиска наибольшее распространение получил метод случайного направления.
β i – компонент случайного вектора
Процедура генерирования случайного направления (вектора ) повторяется до тех пор, пока не будет найден экстремум функции
,что позволяет существенно сократить время поиска. Если и обратный шаг окажется неудачным, то можно из предыдущей точки сделать новый шаг, сгенерировав новый случайный вектор направления, или перейти к поиску с меньшим значением шага.
Прямые методы поиска экстремума функции многих переменных, использующие производные (методы первого порядка)
Методы оптимизации с использованием производных, как правило, более эффективны в смысле скорости сходимости, чем методы, не использующие производные. Однако, приближённый расчёт производных численными методами трудоёмок и трудно оценить погрешность полученных при этом результатов.
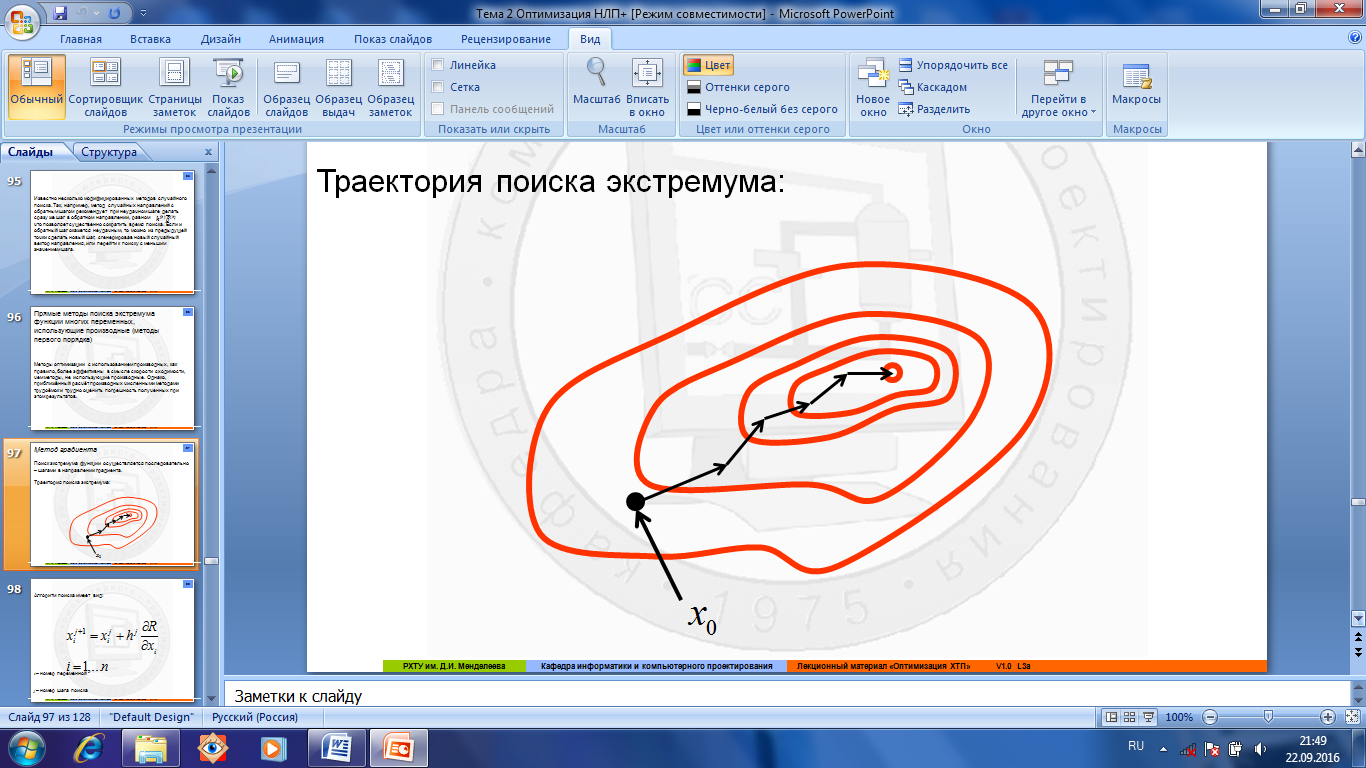
Рис.1.4.16. Последовательно – шагами в направлении градиента
снова вычисляется градиент функции
Величина h носит название фактора шага.
ε – заданная точность поиска
|
||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

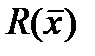
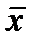
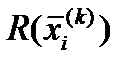
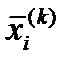
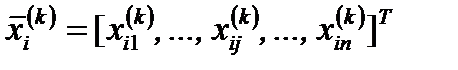 Пусть , i = 1, …, n + 1,является i – й вершиной (точкой в n – мерном пространстве En на k – м этапе поиска k = 0, 1, …, и пусть значение целевой функции в точке равно . Кроме того, отметим те векторы многогранника, которые дают максимальное и минимальное значения .
Пусть , i = 1, …, n + 1,является i – й вершиной (точкой в n – мерном пространстве En на k – м этапе поиска k = 0, 1, …, и пусть значение целевой функции в точке равно . Кроме того, отметим те векторы многогранника, которые дают максимальное и минимальное значения .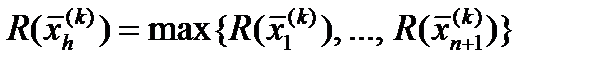 Определим
Определим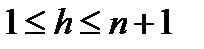
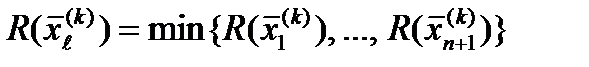 и
и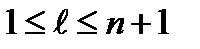
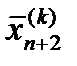
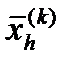
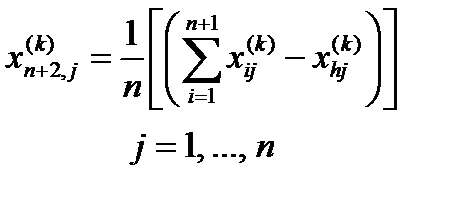
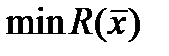 Начальный многогранник обычно выбирается в виде регулярного симплекса с точкой 1 в качестве начала координат. Процедура отыскания
Начальный многогранник обычно выбирается в виде регулярного симплекса с точкой 1 в качестве начала координат. Процедура отыскания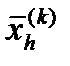 состоит из следующих 4 операций:
состоит из следующих 4 операций: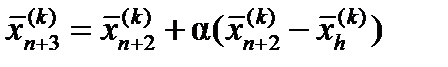 1. Отражение – проектирование через центр тяжести в соответствии с соотношением
1. Отражение – проектирование через центр тяжести в соответствии с соотношением 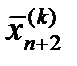
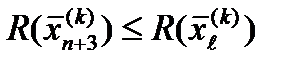
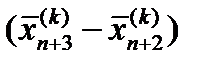
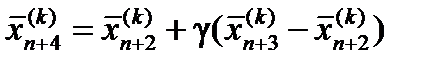 γ > 1 – коэффициент растяжения
γ > 1 – коэффициент растяжения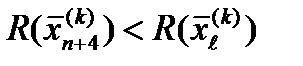
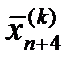
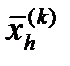
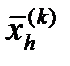
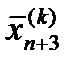
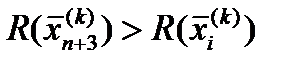
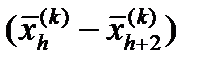
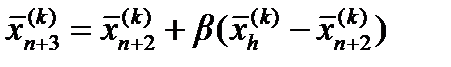 сжимается в соответствии с формулой:
сжимается в соответствии с формулой: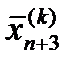
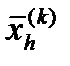 0 < β < 1 – коэффициент сжатия
0 < β < 1 – коэффициент сжатия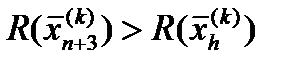
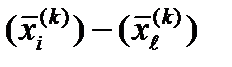
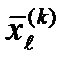 4. Редукция. Если , все векторы
4. Редукция. Если , все векторы 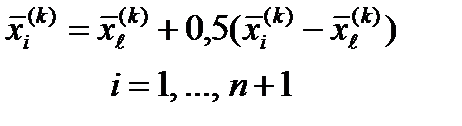 i = 1, …, n+1, уменьшаются в два раза с отсчетом от
i = 1, …, n+1, уменьшаются в два раза с отсчетом от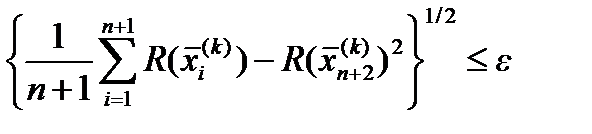 Затем осуществляется переход к операции 1.
Затем осуществляется переход к операции 1.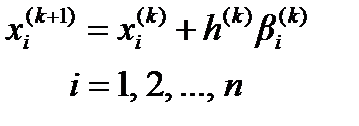 При использовании этого метода очередное приближение определяется соотношением:
При использовании этого метода очередное приближение определяется соотношением: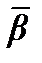 h ( k ) – параметр шага
h ( k ) – параметр шага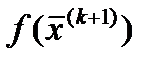
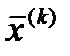
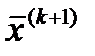
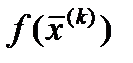 Если значение функции в новой точке оказывается меньше предыдущего , то в качестве очередного приближения принимаются последние значения неизвестных
Если значение функции в новой точке оказывается меньше предыдущего , то в качестве очередного приближения принимаются последние значения неизвестных 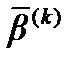 в противном случае остаются предыдущие значения
в противном случае остаются предыдущие значения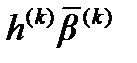 Известно несколько модифицированных методов случайного поиска. Так, например, метод случайных направлений с обратным шагом рекомендует при неудачном шаге делать сразу же шаг в обратном направлении, равном
Известно несколько модифицированных методов случайного поиска. Так, например, метод случайных направлений с обратным шагом рекомендует при неудачном шаге делать сразу же шаг в обратном направлении, равном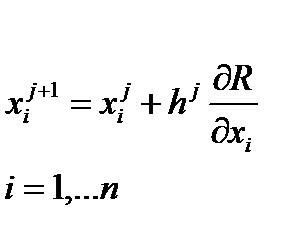 Метод градиентаПоиск экстремума (рис.1.4.16) функции осуществляется последовательно – шагами в направлении градиента.
i – номер переменной, j – номер шага поиска
Метод градиентаПоиск экстремума (рис.1.4.16) функции осуществляется последовательно – шагами в направлении градиента.
i – номер переменной, j – номер шага поиска
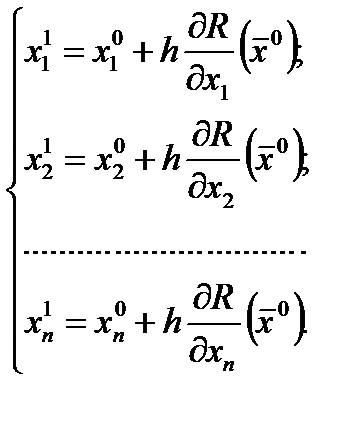
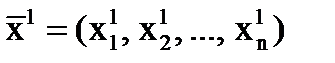 В начальной точке поиска вычисляется градиент функции, а затем находятся координаты положения точки
В начальной точке поиска вычисляется градиент функции, а затем находятся координаты положения точки 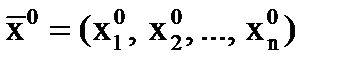
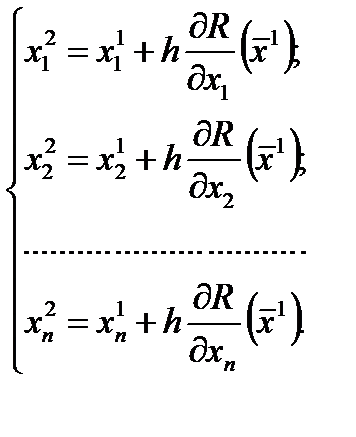
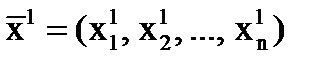 В полученной точке
В полученной точке 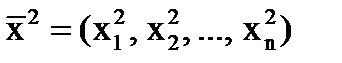 и находится точка
и находится точка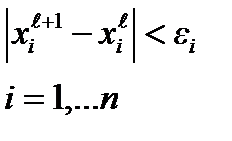 Процесс продолжается до тех пор, пока экстремум не будет найден с достаточной точностью, т.е. пока не будут выполнены неравенства:
Процесс продолжается до тех пор, пока экстремум не будет найден с достаточной точностью, т.е. пока не будут выполнены неравенства: