
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель системы безопасности hru. Основные положения Модели. Теорема об алгоритмической неразрешимости проблемы безопасности в произвольной системе.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Модель Харрисона-Рузо-Ульмана используется для анализа системы защиты, реализующей дискреционную политику безопасности, и ее основного элемента - матрицы доступов. При этом система защиты представляется конечным автоматом, функционирующим согласно определенным правилам перехода. Модель HRU была впервые предложена в 1971 г. В 1976 г. появилось формальное описание модели. Обозначим: О – множество объектов системы; S – множество субъектов системы (SÍO); R – множество прав доступа субъектов к объектам, например права на чтение (read), на запись (write), владения (own); M – матрица доступа, строки которой соответствуют субъектам, а столбцы -объектам; Отдельный автомат, построенный согласно положениям модели HRU, будем называть системой. Функционирование системы рассматривается только с точки зрения изменений в матрице доступа. Возможные изменения определяются шестью примитивными операторами: внести право, удалить право, создать субъекта, создать объект, уничтожить субъект, уничтожить объект. В результате выполнения примитивного оператора α осуществляется переход системы из состояния Q = (S,O,M) в новое состояние Однако, как показывают результаты анализа модели HRU, задача построения алгоритма проверки безопасности систем, реализующих дискреционную политику разграничения прав доступа, не может быть решена в общем случае. Обозначим состояние безопасности системы: Определение 1. Будем считать, что возможна утечка права rÎR в результате выполнения команды с, если при переходе системы в состояние Q' выполняется примитивный оператор, вносящий r в элемент матрицы доступов М, до этого r не содержавший. Определение 2. Начальное состояние Q0 называется безопасным по отношению к некоторому праву r, если невозможен переход системы в такое состояние О, в котором может возникнуть утечка права r. Теорема. Задача проверки безопасности произвольных систем алгоритмически неразрешима. Доказательство. Для доказательства теоремы воспользуемся фактом, доказанным в теории машин Тьюринга: не существует алгоритма проверки для произвольной машины Тьюринга и произвольного начального слова остановится ли машина Тьюринга в конечном состоянии или нет. Под машиной Тьюринга понимается способ переработки слов в конечных алфавитах. Слова записываются на бесконечную в обе стороны ленту, разбитую на ячейки. Суть: При сопоставлении машины Тьюринга и модели HRU, элементы и команды машины Тьюринга представляются в виде элементов и команд модели HRU. Зададим матрицу доступов М в текущем состоянии. Для каждой команды машины Тьюринга задается соответствующая ей команда модели HRU. Если машина Тьюринга останавливается в своем конечном состоянии, то в соответствующей системе, построенной на основе модели HRU, происходит утечка права доступа. Из алгоритмической неразрешимости задачи проверки - остановится ли машина Тьюринга в конечном состоянии, следует аналогичный вывод для задачи проверки безопасности соответствующей ей системы HRU. Таким образом, в общем случае для систем дискреционного разграничения доступа, построенных на основе модели HRU, задача проверки безопасности алгоритмически неразрешима. Дальнейшие исследования модели HRU велись в основном в направлении определения условий, которым должна удовлетворять система, чтобы для нее задача проверки безопасности была алгоритмически разрешима. Так, в 1976 г. было доказано, что эта задача разрешима для систем, в которых нет операции "создать". В 1978 г. показано, что таковыми могут быть системы монотонные и моноусловные, т.е. не содержащие операторов "уничтожить" или "удалить" и имеющие только команды, части условия которых имеют не более одного предложения. В том же году показано, что задача безопасности для систем с конечным множеством субъектов разрешима, но вычислительно сложна.
Модель распространения прав доступа Take-Grant. Теоремы о передаче прав в графе доступов, состоящем из субъектов, и произвольном графе доступов. Расширенная модель Take Grant и ее применение для анализа информационных потоков в АС.
Модель Take-Grant – это формальная модель, используемая в области компьютерной безопасности, для анализа систем дискреционного разграничения доступа; подтверждает либо опровергает степени защищенности данной автоматизированной системы, которая должна удовлетворять регламентированным требованиям. Модель представляет всю систему как направленный граф, где узлы - либо объекты, либо субъекты. Дуги между ними маркированы, и их значения указывают права, которые имеет объект или субъект (узел). В модели доминируют два правила: "давать" и "брать". Они играют в ней особую роль, переписывая правила, описывающие допустимые пути изменения графа. В общей сложности существует 4 правила преобразования: "брать", "давать", "создать", "удалить". Используя эти правила, можно воспроизвести состояния, в которых будет находиться система в зависимости от распределения и изменения прав доступа. Следовательно, можно проанализировать возможные угрозы для данной системы. Модель: О - множество объектов (файлы, сегменты памяти и т.д.) S - множество субъектов (пользователи, процессы системы) R = {r1, r2, r3, r4,..., rn } U {t,g} - множество прав доступа t [take] - право брать "права доступа" g [grant] - право давать "права доступа" G = (S, O, E) - конечный, помеченный, ориентированный граф без петель. × - объекты, элементы множества О • - субъекты, элементы множества S E ∈ O x O x R - дуги графа. Состояние системы описывается ее графом.
Правило "Брать" Брать = take(r, x, y, s), r ∈ R, Пусть s ∈ S, x,y ∈ O - вершины графа G Т.е. субьект S берет у объекта X права r на объект Y.
Правило "Давать" Давать = grant(r, x, y, s), r ∈ R, Пусть s ∈ S, x,y ∈ O - вершины графа G Т.е. субьект S дает объекту X права r на объект Y.
Правило "Создать" Создать = create(r, x, s), r ∈ R, Пусть s ∈ S, x,y ∈ O - вершины графа G
Удалить = remove(r, x, s), r ∈ R, Пусть s ∈ S, x,y ∈ O - вершины графа G
Теоремы о передаче прав в графе доступов, состоящем из субъектов, и произвольном графе доступов. В модели Take-Grant основное внимание уделяется определению условий, при которых в системе возможно распространение прав доступа определенным способом. • способа санкционированного получения прав доступа; • способа похищения прав доступа.
|
||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 1360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.134.196 (0.006 с.) |

 - права доступа субъекта s к объекту о.
- права доступа субъекта s к объекту о. . Данный переход обозначим через Q├aQ'. Из примитивных операторов могут составляться команды, каждая из которых состоит из двух частей: условия, при котором выполняется команда, последовательности примитивных операторов.
. Данный переход обозначим через Q├aQ'. Из примитивных операторов могут составляться команды, каждая из которых состоит из двух частей: условия, при котором выполняется команда, последовательности примитивных операторов.

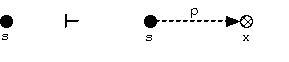
 Правило "Удалить"
Правило "Удалить"


