
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы шифрования с открытыми ключами: RSA, системы Эль-Гамаля, системы на основе «проблемы рюкзака».
Концепция криптографии с открытым ключом заключается в том, что для зашифрования и расшифрования используются разные ключи: открытый (публичный) и закрытый (секретный), причем зная значание открытого ключа нельзя (достаточно сложно) получить значение закрытого. RSA. Общая схема алгоритма: 1) каждый пользователь генерирует пару ключей: один для зашифрования и один для расшифрования; 2) пользователи публикуют свои ключи зашифрования в открытом доступе, а второй ключ, соответствующий открытому, сохраняетеся в секрете; 3) посылая пользователю В сообщение, пользователь А зашифровывает его открытым ключам пользователя В; 4) пользователь В расшифровывает полученное сообщение с помощью своего секретного ключа. Пользователь выбирает простые числа В зависимости от поставленной задачи (шифрование / ЭЦП), один из ключей засекречивается, а второй помещается в общий доступ. Криптостойкость данной системы основана на сложности разложения числа ElGamal. Безопасность алгоритма основана на трудности вычисления дискретных логарифмов в конечном поле. Для генерации пары ключей сначала выбирается простое число Система на основе «проблемы рюкзака». Безопасность алгоритмов рюкзака опирается на проблему рюкзака, NP -полную проблему. Проблема рюкзака заключается в следующем: пусть дан набор значений M1,M2,…,Mn и сумма S. Необходимо найти значения bi такие, что:
В основе алгоритма рюкзака Меркла-Хеллмана (оригинальной схемы на принципе рюкзака) лежит идея шифровать сообщение, как решение набора проблем рюкзака. Сверхвозрастающая последовательность рюкзака является закрытым ключам, а нормальная – открытым. Для шифрования данных используется нормальная последовательность, которая получается из сверхвозрастающей следующим образом: Для шифрования данные разбиваются на блоки по n бит. Считается сумма Для расшифрования необходимо знать числа Реальные рюкзаки должны содержать не менее 250 элементов. Длина каждого члена сверхвозрастающей последовательности должна быть где-то между 200 и 400 битами, а длина модуля должна быть от 100 до 200 битов. В таком случае, полный перебор для взлома будет бессмысленным. На сегодняшний день существуют алгоритмы достаточно быстрого взлома оригинальной схемы и большинства её модификаций. Также есть варианты алгоритма рюкзака, считающиеся безопасными на сегодняшний день.
Цифровая подпись. Общие положения. Цифровые подписи на основе шифросистемы с открытыми ключами стандартов ГОСТ Р и DSS. Электронная подпись - информация в электронной форме, которая присоединена к другой информации в электронной форме (подписываемой информации) или иным образом связана с такой информацией и которая используется для определения лица, подписывающего информацию. (Федеральный закон от 6 апреля 2011 г. N 63-ФЗ "Об электронной подписи") ЭЦП для сообщения является числом, зависящим от самого сообщения и от секретного ключа, известного только подписывающему. Важное требование: подпись должна допускать проверку без знания секретного ключа. При возникновении спорной ситуации, связанной с отказом от факта подписи либо с возможной подделкой подписи, третья сторона должна иметь возможность разрешить спор. Цифровая подпись позволяет решить следующие задачи: - аутентификация источника сообщения, - проверка целостности сообщения, - обеспечение невозможности отказа от факта подписи конкретного сообщения. Для реализации схемы ЭЦП необходимы: алгоритм генерации подписи и алгоритм проверки. Надежность схемы цифровой подписи определяется сложностью следующих трех задач: - подделки подписи, то есть нахождения значения подписи под заданным документом лицом, не являющимся владельцем секретного ключа; - создания подписанного сообщения, то есть нахождения хотя бы одного сообщения с правильным значением подписи; - подмены сообщения, то есть подбора двух различных сообщений с одинаковыми значениями подписи. Принципиальные подходы к созданию схем подписи: подпись на основе систем шифрования с открытыми ключами; схемы со специально разработанными алгоритмами вычисления и проверки подписи; схемы на основе симметричных систем шифрования. В н. в. наиболее широкое применение нашли подходы первого принципа. Наиболее распространенным является подход, использующий бесключевые хеш-функции. Для исключения возможности подмены злоумышленником открытого ключа (с целью подделки подписи), используется инфраструктура открытых ключей. DSS (Digital Signature Standard) – Американский стандарт цифровой подписи, использующий алгоритм DSA. Данный алгоритм представляет собой вариант подписи ElGamal. Выбирается простое число Выработка ЭЦП: считается хеш-функция Проверка ЭЦП: вычисляются числа: ГОСТ Р 34.10-2001 – российский стандарт, описывающий алгоритмы формирования и проверки электронной цифровой подписи. Стойкость применяемой в стандарте схемы цифровой подписи основывается на сложности решения задачи дискретного логарифмирования в группе точек эллиптической кривой, а также на стойкости используемой хэш-функции. Используемые параметры: — простое число
— эллиптическая кривая E, задается своим инвариантом J(E) или коэффициентами — целое число — простое число q - порядок некоторой циклической подгруппы группы точек эллиптической кривой, то есть выполняется m=nq, для некоторого — точка — h(M) — хэш-функция (ГОСТ Р 34.11-94), отображает сообщения M в двоичные векторы длины 256 бит. Ключ шифрования: d-целое число, лежащее в пределах 0<d<q; ключ расшифрования: Дополнительные требования:
|
|||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 629; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.250.1 (0.018 с.) |
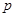 и
и 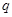 , вычисляет
, вычисляет  и выбирает число
и выбирает число 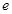 (- ключ шифрования), взаимно простое с
(- ключ шифрования), взаимно простое с 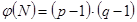 , где
, где 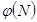 - функция Эйлера. Далее находим число
- функция Эйлера. Далее находим число  (- ключ расшифрования),обратное относительно умножения к
(- ключ расшифрования),обратное относительно умножения к  . Шифрующее преобразование:
. Шифрующее преобразование:  , расшифровывающее преобразование:
, расшифровывающее преобразование: 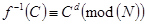 . Легко заметить, что
. Легко заметить, что 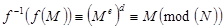
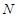 на простые множители
на простые множители 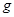 и
и 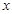 :
: 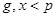 . Затем вычисляется
. Затем вычисляется  . Открытым ключом являются
. Открытым ключом являются  ,
,  , взаимно простое с
, взаимно простое с 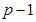 . Затем вычисляются
. Затем вычисляются  и
и  . Пара
. Пара 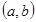 является закрытым шифртекстом. Для расшифрования
является закрытым шифртекстом. Для расшифрования 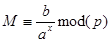 . Проверяем:
. Проверяем: 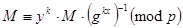 ,
, 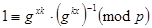 .
.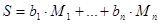 , где
, где  может быть либо нулем, либо единицей. Существует 2 проблемы рюкзака. Проблема рюкзака является «Легкой», если перечень значений (Mi) представляет собой сверхвозрастающую последовательность (когда каждый член больше суммы всех предыдущих). Решение заключается в сравнении суммы (S) с самым большим числом последовательности. Если S больше, либо равен этому числу (Mi), то bi принимают за «1». Уменьшаем S на значение Mi и переходим к следующему числу последовательности. Процесс повторяется, пока последовательность не закончится. Если по окончании S равно нулю, то решение найдено. Проблема рюкзака является «Трудной», если перечень значений (Mi) – не сверхвозрастающая или нормальная последовательность. Алгоритма быстрого решения не найдено.
может быть либо нулем, либо единицей. Существует 2 проблемы рюкзака. Проблема рюкзака является «Легкой», если перечень значений (Mi) представляет собой сверхвозрастающую последовательность (когда каждый член больше суммы всех предыдущих). Решение заключается в сравнении суммы (S) с самым большим числом последовательности. Если S больше, либо равен этому числу (Mi), то bi принимают за «1». Уменьшаем S на значение Mi и переходим к следующему числу последовательности. Процесс повторяется, пока последовательность не закончится. Если по окончании S равно нулю, то решение найдено. Проблема рюкзака является «Трудной», если перечень значений (Mi) – не сверхвозрастающая или нормальная последовательность. Алгоритма быстрого решения не найдено.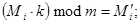 Здесь
Здесь  - член сверхвозрастающей последовательности,
- член сверхвозрастающей последовательности, 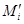 - полученный член нормальной последовательности для шифрования,
- полученный член нормальной последовательности для шифрования,  - число, большее суммы элементов сверхвозрастающей последовательности, k- число, взаимно простое с
- число, большее суммы элементов сверхвозрастающей последовательности, k- число, взаимно простое с  , которая является шифрованным текстом. Нормальная последовательность
, которая является шифрованным текстом. Нормальная последовательность 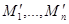 является открытым ключом шифрования.
является открытым ключом шифрования.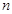 и
и 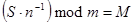 , где
, где 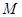 преобразуется алгоритмом расшифровки сверхвозрастающего рюкзака в исходную последовательность бит.
преобразуется алгоритмом расшифровки сверхвозрастающего рюкзака в исходную последовательность бит.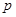 длиной L битов, где L принимает значение, кратное 64, в диапазоне от 512 до 1024. Выбирается простое число
длиной L битов, где L принимает значение, кратное 64, в диапазоне от 512 до 1024. Выбирается простое число  - (множитель р-1) длиной 160 бит. Выбирается
- (множитель р-1) длиной 160 бит. Выбирается 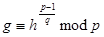 , где
, где  - любое число, меньшее
- любое число, меньшее 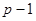 , такое что
, такое что 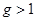 .
. 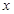 - закрытый ключ
- закрытый ключ 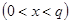 ,
, 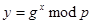 - открытый ключ. Параметры
- открытый ключ. Параметры 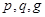 - открыты и могут быть общими для группы пользователей.
- открыты и могут быть общими для группы пользователей. (хеш-код сообщения М по методу SHA-1), генерируется случайное
(хеш-код сообщения М по методу SHA-1), генерируется случайное 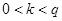 , вычисляются:
, вычисляются: 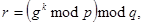
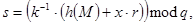 которые являются подписью.
которые являются подписью.
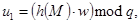
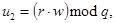
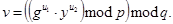 Если
Если 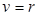 , то подпись верна.
, то подпись верна.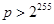 — модуль эллиптической кривой;
— модуль эллиптической кривой; , где Fp — конечное поле из p элементов.
, где Fp — конечное поле из p элементов.  , причем
, причем 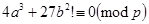 (значит не тождественно);
(значит не тождественно);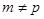 — порядок группы точек эллиптической кривой;
— порядок группы точек эллиптической кривой; .
. 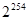 <q<
<q< 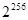 ;
;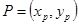 эллиптической кривой E, являющаяся генератором подгруппы порядка q, то есть
эллиптической кривой E, являющаяся генератором подгруппы порядка q, то есть 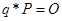 и
и 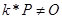 для всех k = 1, 2, …, q-1, где
для всех k = 1, 2, …, q-1, где 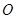 — нейтральный элемент группы точек эллиптической кривой E;
— нейтральный элемент группы точек эллиптической кривой E; вычисляемый как
вычисляемый как 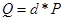 .
. где
где  ;
; 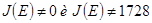 (пожалуй можно забыть, взято из госта)
(пожалуй можно забыть, взято из госта)


