Формирование цифровой подписи

1.Вычисление хэш-функции от сообщения М: ;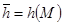

2.Вычисление e=z mod q, и если e=0, положить e=1. Где z — целое число, соответствующее (т.е. - это двоичное представление числа z);

3.Генерация случайного числа k такого, что 0<k<q;

4.Вычисление точки эллиптической кривой C=kP, и по ней нахождение , где — это координата x точки C. Если r=0, возвращаемся к предыдущему шагу;

5.Нахождение s=(rd+ke) mod q. Если s=0, возвращаемся к шагу 3;

6.Формирование цифровой подписи , где и — векторы, соответствующие r и s.

Проверка цифровой подписи

1.Вычисление по цифровой подписи чисел r и s, учитывая, что , где r и s — числа, соответствующие векторам и . Если хотя бы одно из неравенств r<q и s<q неверно, то подпись неправильная;

2.Вычисление хэш-функции от сообщения М: ;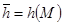

3.Вычисление e=z mod q, и если e=0, положить e=1. Где z — целое число соответствующее ;

4.Вычисление ;

5.Вычисление и ;

6.Вычисление точки эллиптической кривой . И определение , где — координата x кривой C;

7.В случае равенства R=r подпись действительная, иначе — фальшивая.

 

 

 

Функции хэширования. Требования предъявляемые к функциям хэширования. Ключевые функции хэширования. Безключевые функции хэширования.

Хеш-функции – это функции, предназначенные для «сжатия» произвольного сообщения или набора данных в битовую комбинацию фиксированной длины, называемую сверткой.

Функцией хэширования называется функция h, удовлетворяющая минимум двум требованиям:

Сжатие – функция h отображает входное сообщение x (прообраз) произвольной длины в хэш-значение y=h(x) небольшой фиксированной длины.

Простота вычисления – для заданной функции h и сообщения x, h(x) вычисляется не выше чем с полиномиальной сложностью.

Хэш-функции применяются в статистических экспериментах, для проверки целостности, в алгоритмах индексированного поиска данных; в криптографии: в системах контроля целостности данных, при аутентификации источника, номера, времени сообщения (хеширование паролей).

Свойства хэш-функций:

Однонаправленность – вычислительная сложность нахождения неизвестного прообраза для предварительно заданного хэш-значения.

Стойкость к вычислению второго прообраза – сложность нахождения любого другого прообраза, который давал бы такое же хэш-значение, как и заданный.

Стойкость к коллизиям – сложность нахождения двух прообразов, для которых вырабатывалось бы одинаковое значение.

Свойства 1 и 2 предотвращают воздействия злоумышленника на канал связи (препятствуют подмене, изменению и посылке ложных сообщений злоумышленником от лица отправителя), свойство 3 не допускает ситуацию, когда абонент 1 подбирает абоненту 2 на подпись два договора с одинаковым значением хэш-функции: «нормальный» и «невыгодный» для абонента 2, но выгодный для себя. Абонент 2 подписывает «нормальный» договор, т.о. абонент 1 получает подпись и для «невыгодного» договора.

Алгоритм хеширования должен быть открытым.

Особо выделяют два важных типа хеш-функций: