
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выделение компонент связности в неориентированном графе
Этап 1(первоначальная разметка): Шаг 1. Пометить все вершины графа маркером «1»; Шаг 2. Пометить любую вершину с маркером «1» маркером «2»; Этап 2 (разметка соседних вершин): Шаг 3. Если нет вершин, помеченных маркером «2» - переходим к этапу 3; Шаг 4. Выбираем любую вершину с маркером «2», помечаем ее маркером «3», а все соседние вершины, помеченные маркером «1», помечаем маркером «2». Затем повторяем этот этап сначала; Этап 3 (сбор результатов): Шаг 5. Если нужно получить список вершин, входящих в одну компоненту связности с заданной вершиной, то выбираем вершины, помеченные третьим маркером; Шаг 6. Если нужно получить список вершин, не входящих в одну компоненту связности с заданной вершиной, то выбираем вершины, помеченные маркером «1»; Шаг 7. Если нужно просто проверить граф на связность, то считаем вершины, помеченные первым маркером, и сравниваем получившееся число с нулем. Если число вершин, помеченных первым маркером, равно нулю, то граф связный. Выделение компонент сильной связности в орграфе Этап 1(первоначальная разметка): Шаг 1. Пометить все вершины графа маркером «1»; Шаг 2. Пометить любую вершину с маркером «1» маркером «2»; Этап 2 (разметка соседних вершин): Шаг 3. Если нет вершин, помеченных маркером «2» и все вершины в графе помечены маркером «Di» - переходим к этапу 3. Если нет вершин, помеченных маркером «2», но есть вершины с маркером «1» и без маркера «Di», то i = i + 1 и переходим к шагу 2. Если есть вершина с маркером «2», переходим к шагу 4; Шаг 4. Выбираем любую вершину v с маркером «2», помечаем ее маркером «3» и маркером «Di» (если она еще не помечена маркером «Di») (здесь i - номер компоненты связности), а все соседние вершины u, достижимые из этой вершины и помеченные маркером «1», помечаем маркером «2». Если нет достижимых соседних вершин с маркером «1», то повторяем этап 2. Шаг 5. Проверяем, есть ли путь из вершины u обратно в вершину v. Если есть – помечаем вершину u маркерами «3» и «Di». Если нет – снова помечаем вершину u маркером «1». Затем повторяем этот этап сначала; Этап 3 (сбор результатов): Шаг 6. Если нужно получить список вершин, входящих в одну компоненту связности с заданной вершиной, то выбираем вершины, помеченные соответствующим маркером «Di»; Шаг 7. Если нужно получить список вершин, не входящих в компоненту связности «Di» то выбираем вершины, помеченные маркером, отличным от маркера «Di»;
Таким образом, результатом данного алгоритма будут: а) количество компонент сильной связности; б) сгруппированные по компонентам связности вершины орграфа; Поиск в ширину и кратчайшие пути в графе Поиск в ширину находит расстояния до каждой достижимой вершины в графе от исходной вершины s. Определим длину кратчайшего пути δ(s,v) как минимальное количество ребер на пути от s к v, если пути не существует, то δ(s,v) = ∞. CСледующий алгоритм вычисляет длины кратчайших путей. 1. Пусть G=(V,E) – ориентированный или неориентированный граф, а s – его произвольная вершина, тогда для любого ребра (u,v) графа справедливо δ(s,v) ≤ δ(s,u)+1. 2. Пусть в данном графе процедура поиска (//обхода) в ширину выполняется с исходной вершиной s. Тогда по завершении процедуры для каждой вершины графа v справедливо d[v] ≥ δ(s,v). Где d[v] – метка времени, показывающая, на каком шаге алгоритма обхода в ширину была достигнута вершина v. По сути – расстояние от v до s. 3. Следствием выполнения процедуры поиска в ширину над графом G=(V,E) является монотонное увеличение параметра d, при каждом следующем шаге алгоритма обхода в ширину. 4. Таким образом, в процессе своей работы алгоритм обхода в ширину открывает все вершины v ∈ V, достижимые из s, и по окончании работы алгоритма для каждой vi∈V будет справедливо d[vi]= δ(s,v). Кроме того, для всех достижимых из s вершин v ≠ s, один из кратчайших путей от s к v – это путь от s к π[v], за которым следует ребро (π[v], v), где π[v] – вершина, из которой мы попали в вершину v, в процессе процедуры поиска в ширину.
Системы линейного уравнения над кольцом и полем. Системы линейных уравнений над коммутативным кольцом с единицей. Равносильность систем. Системы уравнений над кольцом. Однородные уравнения и функциональная система решений. Введём понятие кольца и поля Кольцо — это множество М с двумя бинарными операциями 1. 2. 3.
4. 5. 6. Кольцо называется коммутативным, если 7. Коммутативное кольцо называется кольцом с единицей, если 8. Поле — это множество М с двумя бинарными операциями 1. 2. 3. 4. 5. 6. 7. 8. 9. Определим понятие системы линейных уравнений В общем случае система
При этом через Система (3.1) называется однородной, если все ее свободные члены Если хотя бы один из свободных членов Система (3.1) называется квадратной, если число т составляющих ее уравнений равно числу неизвестных п. Решением системы (3.1) называется такая совокупность Система уравнений вида (3.1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее не существует ни одного решения. Совместная система вида (3.1) может иметь или одно решение, или несколько решений. Два решения совместной системы вида
Совместная система вида (3.1) называется определенной, если она имеет единственное решение. Совместная система вида (3.1) называется неопределенной, если у нее существуют по крайней мере два различных решения. Для произвольного основного поля Р остаются справедливыми метод Гаусса для решения систем линейных уравнений, теория определителей и правило Крамера. Полностью переносятся на случай произвольного основного поля теория линейной зависимости векторов, теория ранга матрицы и общая теория систем линейных уравнений, а также алгебра матриц. Теорема Кронекера-Капелли: система линейных уравнений тогда и только тогда совместна, когда ранг расширенной матрицы В равен рангу матрицы А. Рассмотрим всевозможные упорядоченные конечные системы элементов поля Р, имеющие вид: (а0, а1, …, аn-1, аn) (1), причем n произвольно, n≥0, но при n>0 должно быть an≠0. Определяя для систем вида (1) сложение и умножение в соответствии с формулами: Если даны многочлены f(x) и g(x) с комплексными коэффициентами, записанные для удобства по возрастающим степеням х: f(x)=a0 + a1x + … + an-1xn-1 + anxn, an≠0 g(x)=b0 + b1x + …+ bs-1xs-1 + bsxs, bs≠0 и если, например, n>=s, то их суммой называется многочлен f(x)+g(x)=c0+c1x+…+cs-1xs-1+csxs , где ci=ai+bi, i=0,1, …,n. причем при n>s коэффициенты bs+1 bs+2,..., bп следует считать равными нулю. Степень суммы будет равна n, если n больше s, но при n=s она может случайно оказаться меньше n, а именно в случае b„== - ап. Произведением многочленов f{x) и g{x) называется многочлен
f(x)*g(x)=d0+d1x+…+dn+s-1xn+s-1+dn+sxn+s , где di= т. е. коэффициент dt есть результат перемножения таких коэффициентов многочленов /(х) и g(x), сумма индексов которых равна i, и сложения всех таких произведений; поэтому степень произведения двух многочленов равна сумме степеней этих многочленов. Отсюда следует, что произведение многочленов, отличных от нуля, никогда не будет равным нулю. Какими свойствами обладают введенные нами операции для многочленов? Коммутативность и ассоциативность сложения немедленно вытекают из справедливости этих свойств для сложения чисел, так как складываются коэффициенты при каждой степени неизвестного отдельно. Вычитание оказывается выполнимым: роль нуля играет число нуль, включенное нами в число многочленов, а противоположным для записанного выше многочлена f(х) будет многочлен -f(x) = — а0—а1х—... —an-1xn-1—anxn Коммутативность умножения вытекает из коммутативности умножения чисел и того факта, что в определении произведения многочленов коэффициенты обоих множителей f(x) и g(x) используются совершенно равноправным образом. Ассоциативность умножения доказывается следующим образом: если, помимо записанных выше многочленов f(х) и g{x), дан еще многочлен h(x)=c0 + c1x + …+ ct-1xt-1 + ctxt, ct≠0 то коэффициентом при хi, i = 0, 1,..., n+s+t в произведении [f(x)g(x)]h(x) будет служить число
в произведении f(x)[g(x)h(x)] — равное ему число
Наконец, справедливость закона дистрибутивности вытекает из равенства
так как левая часть этого равенства является коэффициентом при Xi в многочлене [f(x)+g(x)]h(x), а правая часть —коэффициентом при той же степени неизвестного в многочлене f(x)h{x) + g(x)h(x). Заметим, что роль единицы при умножении многочленов играет число 1, рассматриваемое как многочлен нулевой степени. С другой стороны, многочлен f(x) тогда и только тогда обладает обратным многочленом f-1(х), f(x) f-1(х) = 1, если f{x) является многочленом нулевой степени. Действительно, если f(x) является отличным от нуля числом а, то обратным многочленом служит для него число а-1. Если же f(x) имеет степень n>=1, то степень левой части равенства f(x) f-1(х) = 1, если бы многочлен f-1(х) существовал, была бы не меньше n, в то время как справа стоит многочлен нулевой степени. Правило решения произвольной системы линейных уравнений: пусть дана совместная система линейных уравнений 3.1 и пусть матрица из коэффициентов А имеет ранг r. Выбираем в А r линейно независимых строк и оставляем в системе 3.1 лишь уравнения, коэффициенты которых вошли в выбранные строки. В этих уравнениях оставляем в левых частях такие r неизвестных, что определитель при коэффициентах при них отличен от нуля, а остальные неизвестные объявляем свободными и переносим в правые части уравнений. Давая свободным неизвестным произвольные числовые значения и вычисляя значения остальных неизвестных по правилу Крамера, мы получим все решения системы.
Докажем что квадратная система линейных уравнений (3.10) с определителем основной матрицы, отличным от нуля, имеет, и притом единственное, решение, определяемое формулами Крамера (1) В случае, когда дана системы линейного уравнения над кольцом с определителем основной матрицы, отличным от нуля кольца, эта система имеет и притом единственное, решение, определяемое формулами Крамера Теорема. Квадратная матрица М над кольцом Доказательство (1) Пусть дана квадратная система линейных уравнений
с отличным от нуля определителем
Докажем, что система (3.10) может иметь только одно решение (т. е. докажем единственность решения системы (3.10) в предположении его существования). Предположим, что существуют какие-либо п чисел
Учитывая, что сумма произведений элементов
Обозначим символом Заметим, что в правой части (3.12) стоит именно определитель
Поскольку определитель
Итак, мы доказали, что если решение с определителем Формулы (3.14) называются формулами Крамера 10). Еще раз подчеркнем, что формулы Крамера пока получены нами в предположении существования решения и доказывают его единственность. Остается доказать существование решения системы (3.10). Для этого в силу теоремы Кронекера-Капелли достаточно доказать, что ранг основной матрицы (3.11) равен рангу расширенной матрицы п)
но это очевидно, ибо в силу соотношения
Равносильность. Два многочлена f(x) и g(x) будут считаться равными (или тождественно равными), f(x)=g(x), если равны их коэффицменты при одинаковых степенях неизвестного. Пусть матрица А из коэффициентов системы однородных ЛУ имеет ранг r. Если r=n, то нулевое решение будет единственным решением однородной СЛУ. При r<n система обладает также решениями, отличными от нулевого, и для разыскания всех этих решений применяется тот же прием, как выше в случае произвольной системы уравнений. В частности, система n линейных однородных уравнений с n неизвестными тогда и только тогда обладает решениями, отличными от нулевого, если определитель этой исстемы равен нулю. Если в системе однородных уравнений число уравнений меньше числа неизвестных, то система непременно обладает решениями, отличными от нулевого, т.к. ранг в данном случае не может быть равным числу неизвестных. Поэтому вообще всякая линейная комбинация решений однородной системы будет сама решением этой системы. Но в случае неоднородной системы, т.е. системы линейных уравнений, свободные члены которых (правые части) не все равны 0, соответствующее утверждение не имеет места: ни сумма двух решений системы неоднородных уравнений, ни произведение решения этой системы на число не будут решениями для этой системы. Известно, что всякая система n-мерных векторов, состоящая более чем из n векторов, будет линейно зависимой. Отсюда следует, что из числа решений однородной системы, являющихся n-мерными векторами, можно выбрать конечную максимальную линейно независимую систему, максимальное в том смысле, что всякое другое решение однородной СЛУ будет линейной комбинацией решений, входящих в эту выбранную систему. Всякая максимальная линейно независимая система решений однородной СЛУ называется ее фундаментальной системой решений. Фундаментальная система решений будет существовать лишь в том случае, если система однородных ЛУ обладает ненулевыми решениями, т.е. если ранг ее матрицы из коэффициентов меньше числа неизвестных. При этом система однородных ЛУ может обладать многими различными фундаментальными системами решений. Все эти системы эквивалентны между собой, т.к. каждый вектор всякой из этих систем линейно выражается через любую другую систему, поэтому системы состоят из одного и того же числа решений. Теорема: если ранг r матрицы из коэффициентов системы линейных однородных уравнений меньше числа неизвестных n, то всякая фундаментальная система решений этой СЛУ состоит из n-r решений. Алгоритмы на графах. Обход графа в глубину, построение глубинного остового леса и классификация ребер, не вошедших в лес. Алгоритмы нахождения связных компонентов неориентированных графов и сильно связных компонентов ориентированных графов. Поиск в ширину и кратчайшие пути в графе. Обход графа в глубину – метод систематического прохождения (посещения) вершин графа, когда за счет продвижений от текущей вершины по ребру вперед (к еще непросмотренной вершине) всегда, когда это возможно, и возвратов от текущей вершины по пройденному ребру назад (к ранее пройденной вершине), если движение вперед от текущей вершины невозможно, осуществляется движение по всем вершинам графа, достижимым из заданной вершины s, с которой начинается поиск. Поиск в глубину всегда завершается через конечное число шагов в вершине s - начале просмотра. Осуществляется по следующим правилам: (1) находясь в вершине x, нужно двигаться в любую другую, ранее непосещенную вершину (если таковая найдется), одновременно запоминая дугу, по которой мы впервые попали в данную вершину; Остовное дерево связного графа Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом Пусть G — связный граф. Тогда в силу утверждения 4.35 остовное дерево графа G (если оно существует) должно содержать n(G) — 1 ребер. Таким образом, любое остовное дерево граф! есть результат удаления из G ровно m(G) — (n(G) -= m(G) — n{G) + 1 ребер. Число m(G) — n(G) + 1 называется цикломатическим чис лом связного графа G и обозначается через v(G). Покажем существование остовного дерева для произвольного связного псевдографа G = (V, X), описав алгоритм его выделения. Алгоритм 4.6: Шаг 1. Выбираем в G произвольную вершину иг, которая _ разует подграф Gi псевдографа G, являющийся деревом. Пол гаем t= 1. Шаг 2. Если i = п, где п = n(G), то задача решена, и G, искомое остовное дерево псевдографа G. В противном случае п реходим к шагу 3. Шаг 3. Пусть уже построено дерево Gi, являющееся подграфом псевдографа G и содержащее некоторые вершины u1,...ui, где 1 <i<n- 1. Строим граф Gi+i, добавляя к графу G; новую вершину Ui+iЭV, смежную в G с некоторой вершиной uj графа Gi,-, и новое ребро {ui+1, u j} (в силу связности G и того обстоятельства, что i<n, указанная вершина ui+1 обязательно найдется). Согласно утверждению 4.36 граф Gi+1 также является деревом. Присваиваем i: =i+l и переходим к шагу 2. Выделение компонент связности Опишем алгоритм нахождения числа компонент сильной связности орграфа, а также выделения этих компонент. Аналогичным образом решается задача нахождения количества компонент связности, а также выделения компонент связности неориентированного графа. Однако для определенности приводим рассуждения для орграфа. Воспользуемся следующими утверждениями. Утверждение 4.18. Пусть D — орграф с р≥2 компонентами сильной связности: D1...,DP. Тогда в результате удаления из D вершин, содержащихся в D1 получаем орграф с р —1 компонентами сильной связности: D2..., Dp. -Воспользуемся тем очевидным фактом, что если D' — компонента сильной связности орграфа D, то D' является компонентой сильной связности и любого подграфа орграфа D, содержащего все вершины и дуги орграфа D'. Используя утверждение Утверждение 4.11. Пусть D = (V, X) — ориентированный псевдограф с р компонентами сильной связности: D1 = (V1, Х1),..., DP = (VP, Xp). Тогда 1) V=ViU..UV,, X=>X1U...UXp; 2) ViЛVj =Ø, XiЛXj=Ø при i≠j, 3) n(ni)+...+n(Dp)=n(D),m(Dl)+...+m(Dp)≤ m(D). Утверждение 4.19. Пусть D' — компонента сильной связности орграфа D. Пусть также p(D)≥2 и D" — орграф, получаемый в результате удаления из D вершин, содержащихся в D', Тогда матрицами A(D"), S(D") являются подматрицы матриц A(D), S(D), получаемые в результате удаления из них строк и столбцов, соответствующих вершинам орграфа D'. Утверждение 4.19 является следствием утверждений 4.18 и 4.14. Из определения матрицы сильной связности вытекает, что справедливо Утверждение 4.20. Единицы i-й строки или i-го столбца матрицы сильной связности орграфа D = (V, X), где V={vx,..., vn), соответствуют вершинам компоненты сильной связности орграфа D, содержащей вершину vi. Из утверждений 4.18—4.20 следует справедливость алгоритма определения числа компонент сильной связности орграфа D, а также матриц смежности этих компонент. Алгоритм 4.1: Шаг 1. Полагаем р = 1, Si=S(D). Шаг 2. Включаем в множество вершин Vp очередной компоненты сильной связности Dp орграфа D вершины, соответствующие единицам первой строки матрицы Sp. В качестве A (Dp) берем подматрицу матрицы A(D), находящуюся на пересечении строк и столбцов, соответствующих вершинам из Vp. Шаг 3. Вычеркиваем из Sp строки и столбцы, соответствующие вершинам из Vp. Если в результате такого вычеркивания не остается ни одной строки (и соответственно ни одного столбца), то р —количество компонент сильной связности и A (Di),......, A (Dp) — матрицы смежности компонент сильной связности Di,..., Dp орграфа D. В противном случае обозначаем оставшуюся после вычеркивания из Sp соответствующих строк и столбцов матрицу через Sp+1, присваиваем р: =р+1 и переходим к шагу 2.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 744; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.218.254 (0.083 с.) |
 в котором:
в котором: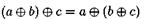 сложение ассоциативно;
сложение ассоциативно; существует нуль;
существует нуль;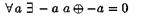 существует обратный элемент;
существует обратный элемент; сложение коммутативно
сложение коммутативно умножение ассоциативно
умножение ассоциативно
 умножение коммутативно.
умножение коммутативно. существует единица
существует единица такими что:
такими что: сложение ассоциативно;
сложение ассоциативно; существует нуль;
существует нуль; существует обратный элемент по сложению;
существует обратный элемент по сложению; сложение коммутативно
сложение коммутативно умножение ассоциативно;
умножение ассоциативно;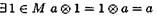 существует единица;
существует единица; существует обратный элемент по умножению;
существует обратный элемент по умножению; умножение коммутативно
умножение коммутативно умножение дистрибутивно относительно сложения.
умножение дистрибутивно относительно сложения. линейных уравнений с
линейных уравнений с  неизвестными (или, кратко, линейная система) имеет следующий вид:
неизвестными (или, кратко, линейная система) имеет следующий вид:
 обозначены неизвестные, подлежащие определению (число их n не предполагается обязательно равным числу уравнений m); величины
обозначены неизвестные, подлежащие определению (число их n не предполагается обязательно равным числу уравнений m); величины  называемые коэффициентами системы, и величины
называемые коэффициентами системы, и величины  называемые свободными членами, предполагаются известными.
называемые свободными членами, предполагаются известными. равны нулю.
равны нулю. отличен от нуля, то система (3.1) называется неоднородной.
отличен от нуля, то система (3.1) называется неоднородной. чисел
чисел 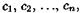 которая при подстановке в систему (3.1) на место неизвестных
которая при подстановке в систему (3.1) на место неизвестных 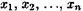 обращает все уравнения этой системы в тождества.
обращает все уравнения этой системы в тождества.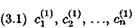 и
и называются различными, если нарушается хотя бы одно из равенств
называются различными, если нарушается хотя бы одно из равенств
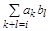 , i=0,1, …, n+s.
, i=0,1, …, n+s.

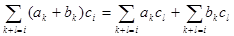
 обратима тогда и только тогда, когда
обратима тогда и только тогда, когда  то есть определитель
то есть определитель  взаимно прост с
взаимно прост с 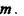

 основной матрицы
основной матрицы
 такие, что при подстановке этих чисел в систему (3.10) все уравнения этой системы обращаются в тождества. Тогда, умножая тождества (3.10) соответственно на алгебраические дополнения
такие, что при подстановке этих чисел в систему (3.10) все уравнения этой системы обращаются в тождества. Тогда, умножая тождества (3.10) соответственно на алгебраические дополнения  элементов
элементов  столбца определителя
столбца определителя  матрицы (3.11) и складывая затем получающиеся при этом тождества, мы получим (для любого номера
матрицы (3.11) и складывая затем получающиеся при этом тождества, мы получим (для любого номера  равного
равного 

 го столбца на соответствующие алгебраические дополнения элементов
го столбца на соответствующие алгебраические дополнения элементов  столбца равна нулю при
столбца равна нулю при 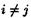 и равна определителю
и равна определителю  матрицы (3.11) при
матрицы (3.11) при  мы получим из последнего равенства
мы получим из последнего равенства
 (или, более кратко, символом
(или, более кратко, символом  ) определитель, получающийся из определителя
) определитель, получающийся из определителя  основной матрицы (3.11) заменой его
основной матрицы (3.11) заменой его  столбца столбцом из свободных членов
столбца столбцом из свободных членов  (с сохранением без изменения всех остальных столбцов
(с сохранением без изменения всех остальных столбцов 
 9), и это равенство принимает вид
9), и это равенство принимает вид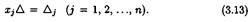
 матрицы (3.11) отличен от нуля, равенства (3.13) эквивалентны соотношениям
матрицы (3.11) отличен от нуля, равенства (3.13) эквивалентны соотношениям
 системы (3.10)
системы (3.10) основной матрицы (3.11), отличным от нуля, существует, то это решение однозначно определяется формулами (3.14).
основной матрицы (3.11), отличным от нуля, существует, то это решение однозначно определяется формулами (3.14).
 ранг основной матрицы равен
ранг основной матрицы равен  а ранг содержащей п строк расширенной матрицы (3.15) больше числа п быть не может и потому равен рангу основной матрицы. Тем самым полностью доказано.
а ранг содержащей п строк расширенной матрицы (3.15) больше числа п быть не может и потому равен рангу основной матрицы. Тем самым полностью доказано. 4.11, п. 2, заключаем, что после удаления из D вершин, содержащихся в D1, имеем орграф D, подграфами которого являются D2,..., Dp, а следовательно, D2,..., Dp являются компонентам^ сильной связности орграфа D. Кроме того, в силу утверждения 4.11, пп. 1, 2, получаем, что объединение множеств вершин орграфов D2,..., Dp дает множество вершин орграфа D, а значит, D2,..., Dp — все компоненты сильной связности орграфа D.
4.11, п. 2, заключаем, что после удаления из D вершин, содержащихся в D1, имеем орграф D, подграфами которого являются D2,..., Dp, а следовательно, D2,..., Dp являются компонентам^ сильной связности орграфа D. Кроме того, в силу утверждения 4.11, пп. 1, 2, получаем, что объединение множеств вершин орграфов D2,..., Dp дает множество вершин орграфа D, а значит, D2,..., Dp — все компоненты сильной связности орграфа D.


