
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аксиоматическое построение теории вероятности.
Введем поле J элементарных событий, т.е. множество событий для к-х определены вероятности. Аксиомы: 1) любому 2) P( 3) Аксиома сложения вероятностей: Вероятность объединения несовместных событий равна сумме их вероятностей. Объединением нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий. Теорема сложения вероятностей. Вероятность появления 1 из 2 несовместных событий равна сумме вероятностей этих событий. P(A+B)=P(A)+P(B);m P(A+B)= Вероятность появления одного из нескольких попарно-несовместных событий равна сумме вероятностей этих событий. P(A Сумма вероятностей A События называются полной группой if Условная вероятность. Вероятность наступления события А, зависящего от наступления события B называется условной вероятностью - P(A|B) = Теорема умножения вероятностей. Произведение событий. (A*B) – совместное появление этих событий. Вероятность совместного появления 2 событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную, предположив, что первое событие уже наступило. P(A*B)=P(A)*P (B|A) = P(B)*P(A|B). Для независимых событий P(A*B)=P(A)*P(B). Вероятность появления нескольких событий равна произведению вероятности одного из них на условную вероятность всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли. P(A
Случайная величина. Законы распределения случайной величины. Математическое ожидание и дисперсия случайной величины: определение, свойства. Вычисление математических ожиданий и дисперсий распределений: биноминального, Пуассона, нормального.
Случайной называется величина, которая в результате опыта может принять то или иное значение (только одно), причем до опыта неизвестно, какое именно. Пространство её значений – вероятностное пространство С.В(случайной величины). Существуют 3 типа С.В.: дискретные, непрерывные, непрерывно-дискретные. Дискретной случайной величиной называется такая величина, число возможных значений которой либо конечное, либо бесконечное (счетное множество). Непрерывной - возможные значения к-й непрерывно заполняют некоторый интервал на числовой оси. Непрерывно-дискретная – С.В, значения к-й непрерывно заполняют отдельные интервалы на числовой оси.
Так же С.В. могут быть классифицированы: a)скалярные(X), векторные(X1,X2,…,Xn). б)действительные, комплексные.
|
|||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 285; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.255.94 (0.004 с.) |
 -пространство элементарных событий. J
-пространство элементарных событий. J 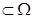 .
.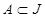 соответствует некоторое неотрицательное число P(A) (вероятность этого события), причем P(A) может быть - 0<=P(A)<=1;
соответствует некоторое неотрицательное число P(A) (вероятность этого события), причем P(A) может быть - 0<=P(A)<=1;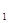 -A, m
-A, m 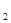 -B. m
-B. m 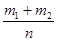 =
= 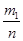 +
+  =P(A)+P(B).(из классического определения вероятности)
=P(A)+P(B).(из классического определения вероятности) )=P(A
)=P(A 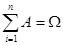 .
.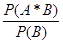 (P(B)
(P(B) 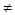 0). Если события независимы (P(A|B)=P(A), P(B|A)=P(B)), то их вероятности безусловные.
0). Если события независимы (P(A|B)=P(A), P(B|A)=P(B)), то их вероятности безусловные. |A1)+…+P (A
|A1)+…+P (A 


