

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Санкционированное получение прав доступа.
Содержание книги
- Если функция непрерывна на отрезке, то она ограничена на нем.
- Параметры и радиус сходимости
- Определение интеграла по Риману
- Аксиоматическое построение теории вероятности.
- Законы больших чисел и предельные теоремы
- Многочлены. Кольцо многочленов над кольцом с единицей. Делимость многочленов, теорема о делении с остатком. Значение и корень многочлена. Теорема безу.
- Теорема. Если натуральные числа а, т взаимно просты, то
- Выделение компонент связности в неориентированном графе
- Алгоритмы поиска в последовательно организованных файлах. Бинарный и интерполяционный поиск. Поиск в файлах, упорядоченных по вероятности. Самоорганизующиеся файлы. Оценки трудоемкости.
- Модель системы безопасности hru. Основные положения Модели. Теорема об алгоритмической неразрешимости проблемы безопасности в произвольной системе.
- Санкционированное получение прав доступа.
- Модель белла-лападулы как основа построения систем мандатного разграничения доступа. Основные положения Модели. Базовая теорема безопасности (BST).
- Проблемы использования Модели бл
- Основная теорема безопасности Белла-ЛаПадулы
- Группа В. Мандатное управление доступом.
- Общая характеристика операционных систем (ОС). Назначение и возможности систем семейств UNIX, Windows.
- Основные механизмы безопасности средств и методы аутентификации в ОС, Модели разграничения доступа, организация и использование средств аудита.
- Методы и средства обеспечения целостности информации в операционных системах семейства Windows NT и Linux.
- Модель разграничения доступа.
- Вредоносное программное обеспечение. Классификация, принципы работы, способы выявления и противодействия.
- Локальные вычислительные сети IEEE 802.3. Методы и средства обеспечения безопасности в проводных сетях.
- Беспроводные локальные сети IEEE 802.11. Методы и средства обеспечения безопасности в беспроводных сетях.
- Виртуальные лвс. Типы VLAN. Стандарт ieee 802. 1q. Формат маркированного кадра Ethernet ieee 802. 1p/q. Правила продвижения пакетов VLAN 802. 1q.
- Межсетевые экраны. Классификация межсетевых экранов. Типовое размещение межсетевого экрана в лвс. Архитектура межсетевых экранов. Политика межсетевых экранов. Понятие dmz. Трансляция ip-адресов.
- Системы обнаружения атак. Классификация систем обнаружения атак. Типовая архитектура систем обнаружения атак. Методы обнаружения информационных атак в системах обнаружения атак.
- Языки запросов. Языки описания данных. Языки манипулирования данными. Особенности языковых средств управления и обеспечения безопасности данных в реляционных СУБД.
- Транзакции. Свойства acid транзакций. Управление восстановлением. Алгоритм aries. Двухфазная фиксация.
- Транзакции. Свойства ACID транзакций. Управление параллельностью. Блокировки. Строгий протокол двухфазной блокировки.
- Технологии удалённого доступа и системы баз данных, тиражирование и синхронизация в распределённых системах баз данных.
- Технические каналы утечки информации, классификация и характеристика
- Оптические каналы утечки информации. Способы и средства противодействия наблюдению в оптическом диапазоне.
- Канал утечки информации за счет пэмин
- Каналы утечки акустической информации.
- Материально-вещественные каналы утечки информации.
- Задачи и принципы инженерно-технической защиты информации.
- Способы и средства инженерной защиты и технической охраны объектов.
- Методика оценки возможности утечки информации по оптическому каналу
- Методика оценки возможности утечки информации по акустическому каналу
- Методика оценки возможности утечки информации по радиоэлектронному каналу
- Оценка эффективности защиты акустической (речевой) информации от утечки по техническим каналам
- Оценка защищенности информации от утечки за счет пэмин
- Способы и средства информационного скрытия речевой информации от подслушивания. Энергетическое скрытие акустического сигнала.
- Основные методы защиты информации техническими средствами.
- Системы шифрования с открытыми ключами: RSA, системы Эль-Гамаля, системы на основе «проблемы рюкзака».
- Формирование цифровой подписи
- Ключевые функции хеширования (называют кодами аутентификации сообщений)
- Объекты правового регулирования при создании и эксплуатации системы информационной безопасности
- Система международных и российских правовых стандартов. Стандарт BS7799
- Значение и отличительные признаки методик служебного расследования фактов нарушения информационной безопасности от расследования других правонарушений
- Инструкция информационной безопасности для рабочего места
Данный способ характеризуется тем, что при передаче прав доступа не накладываются ограничения на кооперацию субъектов системы, участвующих в этом процессе.
Пусть х, уÎО - различные объекты графа доступа G0=(S0,O0,E0), aÍR. Определим предикат "возможен доступ" (a,х,у, G0), который будет истинным тогда и только тогда, когда существуют графы G1=(S1,O1,E1),.... Gn=(Sn,On,En), такие, что:
G0├ op1 G1├ op2…├ opN Gn и (x,y,a)Î En.
Определение 1. Говорят, что вершины графа доступов являются tg-связными или что они соединены tg-путем, если (без учета направления дуг) в графе между ними существует такой путь, что каждая дуга этого пути помечена t или g. Будем говорить, что вершины непосредственно tg-связны, если tg-путъ между ними состоит из единственной дуги.
Теорема 1. Пусть G0=(S0,O0,E0) – граф доступов, содержащий только вершины-субъекты. Тогда предикат "возможен доступ" (a,х,у,G0) истинен тогда и только тогда, когда выполняются следующие условия:
- Существуют субъекты sl.... sm, такие, что (si,y,gi,)ÎE0 для i=1,...,m и a = g1È…È gm.
- Субъект х соединен в графе G0 tg-путем с каждым субъектом si, для i=1,...,m.
Для определения истинности предиката "возможен доступ" в произвольном графе необходимо ввести ряд дополнительных понятий.
Определение 2. Островом в произвольном графе доступов G0 называется его максимальный tg-связный подграф, состоящий только из вершин субъектов.
Определение 3. Мостом в графе доступов G0 называется tg-путь, концами которого являются вершины-субъекты; при этом словарная запись tg-пути должна иметь вид 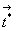 , , 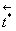 , ,  , ,  , где символ * означает многократное (в том числе нулевое) повторение. , где символ * означает многократное (в том числе нулевое) повторение.
Определение 4. Начальным пролетом моста в графе доступов G0 называется tg-путь, началом которого является вершина-субъект; при этом словарная запись tg-пути должна иметь вид 
Определение 5. Конечным пролетом моста в графе доступов G0 называется tg-путь, началом которого является вершина-субъект; при этом словарная запись tg-пути должна иметь вид 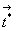 . .
Теорема 2. Пусть G0=(S0,O0,E0) - произвольный граф доступов. Предикат "возможен доступ"(a,х,у, G0) истинен тогда и только тогда, когда выполняются условия:
- Существуют объекты s1,...,sm, такие, что (si,y,gi)ÎE0, i=1,...,m, и a = g1È…È gm.
- Существуют вершины-субъекты x1,...,xm и s1,...,sm, такие, что:
· х=хi или хi, соединен с х начальным пролетом моста для i=1,...,m;
· si=si или si соединен с а конечным пролетом моста для i=1,.... m.
- Для каждой пары (хi, si), i=1,...,m, существуют острова li,1… li,ui, ui³1, такие, что хiÎ li,1, siÎ li,ui и мосты между островами li,j и li,j+1,ui>j³1.
Похищение прав доступа
Способ передачи прав доступа предполагает идеальное сотрудничество субъектов В случае похищения прав доступа предполагается, что передача прав доступа объекту осуществляется без содействия субъекта, изначально обладавшего передаваемыми правами Пусть х,у  О-различные объекты графа доступа Go = (So,O0,Eo), a О-различные объекты графа доступа Go = (So,O0,Eo), a 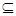 R Определим предикат "возможно похищение" (a,x,y,Go), который будет истинным тогда и только тогда, когда (x,y,a) R Определим предикат "возможно похищение" (a,x,y,Go), который будет истинным тогда и только тогда, когда (x,y,a)  Eo и существуют графы Eo и существуют графы  = ( = ( ), ),  , такие, что , такие, что
 и (x,y,a) и (x,y,a)   , при этом, если , при этом, если  (s,y,a) (s,y,a)  Eo, то Eo, то  =0,1,, N выполняется opK =0,1,, N выполняется opK 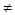 granf(a,s,z,y), К=1, N. granf(a,s,z,y), К=1, N.
Теорема 2. Пусть Go = (So, Oo, Eo)- произвольный граф доступов Предикат "возможно похищение" (a,x,y,Go) истинен тогда и только тогда, когда выполняются условия:
- (х,у,а)  Ео Ео
- Существуют объекты  ,…,sm, такие, что (s,y, ,…,sm, такие, что (s,y, 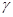 ,) ,)  Eo для i=1,… ,т и a = Eo для i=1,… ,т и a = 
- Являются истинными предикаты "возможен доступ" (t,x, s,Go) для i =1,… ,m
Расширенная модель Take-Grant и ее применение для анализа информационных потоков в АС.
В расширенной модели Take-Grant рассматриваются пути и стоимости возникновения информационных потоков в системах с дискреционным разграничением доступа
В классической модели Take-Grant по существу рассматриваются два права доступа t и g, а также четыре правила (правила де-юре) преобразования графа доступов take, grant, create, remove В расширенной модели дополнительно рассматриваются два права доступа на чтение r (read) и на запись w (write), а также шесть правил (правила де-факто) преобразования графа доступов post, spy, find, pass и два правила без названия.
Правила де-факто служат для поиска путей возникновения возможных информационных потоков в системе. Эти правила являются следствием уже имеющихся у объектов системы прав доступа и могут стать причиной возникновения информационного потока от одного объекта к другому без их непосредственного взаимодействия.
В результате применения к графу доступов правил де-факто в него добавляются мнимые дуги, помечаемые r или w и изображаемые пунктиром. Вместе с дугами графа, соответствующими правам доступа r и w (реальными дугами), мнимые дуги указывают на направления информационных каналов в системе.

Правила де-факто (везде вместо реальных дуг могут быть мнимые дуги)
Важно отметить, что к мнимым дугам нельзя применять правила де-юре преобразования графа доступов. Информационные каналы нельзя брать или передавать другим объектам системы.
|