Если функция непрерывна на отрезке, то она ограничена на нем.
Содержание книги
- Если функция непрерывна на отрезке, то она ограничена на нем.
- Параметры и радиус сходимости
- Определение интеграла по Риману
- Аксиоматическое построение теории вероятности.
- Законы больших чисел и предельные теоремы
- Многочлены. Кольцо многочленов над кольцом с единицей. Делимость многочленов, теорема о делении с остатком. Значение и корень многочлена. Теорема безу.
- Теорема. Если натуральные числа а, т взаимно просты, то
- Выделение компонент связности в неориентированном графе
- Алгоритмы поиска в последовательно организованных файлах. Бинарный и интерполяционный поиск. Поиск в файлах, упорядоченных по вероятности. Самоорганизующиеся файлы. Оценки трудоемкости.
- Модель системы безопасности hru. Основные положения Модели. Теорема об алгоритмической неразрешимости проблемы безопасности в произвольной системе.
- Санкционированное получение прав доступа.
- Модель белла-лападулы как основа построения систем мандатного разграничения доступа. Основные положения Модели. Базовая теорема безопасности (BST).
- Проблемы использования Модели бл
- Основная теорема безопасности Белла-ЛаПадулы
- Группа В. Мандатное управление доступом.
- Общая характеристика операционных систем (ОС). Назначение и возможности систем семейств UNIX, Windows.
- Основные механизмы безопасности средств и методы аутентификации в ОС, Модели разграничения доступа, организация и использование средств аудита.
- Методы и средства обеспечения целостности информации в операционных системах семейства Windows NT и Linux.
- Модель разграничения доступа.
- Вредоносное программное обеспечение. Классификация, принципы работы, способы выявления и противодействия.
- Локальные вычислительные сети IEEE 802.3. Методы и средства обеспечения безопасности в проводных сетях.
- Беспроводные локальные сети IEEE 802.11. Методы и средства обеспечения безопасности в беспроводных сетях.
- Виртуальные лвс. Типы VLAN. Стандарт ieee 802. 1q. Формат маркированного кадра Ethernet ieee 802. 1p/q. Правила продвижения пакетов VLAN 802. 1q.
- Межсетевые экраны. Классификация межсетевых экранов. Типовое размещение межсетевого экрана в лвс. Архитектура межсетевых экранов. Политика межсетевых экранов. Понятие dmz. Трансляция ip-адресов.
- Системы обнаружения атак. Классификация систем обнаружения атак. Типовая архитектура систем обнаружения атак. Методы обнаружения информационных атак в системах обнаружения атак.
- Языки запросов. Языки описания данных. Языки манипулирования данными. Особенности языковых средств управления и обеспечения безопасности данных в реляционных СУБД.
- Транзакции. Свойства acid транзакций. Управление восстановлением. Алгоритм aries. Двухфазная фиксация.
- Транзакции. Свойства ACID транзакций. Управление параллельностью. Блокировки. Строгий протокол двухфазной блокировки.
- Технологии удалённого доступа и системы баз данных, тиражирование и синхронизация в распределённых системах баз данных.
- Технические каналы утечки информации, классификация и характеристика
- Оптические каналы утечки информации. Способы и средства противодействия наблюдению в оптическом диапазоне.
- Канал утечки информации за счет пэмин
- Каналы утечки акустической информации.
- Материально-вещественные каналы утечки информации.
- Задачи и принципы инженерно-технической защиты информации.
- Способы и средства инженерной защиты и технической охраны объектов.
- Методика оценки возможности утечки информации по оптическому каналу
- Методика оценки возможности утечки информации по акустическому каналу
- Методика оценки возможности утечки информации по радиоэлектронному каналу
- Оценка эффективности защиты акустической (речевой) информации от утечки по техническим каналам
- Оценка защищенности информации от утечки за счет пэмин
- Способы и средства информационного скрытия речевой информации от подслушивания. Энергетическое скрытие акустического сигнала.
- Основные методы защиты информации техническими средствами.
- Системы шифрования с открытыми ключами: RSA, системы Эль-Гамаля, системы на основе «проблемы рюкзака».
- Формирование цифровой подписи
- Ключевые функции хеширования (называют кодами аутентификации сообщений)
- Объекты правового регулирования при создании и эксплуатации системы информационной безопасности
- Система международных и российских правовых стандартов. Стандарт BS7799
- Значение и отличительные признаки методик служебного расследования фактов нарушения информационной безопасности от расследования других правонарушений
- Инструкция информационной безопасности для рабочего места
2. Теорема Вейерштрасса:
Пусть f(x) непрерывна на отрезке [a;b]. Тогда  

Следствие: если функция непрерывна на отрезке, то она достигает наибольшего и наименьшего значения на нем.
3. Теорема Больцано-Коши:
Пусть f(x) непрерывна на отрезке [a;b], f(a) = A, f(b) = B, A 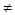 B. B.
Тогда  , A< , A<  <B <B   [a; b]: [a; b]:  . .
Следствие: если функция непрерывна на отрезке, то она принимает все значения на нем.
Прим.: теорема не утверждает, что точка  - единственная. - единственная.
Непрерывность многочленной и рациональной функции:
Т.к. произведение непрерывных функций есть функция непрерывная, отсюда следует непрерывность любого одночленного выражения ax  = a* = a*  (if F(x)=x непрерывная функция). (if F(x)=x непрерывная функция).
Непрерывность многочлена (целой рациональной функции) a  x x  + a + a 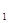 x x  + … + a + … + a  x + a x + a  следует из непрерывности суммы непрерывных функций. В этих случаях непрерывность имеет место во всем промежутке (- следует из непрерывности суммы непрерывных функций. В этих случаях непрерывность имеет место во всем промежутке (-  ; + ; +  ).(Сумма непрерывных функций есть непрерывная функция) ).(Сумма непрерывных функций есть непрерывная функция)
Частное двух многочленов (дробная рациональная функция)  
также будет непрерывно при каждом значении x, кроме тех, которые обращают знаменатель в 0.
Терема о среднем для действительных функций одного действительного переменного. Теорема Ферма; теорема Ролля; теорема Лагранжа. Примеры показывающие существенность каждого условия в теореме Роля; геометрическая интерпретация.
Теорема о среднем – совокупность: Т. Ферма, Т. Роля, Т. Коши, Т. Лагранжа.
Теорема Ферма:
Пусть функция  определена и непрерывна на промежутке [a;b] и в некоторой точке определена и непрерывна на промежутке [a;b] и в некоторой точке 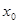 этого промежутка достигает своего наибольшего и наименьшего значения, если в этой точке этого промежутка достигает своего наибольшего и наименьшего значения, если в этой точке  , то , то 
Доказательство:
Пусть, для определенности, в точке 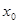 функция функция 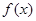 достигает своего наибольшего. По условию теоремы эта точка внутренняя, т.е. a<x<b, и поэтому к этой точке можно подойти и справа и слева. достигает своего наибольшего. По условию теоремы эта точка внутренняя, т.е. a<x<b, и поэтому к этой точке можно подойти и справа и слева.
Пусть мы подходим к точке 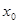 слева. Тогда слева. Тогда  ,т.к. ,т.к.  -наибольшее значение. -наибольшее значение.
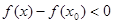 , ,  (т.к. подходим слева) => (т.к. подходим слева) => 

Делая предельный переход 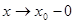 получим получим  (1) (1)
Пусть мы подходим к точке 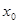 справа. Тогда справа. Тогда  ,т.к. ,т.к.  -наибольшее значение. -наибольшее значение.
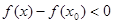 , ,  (т.к. подходим справа) => (т.к. подходим справа) => 

Делая предельный переход  получим получим 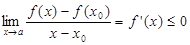 (2) (2)
Сопоставляя соотношения (1) и (2), приходим к заключению, что 
Аналогично для наименьшего значения.
Теорема Ролля:
Пусть:
1) функция f(x) определена и непрерывна на замкнутом промежутке [a; b];
2)  ; ;
3) на концах промежутка функция принимает равные значения 
Тогда  : : 
Доказательство: f(x) непрерывна в замкнутом промежутке [a; b], поэтому
 – по т.Вейрштрасса – по т.Вейрштрасса
 x x  [a; b] m <= f(x) <= M. [a; b] m <= f(x) <= M.
Рассмотрим 2 случая:
1) M=m. Тогда f(x) в промежутке [a; b] сохраняет постоянное значение. Производная const равна 0.
2)  (M>m). (M>m).
Оба эти значения функцией достигаются, но, т.к. f(a) = f(b), то они не могут оба достигаться на концах промежутка и хоть одно из них достигается в некоторой точке между a и b (Если, к примеру, 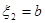 , тогда , тогда 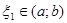 , т.е. не может быть равно а). Производная в этой точке обращается в 0 (либо , т.е. не может быть равно а). Производная в этой точке обращается в 0 (либо  , либо , либо  - из т.Ферма). Теорема доказана. - из т.Ферма). Теорема доказана.
Замечание: теорема Ролля не утверждает, что такая точка одна.
На геометрическом языке теорема Роля означает следующее: если крайние кординаты кривой y=f(x) равны, то на кривой найдется точка, где касательная параллельна оси x.

Примеры показывающие существенность условий - в доказательстве (без всех условий теорема не доказуема).
Теорема Лагранжа. Пусть:
1) f(x) определена и непрерывна на замкнутом промежутке [a; b],
2) f(x) дифференцируема на (a; b).
Тогда 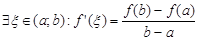
Доказательство: Введем вспомогательную функцию F(x), определив ее в промежутке [a; b] равенством: 
Эта функция непрерывна на [a; b], т.к. представляет собой разность между непрерывной функцией f(x) и линейной функцией. В промежутке (a; b) она имеет определенную конечную производную, равную
 . .
Подстановкой можно убедиться, что F(a)=F(b)=0, т. е. F(x) принимает равные значения на концах промежутка. Следовательно, по теореме Ролля, на интервале (a; b) существует 
 , т. е , т. е  Теорема доказана. Теорема доказана.
|