
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметры и радиус сходимости
Сходимость: пусть есть ряда1+а2+…+аn+… Его частичные суммы: S1=a1, S2=a1+a2 , …,Sn= a1 +…. + an . Ряд сходится if Из теоремы Абеля можно сделать заключение о характере области сходимости степенного ряда. Точка z=0 всегда лежит в области сходимости ряда (1). Если область сходимости отлична от одной точки z=0 и от всей плоскости (z), то существует круг радиуса R, называемый кругом сходимости степенного ряда(1), в каждой точке которого ряд (1) сходится абсолютно, а вне точек круга расходится.
Для определения радиуса круга сходимости используется либо признак Даламбера, либо признак Коши. Для каждого фиксированного z рассмотрим числовой ряд Т.о., для определения радиуса круга сходимости степенного ряда получаем формулу Если же к ряду (3) применим признак Коши то получим равенство
Радиус сходимости степенного ряда - Rcx= Критерий равномерной сходимости. Для того, чтобы функциональный ряд(в частности степенной ряд) сходился равномерно в области D, необходимо и достаточно, чтобы
Абсолютная сходимость: ряд а1+а2+…+аn+… сходится абсолютно, если сходится ряд |а1 |+|а2 |+…+|аn |+… Непрерывность суммы Свойство степенных рядов. Сумма степенного ряда есть функция, непрерывная на интервале сходимости ряда. S(z) = z0 + a1z + a2z2 + … + anzn + … Причём, в том конце интервала, где степенной ряд сходится, его сумма S(x) остаётся односторонне непрерывной. Почленная дифференцируемость Теорема1:. C тепенной ряд внутри интервала сходимости (|z|<R) имеет сумму S(x), к-я дифференцируема сколь угодно много раз. Степенной ряд можно почленно дифференцировать любое число раз, причем радиус круга сходимости продифференцированных рядов также равен R. S(x)= с0 + с1(z – z0) + с2(z – z0)2 + … + сn(z – z0)n + … S’(x)= с1 + с2 *2*(z – z0) + … + сn *n*(z – z0)n-1 + … Ряд Тейлора
Имеем степенной ряд
Первообразная и неопределённый интеграл. Определение первообразной. Определение неопределённого интеграла, его свойства. Определение интеграла по Риману. Необходимые и достаточные свойства интегрируемости. Формула Ньютона-Лейбница. Пусть определены функции f(x) и F(x). F(x) – первообразная f(x), если F’(x) = f(x). F(x) + c – тоже первообразная f(x). Неопределенный интеграл: Свойства неопределенного интеграла: 1) 2) d 3) 4)
|
|||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.8.34 (0.006 с.) |
 , где S конечно.
, где S конечно.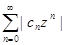 (3) и применим к нему признак Даламбера. Именно: если существует предел
(3) и применим к нему признак Даламбера. Именно: если существует предел  (4), то ряд (3) сходится, если
(4), то ряд (3) сходится, если  и расходится, если
и расходится, если 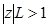 . Отсюда заключаем, что если выполнено соотношение
. Отсюда заключаем, что если выполнено соотношение  , то ряд (3) сходится абсолютно, а если имеет место неравенство
, то ряд (3) сходится абсолютно, а если имеет место неравенство  , то ряд (1) как и ряд (3), расходится.
, то ряд (1) как и ряд (3), расходится. (5).
(5). из которого заключаем, что ряд (3) сходится, если
из которого заключаем, что ряд (3) сходится, если  , и расходится, если
, и расходится, если  . Т.о., радиус круга сходимости R ряда (1) определяется по формуле
. Т.о., радиус круга сходимости R ряда (1) определяется по формуле 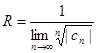 . (6) (формула Коши — Адамара.)
. (6) (формула Коши — Адамара.) =
= 
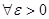 и
и 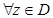
 : при n>N
: при n>N , p =0,1,2,3,…
, p =0,1,2,3,… . Обозначим через f(z) его сумму. Сходится в круге |z -
. Обозначим через f(z) его сумму. Сходится в круге |z - 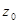 |<R.
|<R. называется рядом Тейлора функции f(z) по степеням (z-
называется рядом Тейлора функции f(z) по степеням (z-  - эти выражения называются коэффициентами Тейлора функции f(z) в точке
- эти выражения называются коэффициентами Тейлора функции f(z) в точке 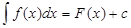 - множество всех первообразных f(x).
- множество всех первообразных f(x).

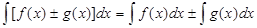
 , где с – const
, где с – const


