
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многочлены. Кольцо многочленов над кольцом с единицей. Делимость многочленов, теорема о делении с остатком. Значение и корень многочлена. Теорема безу.
Пусть 1) Структура 2) Структура 3) Операции сложения и умножения связаны законом дистрибутивности: Структура Тогда алгебраическая структура Пусть Суммой многочленов Произведением многочленов Произведением многочлена Суммой элемента Во всех последовательностях в вышеприведенных определениях, так же как и в исходных последовательностях, все коэффициенты, за исключением конечного их числа, равны нулю, и потому эти последовательности принадлежат Используя заданные на Заметим, что ввиду определения произведения многочленов для любых
Поэтому для любых Пользуясь определением произведения многочлена на элемент множества Последнюю запись многочлена При введенных обозначениях многочлен
Алгебра Говорят, что элемент Однако если Говорят, что в кольце При этом многочлены Если старший коэффициент многочлена Если Значением многочлена Данное определение позволяет поставить в соответствие каждому многочлену Очевидно, что значение суммы двух многочленов в любой точке Если Теорема Безу. Остаток от деления справа многочлена
Доказательство. //(хз надо или нет)
Кольца матриц. Матрицы над кольцом и операции над ними. Кольцо квадратных матриц. Определители квадратных матриц над коммутативным кольцом с единицей. Критерий обратимости матрицы над коммутативным кольцом с единицей. Матрицей называется прямоугольная таблица чисел, состоящая из m строк и n столбцов. Числа m, n наз. порядком матрицы. Если m=n, матрица называется квадратной. Множество квадратных матриц порядка n относительно операции сложения и умножения матриц есть кольцо с единицей Е – единичной матрицей, при n>1 оно некоммутативно. Операции над матрицами:
Матрицу А можно умножить не на всякую матрицу В: необходимо, чтобы число столбцов матрицы А было = числу строк матрицы В. Для того чтобы оба произведения А *B и B*A были определены необходимо и достаточно, чтобы обе матрицы A и В были квадр матрицами одного и того же порядка.
Определители Кольцо коммутативно если а*b=b*a – умножение коммутативно Коммутативное Кольцо с единицей если существует 1ЄМ а*1=1*а=а
Если порядок матрицы равен единице, то эта матрица состоит из одного элемента
Перейдем теперь к выяснению понятия определителя любого порядка п, где Договоримся называть минором любого элемента Определителем порядка п,, назовем число, равное Итак, по определению Формула (1.12) представляет собой правило составления определителя порядка п по элементам первой строки соответствующей ему матрицы и по минорам К – кольцо с единицей. Элемент а называется обратимым, if существует такой элемент а-1, для которого аа-1=а-1а=1.
Теорема. Для того, чтобы для матрицы А существовали левая и правая обратные матрицы, необходимо и достаточно, чтобы определитель det А матрицы А был отличен от нуля. Замечание 1. Квадратную матрицу А, определитель det А которой отличен от нуля, принято называть невырожденной.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 685; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.154.103 (0.021 с.) |
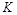 - непустое множество, на котором заданы две бинарные операции: сложение и умножение, удовлетворяющие следующим условиям:
- непустое множество, на котором заданы две бинарные операции: сложение и умножение, удовлетворяющие следующим условиям: есть абелева группа, то есть сложение коммутативно и ассоциативно, существует нейтральный элемент (ноль) по сложению и для любого
есть абелева группа, то есть сложение коммутативно и ассоциативно, существует нейтральный элемент (ноль) по сложению и для любого 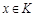 существует единственный противоположный к нему элемент.
существует единственный противоположный к нему элемент. есть полугруппа, то есть умножение ассоциативно;
есть полугруппа, то есть умножение ассоциативно; и
и 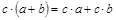 для любых
для любых  .
. называется кольцом.
называется кольцом.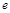 . Многочленом над
. Многочленом над  элементов
элементов  , в которой все
, в которой все  , за исключением конечного их числа, равны нулю. Элементы
, за исключением конечного их числа, равны нулю. Элементы  назовем коэффициентами многочлена. Многочлен
назовем коэффициентами многочлена. Многочлен  назовем нулевым. Обозначим через
назовем нулевым. Обозначим через  множество всех таких последовательностей. Номер последнего ненулевого члена последовательности
множество всех таких последовательностей. Номер последнего ненулевого члена последовательности  .
. называют последовательность
называют последовательность  , в которой для всех
, в которой для всех 
 .
. , в которой
, в которой  для всех
для всех  на элемент
на элемент  слева или справа называют, соответственно, последовательность
слева или справа называют, соответственно, последовательность 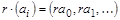 или
или  .
. .
. ,
,  для
для  выполняются равенства:
выполняются равенства:
 верны равенства
верны равенства  и для
и для  символ
символ  обозначает ни что иное, как
обозначает ни что иное, как  -ю степень элемента
-ю степень элемента 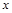 :
:  .
. и
и  , и поэтому любой многочлен
, и поэтому любой многочлен  может быть записан в виде суммы:
может быть записан в виде суммы: 
 .
. называют его коэффициентами. Говорят, что
называют его коэффициентами. Говорят, что 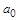 - его свободный член. Множество
- его свободный член. Множество  .
. многочленов над кольцом
многочленов над кольцом 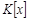 коммутативно тогда и только тогда, когда кольцо
коммутативно тогда и только тогда, когда кольцо  кольца
кольца  делится на элемент
делится на элемент  слева (справа), если в
слева (справа), если в  .
. - кольцо многочленов над кольцом
- кольцо многочленов над кольцом  справа с остатком, если существуют многочлены
справа с остатком, если существуют многочлены  со свойствами
со свойствами  ,
,  . //(deg – обозначение степени многочлена)
. //(deg – обозначение степени многочлена)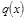 и
и  называют, соответственно, неполным правым частным и правым остатком от деления
называют, соответственно, неполным правым частным и правым остатком от деления  обратим в кольце
обратим в кольце  можно разделить справа (слева) с остатком на
можно разделить справа (слева) с остатком на  - поле и
- поле и  , то любой многочлен
, то любой многочлен  можно разделить с остатком на
можно разделить с остатком на  называют элемент кольца
называют элемент кольца  . Говорят, что
. Говорят, что  .
.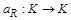 , определяемую условием
, определяемую условием  .
. ,
,  и элемент
и элемент  перестановочен со всеми коэффициентами правого множителя
перестановочен со всеми коэффициентами правого множителя  . При сформулированном условии верны равенства
. При сформулированном условии верны равенства  .
. равен
равен  . В частности, элемент
. В частности, элемент .
. :
:  ,
,  . Тогда
. Тогда  , где
, где 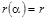 . Так как для многочлена
. Так как для многочлена  верно равенство
верно равенство  , то
, то 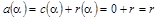 . В частности, равенство
. В частности, равенство  , а последнее эквивалентно тому, что
, а последнее эквивалентно тому, что  Сложение матриц обладает переместительным свойством: А + В = Б + А; и сочетательным свойством: (А + В) + С = А + (В + С).
Сложение матриц обладает переместительным свойством: А + В = Б + А; и сочетательным свойством: (А + В) + С = А + (В + С).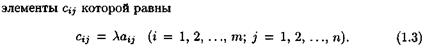

 Для обозначения произведения матрицы на число используется запись
Для обозначения произведения матрицы на число используется запись  или
или  . Операция составления произведения матрицы на число называется умножением матрицы на это число. Умножение матрицы на число обладает 1)сочетательным свойством относительно числового множителя:
. Операция составления произведения матрицы на число называется умножением матрицы на это число. Умножение матрицы на число обладает 1)сочетательным свойством относительно числового множителя:  2)распределительным свойством относительно суммы матриц:
2)распределительным свойством относительно суммы матриц:  3)распределительным свойством относительно суммы чисел:
3)распределительным свойством относительно суммы чисел: 

 и определителем первого порядка, соответствующим такой матрице, мы назовем величину этого элемента. Если далее порядок матрицы равен двум, то определителем второго порядка, соответствующим такой матрице, назовем число, равное
и определителем первого порядка, соответствующим такой матрице, мы назовем величину этого элемента. Если далее порядок матрицы равен двум, то определителем второго порядка, соответствующим такой матрице, назовем число, равное  и обозначаемое одним из символов
и обозначаемое одним из символов  . Итак, по определению
. Итак, по определению  (1.10) Формула (1.10) представляет собой правило составления определителя второго порядка по элементам соответствующей ему матрицы.
(1.10) Формула (1.10) представляет собой правило составления определителя второго порядка по элементам соответствующей ему матрицы. Понятие такого определителя мы введем индуктивно, считая, что нами уже введено понятие определителя порядка п — 1, соответствующего произвольной квадратной матрице порядка п — 1.
Понятие такого определителя мы введем индуктивно, считая, что нами уже введено понятие определителя порядка п — 1, соответствующего произвольной квадратной матрице порядка п — 1. матрицы n-го порядка (1.8) определитель порядка п — 1, соответствующий той матрице, которая получается из матрицы (1.8) в результате вычеркивания i-й строки и j-го столбца (той строки и того столбца, на пересечении которых стоит элемент
матрицы n-го порядка (1.8) определитель порядка п — 1, соответствующий той матрице, которая получается из матрицы (1.8) в результате вычеркивания i-й строки и j-го столбца (той строки и того столбца, на пересечении которых стоит элемент  ). Минор элемента
). Минор элемента  будем обозначать символом
будем обозначать символом  . В этом обозначении верхний индекс обозначает номер строки, нижний — номер столбца, а черта над М означает, что указанные строка и столбец вычеркиваются.
. В этом обозначении верхний индекс обозначает номер строки, нижний — номер столбца, а черта над М означает, что указанные строка и столбец вычеркиваются.
 . (1.12)
. (1.12) элементов первой строки, являющимися определителями порядка п — 1.
элементов первой строки, являющимися определителями порядка п — 1.


 Понятие обратной матрицы. Пусть А —квадратная матрица n-го порядка, а Е — единичная квадратная матрица того же порядка Матрица В называется правой обратной по отношению к матрице А, если АВ = Е. Матрица С называется левой обратной по отношению к матрице А, если С А = Е.
Понятие обратной матрицы. Пусть А —квадратная матрица n-го порядка, а Е — единичная квадратная матрица того же порядка Матрица В называется правой обратной по отношению к матрице А, если АВ = Е. Матрица С называется левой обратной по отношению к матрице А, если С А = Е.


