Вопрос 19.1. Условный экстремум.
Похожие статьи вашей тематики
Определение 19.1. Условным минимумом функции n переменных 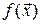 при наличии m условий связи при наличии m условий связи
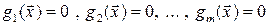 , ,
называется точка  , такая что , такая что
 , ,
и для всех  из некоторой окрестности точки из некоторой окрестности точки  , удовлетворяющих уравнениям связи, выполняется неравенство , удовлетворяющих уравнениям связи, выполняется неравенство  . .
Конец определения.
Определение 19.2. Условным максимумом функции n переменных 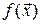 при наличии m условий связи при наличии m условий связи
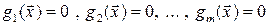
называется точка  , такая что , такая что
 , ,
и для всех  из некоторой окрестности точки из некоторой окрестности точки  , удовлетворяющих уравнениям связи, выполняется неравенство , удовлетворяющих уравнениям связи, выполняется неравенство  . .
Конец определения.
Определение 19.3. Условным экстремумом функции n переменных называется точка условного максимума или локального минимума.
Пример 19.1.  . .
Точкой условного минимума будет  (смотри рис. 1). Действительно из уравнения связи (смотри рис. 1). Действительно из уравнения связи  , или , или 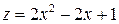 , но , но  . .
Конец примера.
Вопрос 19.2. Функция Лагранжа и множители Лагранжа.
Теорема 19.1. (Необходимые условия существования условного экстремума). Пусть на множестве M непрерывно дифференцируема функция  и и  . Тогда для того, чтобы точка . Тогда для того, чтобы точка  была точкой условного экстремума функции была точкой условного экстремума функции 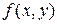 при наличии уравнения связи необходимо, чтобы выполнялись условия при наличии уравнения связи необходимо, чтобы выполнялись условия

Доказательство. Из условия теоремы следует, что уравнение связи определяет неявную функцию 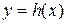 . В точке условного локального экстремума функция . В точке условного локального экстремума функция  имеет безусловный экстремум. Поэтому имеет безусловный экстремум. Поэтому
 . .
Условие  очевидно. Из очевидно. Из  . .
Из последнего уравнения получаем  . Откуда находим . Откуда находим
 . .
Умножим на 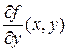 равенство равенство  и заменим и заменим  . Тогда получим . Тогда получим
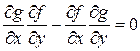 , ,
или
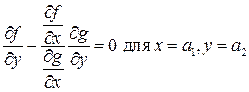 . .
Так как  и и  , то , то  , откуда следует доказательство теоремы. , откуда следует доказательство теоремы.
Конец доказательства.
Замечание 19.1. Если ввести функцию Лагранжа
 , ,
где  - множитель Лагранжа, то необходимые условия существования можно свести к условиям - множитель Лагранжа, то необходимые условия существования можно свести к условиям

Если x и y удовлетворяют уравнению связи 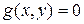 , то функция Лагранжа совпадает с функцией , то функция Лагранжа совпадает с функцией 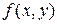 . .
Теорема 19.2. (Достаточные условия существования условного экстремума). Пусть точка  является стационарной точкой функции является стационарной точкой функции 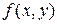 при наличии связи при наличии связи 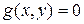 . Если второй дифференциал функции Лагранжа, вычисленный по x и y при условии что . Если второй дифференциал функции Лагранжа, вычисленный по x и y при условии что  , знакопостоянен, то это точка условного локального экстремума, при чем, если , знакопостоянен, то это точка условного локального экстремума, при чем, если  , то это точка условного минимума, в противном случае - точка локального максимума. Если второй дифференциал функции Лагранжа меняет свой знак, то условного экстремума нет. , то это точка условного минимума, в противном случае - точка локального максимума. Если второй дифференциал функции Лагранжа меняет свой знак, то условного экстремума нет.
Теорема приводится без доказательства.
Пример 19.2.  . Найти условный экстремум и определить тип экстремума. . Найти условный экстремум и определить тип экстремума.
Составим функцию Лагранжа  . В точках локального экстремума должны выполняться условия . В точках локального экстремума должны выполняться условия
 . .
откуда получаем систему уравнений

Отсюда получаем:

Вычислим второй дифференциал функции Лагранжа 

С учетом уравнения связи  , получим , получим

В точке  второй дифференциал отрицателен второй дифференциал отрицателен
 . .
Следовательно, это точка условного локального максимума. В точке  второй дифференциал отрицателен второй дифференциал отрицателен
 . .
Следовательно, это точка условного локального минимума.
Конец примера.
|