
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция № 23. Дифференциальные уравнения.
Вопрос 23.1. Уравнения вида Вопрос 23.2. Уравнения вида Вопрос 23.3. Уравнение вида Вопрос 23.4. Уравнения вида Вопрос 23.5. Уравнения вида ЛЕКЦИЯ № 24. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Вопрос 24.1. Метод Пикара (метод последовательных приближений). Вопрос 24.2. Разностные методы дифференциальных уравнений. Метод Эйлера. ЛЕКЦИЯ № 25. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Вопрос 25.1. Метод Рунге-Кутта. Вопрос 25.2. Устойчивость, сходимость разностного метода. Влияние ошибок округления. ЛЕКЦИЯ № 26. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Вопрос 26.1. Линейные дифференциальные уравнения. Основные определения и классификация. Вопрос 26.2. Задача коши для линейного дифференциального уравнения. Теорема существования и единственности. Вопрос 26.3. Общие свойства линейных уравнений. Вопрос 26.4. Линейно независимые и линейно зависимые системы функций. Определитель Вронского. Вопрос 26.5. Уравнение Лиувилля. Формула Лиувилля. ЛЕКЦИЯ № 27. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Вопрос 27.1. Следствия из формулы Лиувилля. Вопрос 27.2. Фундаментальная система решений (ФСР). ЛЕКЦИЯ № 28. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Вопрос 1. Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Фундаментальная система решений. Вопрос 28.2. Метод вариации постоянных коэффициентов. ЛЕКЦИЯ № 29. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Вопрос 29.1. Линейные дифференциальные уравнения с постоянными коэффициентами и со специальной правой частью. ЛЕКЦИЯ № 30. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Вопрос 1. Линейные дифференциальные уравнения старших порядков. Вопрос 30.2. Системы линейных дифференциальных уравнений первого порядка. Список литературы ……………………………………………………….157 ЛЕКЦИЯ № 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. Вопрос 1.1. Первообразная и неопределенный интеграл. Определение 1.1.1. Функция Конец определения. Очевидно, что если Теорема 1.1.1. Если Доказательство. Так как выполняются равенства
Из равенства нулю производной, заключаем, что разность функций принимает постоянное значение, откуда и следует доказываемое утверждение
Конец доказательства. Определение 1.1.2. Неопределенным интегралом от функции
Конец определения. Свойства неопределенного интеграла: 1) 2) Доказательство. Доказательство следует из равенства:
Конец доказательства. 3) Доказательство. Пусть
Поскольку равенство неопределенных интегралов понимается с точностью до константы, то отсюда следует доказываемое соотношение. Конец доказательства. 4) Доказывается аналогично 3-ему свойству. 5) Доказательство. Пусть
где учтено, что Конец доказательства. 6) Доказательство. Пусть
Отсюда получаем
Конец доказательства. Вопрос 1.2. Таблица интегралов. Таблица интегралов играет в высшей математике такую же важную роль, что и таблица производных. Она состоит из наиболее часто встречающихся интегралов от элементарных функций. Эти интегралы получаются с помощью таблицы производных из определения неопределенного интеграла.
1. 2. 3.
4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. Докажем например формулу 2. Вычислим производную от Замечание 1.1. Некоторые интегралы могут быть выражены через другие функции. Например:
где
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 176; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.118.244 (0.01 с.) |
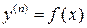 .
. .
. .
. .
.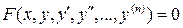 , где
, где  - однородная функция k -го порядка относительно
- однородная функция k -го порядка относительно 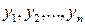 .
.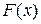 называется первообразной для функции
называется первообразной для функции  на интервале
на интервале 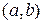 , если
, если 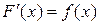 для всех x из интервала
для всех x из интервала 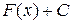 тоже первообразная для
тоже первообразная для 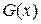 две первообразные для функции
две первообразные для функции  , то, вычитая из первого равенства второе, получим
, то, вычитая из первого равенства второе, получим .
. .
.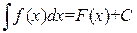 .
.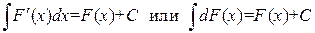 ,
,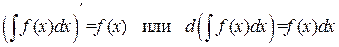 .
.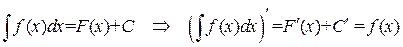 .
. .
. соответственно. Тогда сумма
соответственно. Тогда сумма 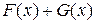 есть первообразная для функции
есть первообразная для функции  , и, следовательно, справедливо равенство
, и, следовательно, справедливо равенство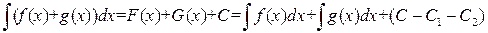 .
.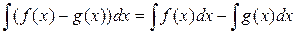 .
. .
. есть первообразная для функции
есть первообразная для функции 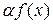 , отсюда получаем
, отсюда получаем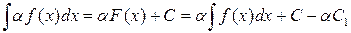 ,
, . Отсюда, по тем же причинам, что и в доказательстве свойства 3 следует справедливость свойства 4.
. Отсюда, по тем же причинам, что и в доказательстве свойства 3 следует справедливость свойства 4.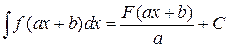 .
.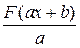 есть первообразная для функции
есть первообразная для функции 
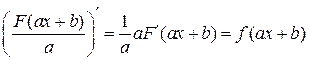 .
.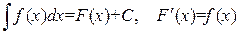 .
.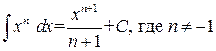 .
.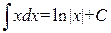 .
.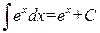 .
.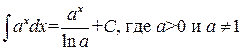 .
.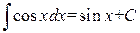 .
.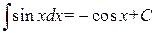 .
.
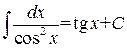 .
.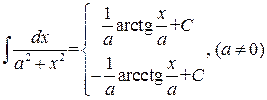 .
.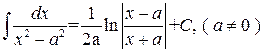 .
. .
. .
.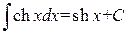 .
. .
.
 .
. . Если
. Если  , то
, то 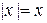 , тогда
, тогда 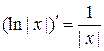 . Если
. Если  , то
, то  , тогда
, тогда 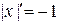 . Поэтому
. Поэтому 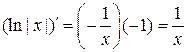 .
.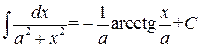 ,
,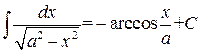 ,
, ,
,
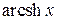 ‑ аркгиперболический синус (функция ‑ обратная к гиперболическому синусу) и
‑ аркгиперболический синус (функция ‑ обратная к гиперболическому синусу) и  ‑ аркгиперболический тангенс (функция ‑ обратная к гиперболическому тангенсу)
‑ аркгиперболический тангенс (функция ‑ обратная к гиперболическому тангенсу)


