
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция № 15. Функции нескольких переменных.Содержание книги
Поиск на нашем сайте
Вопрос 15.1. Градиент и производная по направлению функции нескольких переменных. Определение 15.1. Векторным полем называется закон, по которому каждой точке X из некоторого множества M арифметического пространства Определение 15.2. Градиентом функции нескольких переменных
Для функций 2-х и 3-х переменных градиент можно записать соответственно в виде
Замечание 15.1. Удобно точку X рассматривать как n ‑мерный вектор Градиент вектора обладает следующими двумя свойствами: Свойство 15.1. Если Доказательство очевидно. Свойство 15.2. (линейность градиента). Пусть даны два векторных поля
где Доказательство. Доказательство основано на свойстве линейности частных производных
Конец доказательства. Определение 15.3. Производной по направлению, заданным единичным вектором
Связь между градиентом и производной функцией по направлению Теорема 15.1. Если в точке
где Доказательство. Пусть
где
то полное приращение функции равно
Отсюда следует доказываемая формула. Конец доказательства. Рассмотрим свойства производной по направлению Свойство 15.1. Если Доказательство очевидно. Свойство 15.2. Изменение вектора направления на противоположный меняет знак производной по направлению
Доказательство. Формула следует из равенства
Конец доказательства. Свойство 3. (линейность производной по направлению). Пусть даны два дифференцируемых векторных поля
где Доказательство. Из теоремы 15.1 следует
Конец доказательства. Теорема 15.2. Градиент дифференцируемой функции Доказательство. Действительно, производная по направлению указывает на скорость возрастания функции в указанном направлении. Так как (
то производная по направлению будет максимальна, если Конец доказательства. Пример 15.1. Вычислить производную по направлению вектора
Вектор
Конец примера. Замечание 15.1. В некоторых случаях удобно пользоваться такими понятиями как направляющие косинусы. Под этим понимают косинус угла между направляющим вектором и соответствующей осью координат. Если
где Теорема 15.2. Градиент функции перпендикулярен линии или поверхности равного уровня. Доказательство. Ограничимся функциями 2-х переменных и докажем, что градиент перпендикулярен линии постоянного уровня, то есть в любой точке линии постоянного уровня градиент перпендикулярен касательной, проведенной к этой точке. Для функции 2-х переменных можно показать, что уравнение касательной к линии
Откуда следует, что градиент функции Определение 15.5. Нормалью к графику функции
то вектор с координатами
Пример 15.2. Для функции
тогда получаем: уравнение касательной плоскости
уравнение нормали
Конец примера.
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 392; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.63.20 (0.01 с.) |

 ставится в соответствие один и только один вектор.
ставится в соответствие один и только один вектор. называется векторное поле, определяемое по закону
называется векторное поле, определяемое по закону .
.
 .
. , то
, то  .
.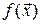 и
и  , которые имеют градиент в точке
, которые имеют градиент в точке  ,
,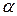 и
и  ‑ действительные числа.
‑ действительные числа.
 , в точке
, в точке  .
. .
. приращение аргумента, тогда полное приращение дифференцируемой функции равно
приращение аргумента, тогда полное приращение дифференцируемой функции равно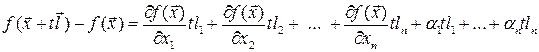 ,
, ‑ бесконечномалые функции при
‑ бесконечномалые функции при  . Так как
. Так как ,
, .
. .
. .
. .
. ,
,
 ,
, , то есть если вектор
, то есть если вектор 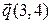 от функции
от функции  и градиент в точке M (1,3).
и градиент в точке M (1,3). .
. тогда
тогда .
. ‑ единичный вектор, то направляющие косинусы определяются из соотношения
‑ единичный вектор, то направляющие косинусы определяются из соотношения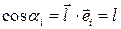 ,
, ‑ орт декартовой системы.
‑ орт декартовой системы. в точке
в точке  равно:
равно: .
. перпендикулярен вектору
перпендикулярен вектору  , то есть самой касательной.
, то есть самой касательной. в точке
в точке  плоскости имеет вид
плоскости имеет вид ,
,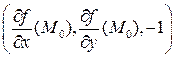 будет параллелен нормали в точке
будет параллелен нормали в точке  .
. вычислить в точке
вычислить в точке  уравнение касательной плоскости и нормали.
уравнение касательной плоскости и нормали.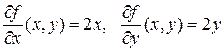 ,
, ,
, .
.


