
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция № 28. Дифференциальные уравненияСодержание книги
Поиск на нашем сайте
Вопрос 1. Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Фундаментальная система решений. Рассмотрим линейное дифференциальное однородное дифференциальное уравнение с постоянными коэффициентами
Будем искать решение этого уравнения в виде
и подставляя их в уравнение, получим
Так как
Это квадратное уравнение называется характеристическим уравнением. Рассмотрим следующие три случая:
1) характеристическое уравнение имеет разные вещественные корни, то есть его дискрименант строго положителен (D > 0). Обозначим эти корни через
Эти решения образуют Ф.С.Р., так как их определитель Вронского отличен от нуля в точке x = 0
Следовательно, общее решение этого уравнения дается формулой
2) характеристическое уравнение имеет один вещественный корень, то есть его дискрименант D = 0. В этом случае имеется одно решение
Так как D = 0, то
следовательно,
Итак фундаментальная система решений имеет вид
Общее решение уравнения есть
3) характеристическое уравнение имеет комплексные корни Тогда имеется два решения
Эти решения являются комплексными функциями вещественного аргумента x. Удобно искать решения в виде вещественных функций. Для этого используем формулы Эйлера
Тогда получим
Возьмем полусумму и полуразность этих решений
Тогда мы получим Ф.С.Р., что легко подтвердить, вычисляя определитель Вронского
Вычисляя его при x = 0, получим
Следовательно, общее решение этого уравнения имеет вид
ПРИМЕР 1. Найти общее решение уравнения Составляем характеристическое уравнение
отсюда находим общее решение уравнения
КОНЕЦ ПРИМЕРА.
ПРИМЕР 2. Найти общее решение уравнения Составляем характеристическое уравнение
отсюда находим общее решение уравнения
КОНЕЦ ПРИМЕРА.
ПРИМЕР 3. Найти общее решение уравнения Составляем характеристическое уравнение
отсюда находим общее решение уравнения Конец примера.
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 193; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.73.85 (0.008 с.) |

 .
.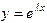 . Вычисляя производные
. Вычисляя производные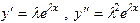
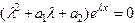
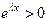 , то сокращая на, получим квадратное уравнение для определения
, то сокращая на, получим квадратное уравнение для определения .
.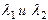 . Тогда получаем два решения
. Тогда получаем два решения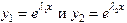
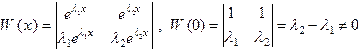
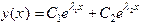 .
.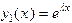 . Зная его, найдем второе решение
. Зная его, найдем второе решение 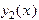 , используя формулу (смотри лекцию № 8)
, используя формулу (смотри лекцию № 8)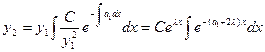
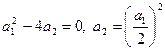 . Поэтому получаем
. Поэтому получаем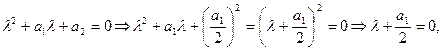
 .
.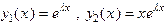
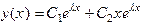
 , то есть его дискрименант D < 0.
, то есть его дискрименант D < 0.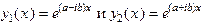 .
.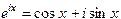 ,
,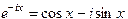 .
. ,
, ,
,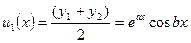
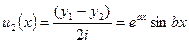
 .
.
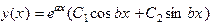
 .
.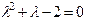 . Его корни равны
. Его корни равны  , тогда Ф.С.Р. есть
, тогда Ф.С.Р. есть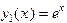 ,
, 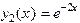 ,
,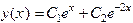 .
. .
. . Оно имеет один корень
. Оно имеет один корень 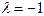 , тогда Ф.С.Р. есть
, тогда Ф.С.Р. есть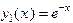 ,
, 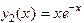 ,
,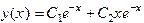 .
.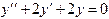 .
.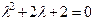 . Оно имеет комплексные корни
. Оно имеет комплексные корни 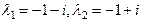 , тогда Ф.С.Р. есть
, тогда Ф.С.Р. есть ,
, 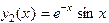 ,
,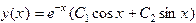 .
.


