
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция № 4 неопределенный интеграл.Содержание книги
Поиск на нашем сайте
Вопрос 4.1. Интегрирование дробно-линейных иррациональностей. Определение 4.1. Многочленом двух переменных x и y называется функция вида
Конец определения. Пример 4.1. Конец примера. Определение 4.2. Рациональной функцией двух переменных x и y называется отношение двух многочленов:
Конец определения. Пример 4.2.
Конец примера. Определение 4.3. Функция вида
называется дробно-линейной иррациональностью, где R рациональная дробь двух переменных. Конец определения. Аналогично определяются рациональные функции трех и более переменных. a) Интеграл вида вычисляется с помощью подстановки Пример 4.3. Вычислить интеграл
Конец примера. б) Интеграл вида
где Пример 4.4.
Конец примера. Вопрос 4.2. Интегрирование квадратичных иррациональностей. а) Интеграл вида выделением полного квадрата сводится к интегрированию табличных интегралов
Пример 4.5.
Конец примера. б) Интеграл вида вычисляется по методу неопределенных коэффициентов
где Пример 4.6.
Дифференцируя по x, получим
или
Конец примера. в) Интеграл вида вычисляется заменой Пример 4.7.
Конец примера. ЛЕКЦИЯ № 5 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. Вопрос 5.1. Интегрирование тригонометрических выражений. a) Интегралы вида 1) если
2) если
Пример 5.1.
Конец примера. 3)
Пример 5.2.
Конец примера. 4) Если Пример 5.3.
Конец примера. 5) Если Пример 5.4.
Конец примера. 6) Если Пример 5.5.
Конец примера.
b) Интегралы вида Для вычисления интегралов используются тригонометрические формулы:
Пример 5.6.
Конец примера. с) Интегралы вида I) Универсальная тригонометрическая подстановка
Универсальная тригонометрическая подстановка сводит интеграл к интегралу от рациональной функции: Пример 5.7.
Конец примера. II) Если выполнено равенство
Эта подстановка сводит интеграл к интегралу от рациональной функции. Пример 5.8.
Конец примера.
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 297; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.94.193 (0.01 с.) |

 .
. ‑ многочлен второй степени двух переменных.
‑ многочлен второй степени двух переменных. .
. .
. .
.
 .
. .
.
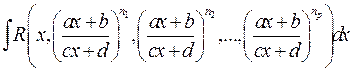
 ,
, 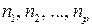 рациональные числа, вычисляется с помощью подстановки
рациональные числа, вычисляется с помощью подстановки  , где r ‑ наименьший общий знаменатель дробей
, где r ‑ наименьший общий знаменатель дробей 
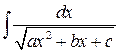
 или
или  .
.

 ,
, ‑ многочлен с неопределенными коэффициентами, - неопределенное число.
‑ многочлен с неопределенными коэффициентами, - неопределенное число. .
. ,
, , откуда A =1, =1, и, следовательно,
, откуда A =1, =1, и, следовательно,

 .
.
 .
.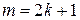 ‑ нечетное натуральное число, n ‑ любое вещественное число, то
‑ нечетное натуральное число, n ‑ любое вещественное число, то
 ‑ нечетное натуральное число, m ‑ любое вещественное число, то
‑ нечетное натуральное число, m ‑ любое вещественное число, то

 ‑ четные числа. Степени понижаются посредством перехода к двойному аргументу по формулам:
‑ четные числа. Степени понижаются посредством перехода к двойному аргументу по формулам: .
.
 , где k ‑ целое число, то делается подстановка
, где k ‑ целое число, то делается подстановка  или
или  .
. .
.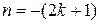 ‑ отрицательное нечетное число, n ‑ целое число, то делается подстановка
‑ отрицательное нечетное число, n ‑ целое число, то делается подстановка  .
.

 ‑ отрицательное нечетное число, m - целое число, то делается подстановка
‑ отрицательное нечетное число, m - целое число, то делается подстановка  .
.

 .
.
 , где
, где  ‑ рациональная функция двух переменных u, v.
‑ рациональная функция двух переменных u, v. ,
,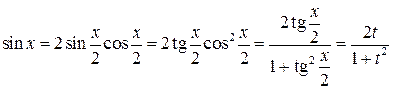 ,
, .
. .
.
 , то более подходит подстановка
, то более подходит подстановка 




