
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И.В. Терещенко И.В., А.В. БратчиковСтр 1 из 27Следующая ⇒
Кафедра общей математики И.В. Терещенко И.В., А.В. Братчиков М А Т Е М А Т И К А Часть 2 Конспект лекций для студентов заочной формы обучения факультета Нефти, Газа и Энергетики всех специальностей Краснодар УДК: Математика. Часть 2: Конспект лекций/И.В. Терещенко, А.В. Братчиков; Кубан. гос. технол. ун-т.-Краснодар: Издательство КубГТУ, 2006.-127с. ISBN……….. Рассмотрены основные вопросы курса математики по разделам «Интегральное исчисление», «Функции нескольких переменных», «Дифференциальные уравнения», изучаемые во втором семестре. Предназначено для студентов заочной формы обучения факультета Нефти, Газа и Энергетики всех специальностей. Ил. 10. Библиог.: 40 назв. Рецензенты: канд. тех. наук, Доцент Л.М. Данович; д-р тех. наук, профессор Г.Т. Вартумян © Кубанский государственный технологический университет, 2006 С О Д Е Р Ж А Н И Е ЛЕКЦИЯ № 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. …...…….………….7 Вопрос 1.1. Первообразная и неопределенный интеграл. …….…….……....7 Вопрос 1.2. Таблица интегралов. ……………………………………………..9 ЛЕКЦИЯ № 2. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. …………………...10 Вопрос 2.1. Замена переменных в неопределенном интеграле. …………..10 Вопрос 2.2. Метод интегрирования по частям. …………………………….12 ЛЕКЦИЯ № 3. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ……………….…..13 Вопрос 3.1. Рациональные дроби. …………………………………………...13 Вопрос 3.2. Разложение многочлена на множители. ………………………14 Вопрос 3.3. Разложение правильной рациональной дроби на простейшие дроби. ………………………………………………………………………….17 Вопрос 3.4. Интегрирование простейших дробей. ………………………....19 Вопрос 3.5. Примеры интегрирования рациональных дробей. …………...21 ЛЕКЦИЯ № 4 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ……………………25 Вопрос 4.1. Интегрирование дробно-линейных иррациональностей. ……25 Вопрос 4.2. Интегрирование квадратичных иррациональностей. ………...26 ЛЕКЦИЯ № 5 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ……………………28 Вопрос 5.1. Интегрирование тригонометрических выражений. …………..28 ЛЕКЦИЯ № 6. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ………………………31 Вопрос 6.1. Интегральная сумма Римана. …………………………………..31 Вопрос 6.2. Определенный интеграл. Вопрос 6.3. Свойства определенного интеграла. ЛЕКЦИЯ № 7. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
Вопрос 7.1. Аддитивность определенного интеграла. Вопрос 7.2. Основная формула интегрального исчисления (формула Ньютона ‑ Лейбница). Вопрос 7.3. Замена переменных в определенном интеграле. Вопрос 7.4. Интегрирование по частям в определенном интеграле. Вопрос 7.5. Формула Тейлора с остаточным членом в интегральной форме. ЛЕКЦИЯ № 8. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Вопрос 8.1. Формула трапеций. Вопрос 8.2. Формула прямоугольников. Вопрос 8.3. Формула Симпсона. ЛЕКЦИЯ № 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. Вопрос 9.1. Вычисление площадей плоских фигур. Вопрос 9.2. Вычисление площади криволинейного сектора. Вопрос 9.3. Вычисление объема тел. Вопрос 9.4. Площадь поверхности тела вращения. ЛЕКЦИЯ № 10 ДЛИНА ПЛОСКОЙ КРИВОЙ. Вопрос 10.1. Длина плоской кривой. Вопрос 10.2. Кривизна и радиус кривизны плоской кривой. ЛЕКЦИЯ № 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ Вопрос 11.1. Несобственные интегралы от неограниченных функций. Вопрос 11.2. Несобственные интегралы от функции, имеющие несколько особенностей. Вопрос 11.3. Главное значение несобственного интеграла. ЛЕКЦИЯ № 12. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Вопрос 12.1. Функции нескольких переменных. Основные понятия и определения. Вопрос 12.2. Предел последовательности точек в n -ом пространстве. ЛЕКЦИЯ № 13. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Вопрос 13.1. Предел функции нескольких переменных. Вопрос 13.2. Непрерывность функции нескольких переменных. Вопрос 13.3. Частные производные функции нескольких переменных. ЛЕКЦИЯ № 14. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Вопрос 14.1. Дифференциал функции нескольких переменных. Вопрос 14.2. Дифференцирование сложной функции. Инвариантность формы первого дифференциала. ЛЕКЦИЯ № 15. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Вопрос 15.1. Градиент и производная по направлению функции нескольких переменных. ЛЕКЦИЯ № 16. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Вопрос 16.1. Частные производные и дифференциалы старших порядков. Вопрос 16.2. Формула Тейлора для функции нескольких переменных. ЛЕКЦИЯ № 18. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Вопрос 18.1. Неявные функции. Вопрос 18.2. Дифференцирование неявной функции.
Конец доказательства. Определение 1.1.2. Неопределенным интегралом от функции
Конец определения. Свойства неопределенного интеграла: 1) 2) Доказательство. Доказательство следует из равенства:
Конец доказательства. 3) Доказательство. Пусть
Поскольку равенство неопределенных интегралов понимается с точностью до константы, то отсюда следует доказываемое соотношение. Конец доказательства. 4) Доказывается аналогично 3-ему свойству. 5) Доказательство. Пусть
где учтено, что Конец доказательства. 6) Доказательство. Пусть
Отсюда получаем
Конец доказательства. Вопрос 1.2. Таблица интегралов. Таблица интегралов играет в высшей математике такую же важную роль, что и таблица производных. Она состоит из наиболее часто встречающихся интегралов от элементарных функций. Эти интегралы получаются с помощью таблицы производных из определения неопределенного интеграла.
1. 2. 3.
4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. Докажем например формулу 2. Вычислим производную от Замечание 1.1. Некоторые интегралы могут быть выражены через другие функции. Например:
где Конец доказательства. Замечание 2.1. Если формулу применять слева на право, то метод называют методом замены переменных. Замечание 2.2. Если формулу применять справа налево, то метод называют методом подведения множителя под знак дифференциала. Пример 2.1. Конец примера. Пример 2.2.
Конец примера. Пример 2.3.
Конец примера. Пример 2.4.
Конец примера. Конец доказательства. Замечание 2.3. При применении метода подстановки и метода интегрирования по частям полезны выражения:
Пример 2.5. Интегралы вида
Конец примера. Пример 2.6. Интегралы вида
Конец примера. Пример 2.7. Интегралы вида Эти интегралы называются возвратными. Вычисляя их дважды по частям, получим уравнение, из которого можно найти значение интеграла.
Решая это уравнение, найдем
Конец примера. Пример 3.1.
Конец примера. Теорема 3.1. Всякую неправильную рациональную дробь можно представить в виде суммы многочлена и правильной рациональной дроби:
где Пример 3.2. Деление многочлена на многочлен уголком
Следовательно, можно записать
Конец примера. Конец доказательства. Следствие 3.1. Если a корень многочлена
Доказательство. Если a корень многочлена Конец доказательства. Следствие 3.2. Если a корень многочлена Доказательство. Согласно следствию 3.1 из теоремы Безу
Продолжая этот процесс, получим многочлен Конец доказательства. Теорема 3.4. Если Доказательство. Подставим корень a в уравнение
тогда получим
Конец доказательства. Пример 3.3. Многочлен Конец примера. Следствие 3.3. Если b комплексный корень многочлена
причем p и q - вещественные числа, r - натуральное число, такое что Доказательство. Пусть b комплексный корень, тогда согласно следствию 3.1 можно записать
Комплексно сопряженное число
Продолжая этот процесс, получим многочлен Конец доказательства. Теорема 3.6. Любой многочлен n -й степени можно разложить на множители вида
где числа k и s ‑ кратности соответствующих вещественных и мнимых корней, причем Доказательство. Согласно основной теоремы алгебры любой многочлен
Продолжая эти рассуждения уже для многочлена
где многочлен
Продолжая эти рассуждения, мы получим через конечное число шагов разложение
Многочлен Конец доказательства. Пример 3.4. Разложить многочлен
Он имеет корни Конец примера. Вопрос 3.5. Примеры интегрирования рациональных дробей. Пример 3.6. Разложим дробь на простейшие
или
1-й способ (основной):
Приравняем коэффициенты при одинаковых степенях x
отсюда 2-й способ:
Положим x равным корням знаменателя рациональной дроби, то есть положим
Отсюда получаем
Конец примера. Пример 3.7.
Разложим дробь на простые
и приведем правую часть к общему знаменателю. Приравняем числители, тогда
1-й способ:
2-й способ:
Положим x равным корню знаменателя, то есть x =1, тогда получим 2=2 B или B =1. Подставляя это в равенство, получим
или
Откуда
Положим Положим Тогда получим
Откуда получим
Конец примера. Пример 3.8.
Приведем правую часть к общему знаменателю и приравняем числители
Найдем коэффициенты 1-й способ: Раскроем скобки и сгруппируем слагаемые по степеням x
Приравнивая коэффициенты при одинаковых степенях x, получим:
Отсюда
Решая ее, найдем 2-й способ: Положим x равным корню знаменателя, то есть x =1, тогда получим
или
или
Сокращая на общий множитель
откуда Отсюда получаем разложение
Отсюда получаем
Конец примера. Пример 3.9. Для вычисления применим метод Остроградского
Дифференцируя это равенство, получим
Приведем правую часть к общему знаменателю
и приравняем числители
Сравнивая коэффициенты при старших степенях, получим:
Отсюда находим
Конец примера. Пример 4.2.
Конец примера. Определение 4.3. Функция вида
называется дробно-линейной иррациональностью, где R рациональная дробь двух переменных. Конец определения. Аналогично определяются рациональные функции трех и более переменных. a) Интеграл вида вычисляется с помощью подстановки Пример 4.3. Вычислить интеграл
Конец примера. б) Интеграл вида
где Пример 4.4.
Конец примера. Пример 4.5.
Конец примера. б) Интеграл вида вычисляется по методу неопределенных коэффициентов
где Пример 4.6.
Дифференцируя по x, получим
или
Конец примера. в) Интеграл вида вычисляется заменой Пример 4.7.
Конец примера. Пример 5.1.
Конец примера. 3)
Пример 5.2.
Конец примера. 4) Если Пример 5.3.
Конец примера. 5) Если Пример 5.4.
Конец примера. 6) Если Пример 5.5.
Конец примера. b) Интегралы вида Для вычисления интегралов используются тригонометрические формулы:
Пример 5.6.
Конец примера. с) Интегралы вида I) Универсальная тригонометрическая подстановка
Универсальная тригонометрическая подстановка сводит интеграл к интегралу от рациональной функции: Пример 5.7.
Конец примера. II) Если выполнено равенство
Эта подстановка сводит интеграл к интегралу от рациональной функции. Пример 5.8.
Конец примера. Доказательство.
Конец доказательства. Конец доказательства. Свойство 6.3. (Линейность интегральных сумм). Интегральная сумма от линейной комбинации функций
Доказательство.
Конец доказательства. Геометрический смысл интегральной суммы: интегральная сумма (см. рис. 1)
Рис. 1. Геометрический смысл интегральной суммы. Определение предела интегральных сумм функции Определение 6.3. Число I называется пределом интегральных сумм Конец определения. Предел интегральных сумм будем в дальнейшем обозначать символом
Из определения предела интегральных сумм, подобно пределу последовательности или функции, следует его единственность. Теорема 6.1. (Единственность предела интегральных сумм). Если существует предел интегральных сумм Доказательство. Предположим противное. Пусть для функции
или
Полученное противоречие доказывает теорему 6.1. Конец доказательства. Определение 6.4. Определенным интегралом от функции
при условии, что величина предела не зависит от способа разбиения отрезка Конец определения. Конец доказательства. Из теоремы 6.2. следует, неограниченные на отрезках функции не интегрируемы. Но условие ограниченности функции не является достаточным. Приведем пример ограниченной, но не интегрируемой функции. Пример 6.1. (Функция Дирихле). На отрезке Конец доказательства. Теорема 6.3. Если определенная и ограниченная на отрезке Эта теорема приводится без доказательства. Отметим, что функция Дирихле ограничена, но имеет разрыв 1-го рода в каждой точке отрезка Следствие 6.1. Непрерывная на отрезке Следствие 6.2. Кусочно-непрерывная на отрезке Приведем еще один класс интегрируемых функций. Теорема 6.4. Монотонная на отрезке Эта теорема приводится без доказательства. Замечание 6.1. Монотонная на отрезке Конец замечания. Замечание 6.2. Отметим без доказательства, что монотонная на отрезке Конец замечания.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 232; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.61.16 (0.245 с.) |
 на интервале
на интервале  называется множество всех ее первообразных, которое обозначается символом
называется множество всех ее первообразных, которое обозначается символом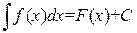 .
.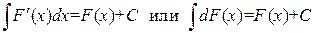 ,
, .
.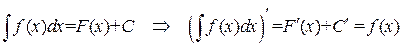 .
. .
.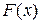 и
и 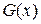 есть первообразные для функций
есть первообразные для функций  соответственно. Тогда сумма
соответственно. Тогда сумма 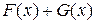 есть первообразная для функции
есть первообразная для функции  , и, следовательно, справедливо равенство
, и, следовательно, справедливо равенство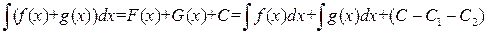 .
.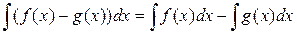 .
. .
. есть первообразная для функции
есть первообразная для функции 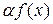 , отсюда получаем
, отсюда получаем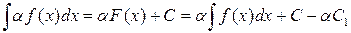 ,
, . Отсюда, по тем же причинам, что и в доказательстве свойства 3 следует справедливость свойства 4.
. Отсюда, по тем же причинам, что и в доказательстве свойства 3 следует справедливость свойства 4.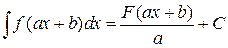 .
.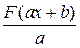 есть первообразная для функции
есть первообразная для функции 
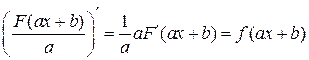 .
.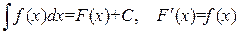 .
.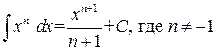 .
.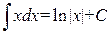 .
.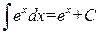 .
.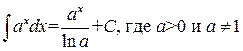 .
.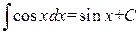 .
.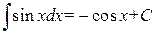 .
.
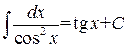 .
.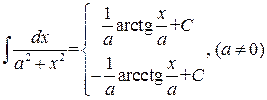 .
.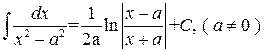 .
. .
. .
.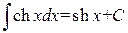 .
. .
.
 .
. . Если
. Если  , то
, то 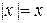 , тогда
, тогда 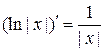 . Если
. Если  , то
, то  , тогда
, тогда 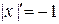 . Поэтому
. Поэтому 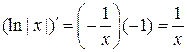 .
.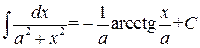 ,
,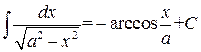 ,
, ,
,
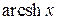 ‑ аркгиперболический синус (функция ‑ обратная к гиперболическому синусу) и
‑ аркгиперболический синус (функция ‑ обратная к гиперболическому синусу) и  ‑ аркгиперболический тангенс (функция ‑ обратная к гиперболическому тангенсу)
‑ аркгиперболический тангенс (функция ‑ обратная к гиперболическому тангенсу)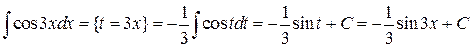 .
. .
.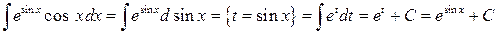 .
.
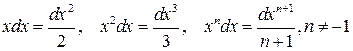 ,
, ,
,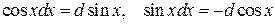 ,
,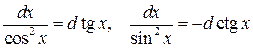 ,
,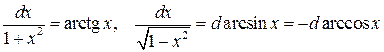 .
. , где
, где 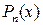 ‑ многочлен n -й степени.
‑ многочлен n -й степени.
 .
.
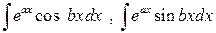 .
.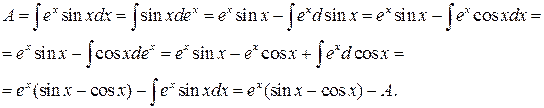
 .
. ‑ правильная рациональная дробь,
‑ правильная рациональная дробь,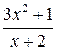 ‑ неправильная рациональная дробь,
‑ неправильная рациональная дробь, ‑ неправильная рациональная дробь.
‑ неправильная рациональная дробь.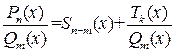 ,
,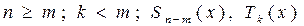 ‑ многочлены (последний из них называется остатком от деления многочлена
‑ многочлены (последний из них называется остатком от деления многочлена  на многочлен
на многочлен 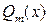 ).
).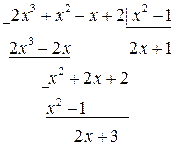
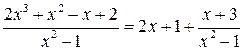 .
.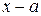 , т.e.
, т.e.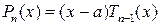 .
. и тогда r =0.
и тогда r =0. , где k натуральное число и
, где k натуральное число и 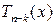 многочлен неравный 0 при
многочлен неравный 0 при  .
. , то, применяя следствие 3.1, получим
, то, применяя следствие 3.1, получим .
. ‑ многочлен n -й степени с действительными коэффициентами имеет комплексный корень a, то комплексно сопряженное к нему число
‑ многочлен n -й степени с действительными коэффициентами имеет комплексный корень a, то комплексно сопряженное к нему число  то же является корнем того же многочлена.
то же является корнем того же многочлена. и выполним комплексное сопряжение
и выполним комплексное сопряжение ,
, .
.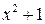 имеет корни
имеет корни  .
.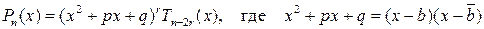 ,
, ,
,  ‑ многочлен, не равный 0 при
‑ многочлен, не равный 0 при  .
.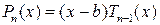 .
. будет корнем многочлена
будет корнем многочлена  . Тогда применяя к нему следствие 3.1, получим
. Тогда применяя к нему следствие 3.1, получим
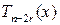 , корнем которого число b не является
, корнем которого число b не является  .
. и
и  с действительными коэффициентами:
с действительными коэффициентами: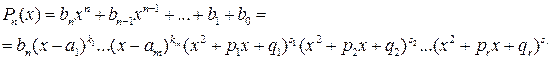
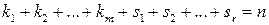 .
. . Тогда из следствия 3.3 следует, что
. Тогда из следствия 3.3 следует, что .
. , мы можем прийти через конечное число шагов к формуле
, мы можем прийти через конечное число шагов к формуле ,
, не имеет действительных корней. Тогда должен существовать комплексный корень
не имеет действительных корней. Тогда должен существовать комплексный корень  и комплексно сопряженный к нему корень
и комплексно сопряженный к нему корень  . Из следствия 3.3 получим
. Из следствия 3.3 получим .
. .
. не имеет корней и, следовательно, является константой. Значение ее легко найти, если сообразить, что она равна коэффициенту при старшей степени x. Отсюда получаем, что
не имеет корней и, следовательно, является константой. Значение ее легко найти, если сообразить, что она равна коэффициенту при старшей степени x. Отсюда получаем, что  .
. на множители с вещественными коэффициентами
на множители с вещественными коэффициентами .
. .
. .
.
 .
. .
. ,
,


 .
. ,
, .
.


 ,
, .
. .
. .
. .
.

 .
. .
.
 .
.
 и получаем систему
и получаем систему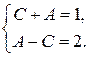
 .
. . подставляя
. подставляя  в равенство, получим
в равенство, получим

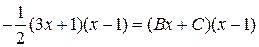 .
.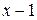 , найдем
, найдем ,
, .
. .
.
 .
. .
.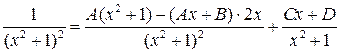 .
.
 .
.
 . Поэтому получаем
. Поэтому получаем .
. .
.
 .
. .
.
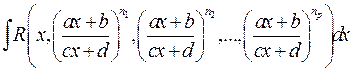
 ,
, 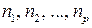 рациональные числа, вычисляется с помощью подстановки
рациональные числа, вычисляется с помощью подстановки  , где r ‑ наименьший общий знаменатель дробей
, где r ‑ наименьший общий знаменатель дробей 


 ,
, ‑ многочлен с неопределенными коэффициентами, - неопределенное число.
‑ многочлен с неопределенными коэффициентами, - неопределенное число. .
. ,
, , откуда A =1, =1, и, следовательно,
, откуда A =1, =1, и, следовательно,

 .
.

 ‑ четные числа. Степени понижаются посредством перехода к двойному аргументу по формулам:
‑ четные числа. Степени понижаются посредством перехода к двойному аргументу по формулам: .
.
 , где k ‑ целое число, то делается подстановка
, где k ‑ целое число, то делается подстановка  или
или  .
. .
.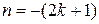 ‑ отрицательное нечетное число, n ‑ целое число, то делается подстановка
‑ отрицательное нечетное число, n ‑ целое число, то делается подстановка  .
.

 ‑ отрицательное нечетное число, m - целое число, то делается подстановка
‑ отрицательное нечетное число, m - целое число, то делается подстановка  .
.

 .
.
 , где
, где  ‑ рациональная функция двух переменных u, v.
‑ рациональная функция двух переменных u, v. ,
,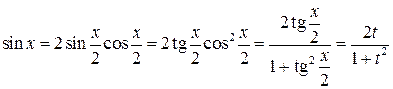 ,
, .
. .
.
 , то более подходит подстановка
, то более подходит подстановка 

 .
. есть линейная комбинация интегральных сумм этих функций.
есть линейная комбинация интегральных сумм этих функций.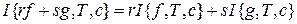 .
. . Раскрывая скобки и группируя слагаемые, получим
. Раскрывая скобки и группируя слагаемые, получим
 функции
функции  на отрезке
на отрезке  есть площадь ступенчатой фигуры, составленной из прямоугольников высотой
есть площадь ступенчатой фигуры, составленной из прямоугольников высотой  и шириной
и шириной 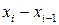 .
.
 на отрезке
на отрезке 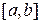 можно дать, например, на языке
можно дать, например, на языке  следующим образом.
следующим образом. функции
функции  , может быть зависящее от e, что для любого разбиения Т отрезка
, может быть зависящее от e, что для любого разбиения Т отрезка 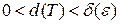 , независимо от способа разбиения отрезка
, независимо от способа разбиения отрезка 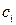 выполняется неравенство
выполняется неравенство 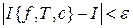 .
. .
. . Пусть выбрано
. Пусть выбрано  . Тогда должно существовать такое число
. Тогда должно существовать такое число  , что для разбиений с диаметром
, что для разбиений с диаметром  выполняются неравенства
выполняются неравенства  и
и  . Тогда
. Тогда
 .
. ,
, , если х иррационально, и
, если х иррационально, и 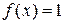 , если х рационально. Покажем, что эта функция не интегрируема по Риману, хотя она, очевидно, ограничена. Действительно, возьмем произвольное разбиение отрезка
, если х рационально. Покажем, что эта функция не интегрируема по Риману, хотя она, очевидно, ограничена. Действительно, возьмем произвольное разбиение отрезка  . Если на отрезках разбиения
. Если на отрезках разбиения  выбрать рациональные значения
выбрать рациональные значения  . Следовательно, такие интегральные суммы не имеют предела.
. Следовательно, такие интегральные суммы не имеют предела. . Следовательно, монотонные функции на отрезках удовлетворяют необходимым условиям интегрируемости (теорема 6.2).
. Следовательно, монотонные функции на отрезках удовлетворяют необходимым условиям интегрируемости (теорема 6.2).


