
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 20.1. Задачи, приводящие к дифференциальным уравнениям.
Задача 20.1. Движение материальной точки массы m под действием силы F вдоль оси X. На основании второго закона Ньютона запишем уравнение движения материальной точки:
где m ‑ масса, a ‑ ускорение, t ‑ время, x (t) - координата, Так как
Это обыкновенное дифференциальное уравнение второго порядка, описывающее закон движения материальной точки. Чтобы его определить однозначно, требуется задать начальные условия
Задача определения
называется задачей Коши. В частности, если
Задача 2. Движение материальной точки массы m в пространстве под действием силы Уравнения движения дает второй закон Ньютона:
Для однозначного решения задачи зададим начальные условия:
Тогда получаем уже систему обыкновенных дифференциальных уравнений второго порядка с начальными условиями. В векторной форме она выглядит так:
Задача 3. Радиоактивный распад. Химические реакции первого рода. Остывание нагретого тела. Скорость изменения численности популяции. Пусть m (t) ‑ количество радиоактивного вещества в момент времени t. Закон радиоактивного распада утверждает, что скорость радиоактивного распада пропорциональна количеству не распавшегося вещества, то есть
Начальное условие Решение этой задачи Коши имеет вид Пусть m (t) ‑ количество химического вещества, которое распадается по реакции A продукты реакции, и пусть скорость распада пропорциональна количеству не прореагированного вещества, тогда уравнение реакции
Начальное условие
Пятиокись азота двуокись азота Пусть некоторое тело нагрето до температуры
Пусть N - число особей в популяции, например, волков, тогда при больших N скорость изменения числа особей в популяции пропорциональна N:
Если Вывод: различные физические, химические, биологические процессы описываются одним и тем же уравнением. Задача 4. Математический маятник. Пусть на материальную точку массы m действует упругая сила
Обозначим
Задача 5. Электрические колебания в контуре.
Согласно законам Кирхгофа
Отсюда
или дифференцируя по t
Пусть
Вопрос 20.2. Основные определения и понятия теории дифференциальных уравнений. Определение 20.1. Обыкновенным дифференциальным уравнением n -го порядка называется уравнение вида:
которое содержит независимое переменное x, неизвестную функцию y (x), и ее производные вплоть до n -го порядка включительно. Дифференциальное уравнение разрешено относительно производной n -го порядка, если его можно представить в виде
Определение 20.2. Решением обыкновенного дифференциального уравнения n -го порядка называется всякая функция y (x), которая обращает его в тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием. Определение 20.3. Множество решений обыкновенного дифференциального уравнения n -го порядка вида
где Каждый выбор этих постоянных дает частное решение. График частного решения называется интегральной кривой, а множество всех интегральных кривых называется семейством интегральных кривых. Часто обыкновенное дифференциальное уравнение n‑ го порядка можно свести к уравнению вида
где Оно называется общим интегралом. Каждый выбор этих постоянных дает частный интеграл Определение 20.4. Пусть дано обыкновенное дифференциальное уравнение n -го порядка и требуется найти его решение, удовлетворяющее начальным условиям
тогда говорят, что задана задача Коши:
Для обыкновенного дифференциального уравнения 1-го порядка сформулируем теорему существования и единственности решения задачи Коши:
Теорема 20.1. Пусть функция Пример 20.1. Задача Коши
имеет единственное решение
непрерывны. Пример 20.2. Задача Коши
имеет два решения
терпит разрыв в точке (0,0). Поэтому условия применимости теоремы 1 нарушены. Возможность существования нескольких решений задачи Коши определяется теоремой Пеано. Теорема 20.2. (Пеано) Если
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.31.247 (0.014 с.) |
 ,
, ‑ скорость.
‑ скорость.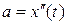 , то
, то .
.
 из
из
 , то решение задачи Коши имеет вид:
, то решение задачи Коши имеет вид: .
. .
.


 .
. .
. .
.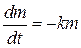 .
.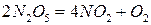 .
. и оставлено остывать. Согласно закону Ньютона скорость остывания пропорциональна температуре тела, то есть
и оставлено остывать. Согласно закону Ньютона скорость остывания пропорциональна температуре тела, то есть

 , то
, то  , если
, если  , то
, то  при
при  .
. , тогда по закону Ньютона
, тогда по закону Ньютона
 , тогда получим уравнение свободных колебаний
, тогда получим уравнение свободных колебаний .
.
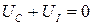 ,
, .
.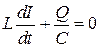 ,
, .
. , тогда после деления на L получим
, тогда после деления на L получим .
. ,
, .
. ,
, ‑ произвольные постоянные, называется общим решением.
‑ произвольные постоянные, называется общим решением. ,
, .
. ,
,
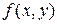 непрерывна в замкнутой области D переменных
непрерывна в замкнутой области D переменных  , содержащей точку
, содержащей точку 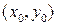 , тогда, если частная производная этой функции по y непрерывна на этом множестве, то задача Коши на некотором отрезке
, тогда, если частная производная этой функции по y непрерывна на этом множестве, то задача Коши на некотором отрезке  имеет решение и это решение единственное.
имеет решение и это решение единственное.
 , так как в любой замкнутой области, содержащей точку (0,1) функция
, так как в любой замкнутой области, содержащей точку (0,1) функция  и ее частная производная по y
и ее частная производная по y
 .
. и
и  . Правая часть уравнения
. Правая часть уравнения  непрерывна в любой окрестности точки (0,0), но производная по y
непрерывна в любой окрестности точки (0,0), но производная по y
 непрерывна на замкнутой области D переменных x, y, то при условии, что точка
непрерывна на замкнутой области D переменных x, y, то при условии, что точка 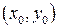 принадлежит этой области, задача Коши имеет хотя бы одно решение в некоторой окрестности точки
принадлежит этой области, задача Коши имеет хотя бы одно решение в некоторой окрестности точки  .
.


