
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция № 25. Дифференциальные уравнения.
Вопрос 25.1. Метод Рунге-Кутта. Пусть
Тогда при малых значениях h имеем приближенную формулу:
Эту формулу можно положить в основу численного метода
где
и т.д. Метод (3) называют методом p -го порядка. Чем выше порядок метода, тем он точнее и можно брать более крупный шаг h. Метод Эйлера имеет порядок
где
Параметры Пример 25.1. Метод Рунге-Кутта 2-го порядка. Требуется получить семейство методов 2-го порядка. Пусть
Разложим
Отсюда, чтобы получить метод второго порядка, необходимо выполнение равенств
Тогда получим
Тогда получаем семейство методов Рунге-Кутта 2-го порядка
Наиболее часто используется схема предиктор-корректор a=1
а так же усовершенствованный метод Эйлера
Конец примера. Наиболее часто используется метод Рунге - Кутта 4-го порядка
Для оценки погрешности разностного метода существует эмпирическое правило Рунге: Если
Составим таблицу: Метод Эйлера Метод Рунге - Кутта второго порядка Метод Рунге - Кутта четвертого порядка Полученное решение можно уточнить по формуле Ричардсона
повысив порядок метода еще на единицу. Пример 25.2. Найти численное решение задачи Коши методом Рунге-Кутта второго порядка (схема предиктор - корректор)
Пусть h = 0.25, результаты расчетов приведем в таблице
Таблица 1.
Пусть h = 0.125, результаты расчетов приведем в таблице
Таблица 2. (
Конец примера.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.198.49 (0.006 с.) |
 есть точное решение задачи Коши. Если
есть точное решение задачи Коши. Если  имеет непрерывные производные вплоть до n -го порядка включительно, то
имеет непрерывные производные вплоть до n -го порядка включительно, то 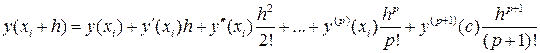 .
. .
.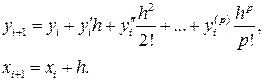 (1)
(1)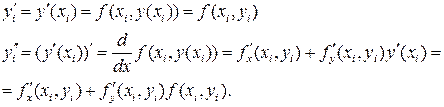
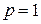 , он самый простейший и поэтому его точность часто недостаточно велика, и необходимо использовать методы более высоких порядков или брать очень маленькие величины h. С ростом p вычисление производных быстро усложняется и метод (1) поэтому не находит применения при значениях
, он самый простейший и поэтому его точность часто недостаточно велика, и необходимо использовать методы более высоких порядков или брать очень маленькие величины h. С ростом p вычисление производных быстро усложняется и метод (1) поэтому не находит применения при значениях 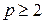 . Вместо этого метода, Рунге и Кутт предложили другой метод, наиболее распространенный в наше время. Если в i -м узле
. Вместо этого метода, Рунге и Кутт предложили другой метод, наиболее распространенный в наше время. Если в i -м узле  известно, то решение в этом узле берут в виде
известно, то решение в этом узле берут в виде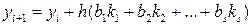 (2)
(2)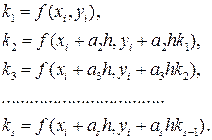
 выбирают так, чтобы метод имел требуемый порядок p, то есть, чтобы при разложении (2) по степеням h это разложение совпадало с (1) до степени
выбирают так, чтобы метод имел требуемый порядок p, то есть, чтобы при разложении (2) по степеням h это разложение совпадало с (1) до степени 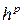 включительно.
включительно.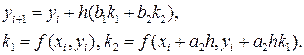
 по формуле Тейлора до слагаемых порядка h
по формуле Тейлора до слагаемых порядка h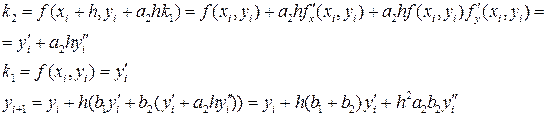
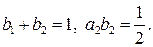

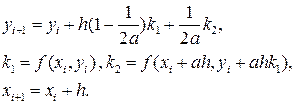
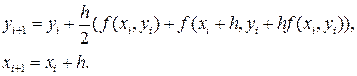
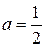
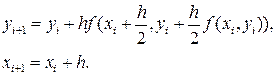
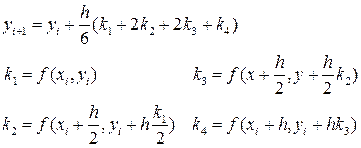
 - решение, полученное на сетке с шагом h, а
- решение, полученное на сетке с шагом h, а 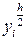 - решение, полученное на сетке с шагом
- решение, полученное на сетке с шагом  , то в общих узлах погрешность вычислений приближенно равна
, то в общих узлах погрешность вычислений приближенно равна , где p порядок метода.
, где p порядок метода.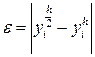
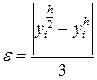 .
.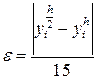 .
.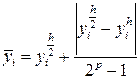 ,
,


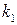
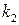
 ‑ уточнение по Ричардсону)
‑ уточнение по Ричардсону)



