Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрица выигрышей. Представление игр в нормальной формеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Игрой в нормальной форме называется совокупность Обычно игроков нумеруют в произвольном порядке от 1 до n (n — число игроков), поэтому N={1,2,...,n}. Стратегия i— го игрока для игры в нормальной форме сводится к одноактному выбору любой точки из множества Ui. Функция выигрыша ставит в соответствие каждому элементу и=(u1,...,un) из множества Исходная постановка игры в нормальной форме не предполагает никакой дополнительной информации у игроков о действиях друг друга. Поэтому можно считать, что все игроки одновременно и независимо осуществляют выбор своих стратегий, т.е. элементов ui ∈ Ui. В результате складывается ситуация и, однозначно определяющая выигрыши всех игроков g1(u),...gn(u). Рассмотрим парную игру с игроками А и В. Пусть игрок А имеет т стратегий Если каждый из игроков А и В сознательно определенным образом выбирает стратегии Аi и Вj соответственно, то сложившаяся ситуация (в чистых стратегиях) (Аi,Bj) однозначно определяет выигрыш игрока А, выражающийся действительным числом аij, которое одновременно является и проигрышем игрока В. А число (- aij) выражает проигрыш игрока А и выигрыш игрока В. Если число aij отрицательно, то в принятой нами формализованной терминологии оно будет представлять отрицательный выигрыш игрока А, а по сути - его проигрыш. Числа аij - это значения функции выигрыша FA игрока A: FA(i, j) = FA(Ai, Bj) = аij. Ходы игроков с сознательным выбором одной из возможных своих чистых стратегий называют иногда личными ходами. Выигрыши aij, i = 1,..., m, j = 1,..., n, можно расположить в виде матрицы, номера строк которой соответствуют номерам стратегий игрока А, а номера столбцов - номерам стратегий игрока В.
Матрица А называется матрицей выигрышей игрока A. Обозначим через bij значения функции выигрыша FB игрока В, т. е. FB(j, i) = FB(Вj, Ai) = bji, j = 1,..., n, i = 1,..., т. Тогда матрица выигрышей игрока В будет иметь вид
Если рассматриваемая игра - антагонистическая (т.е. с нулевой суммой выигрышей), то функции выигрышей FA и FB игроков А и В связаны между собой равенством F B(Bj, Ai) = - FA(Ai, Bj), i = 1, …, m, j = 1,..., n и, следовательно, bji = FB(Bj, Аi) = -FA(A i , Bj) = -аij, i = 1,..., т, j = 1,..., n. Эти равенства означают, что матрица выигрышей В игрока В является противоположной транспонированной матрице A: B = - A T. Таким образом, матрица В вполне определяется матрицей А. Матрицу А также называют матрицей игры, или платежной матрицей. Матрица А имеет размер т × п, где первая компонента размера т указывает на число строк (т.е. число стратегий игрока А), а вторая п - на число столбцов (число стратегий игрока В). Поэтому часто такую игру называют т × п - игрой. Отметим, что матрица игры существенно зависит от упорядочений множеств Всякую конечную антагонистическую игру можно привести к матричной форме. Матрица игры А формируется в зависимости от значений функции выигрыша FA, которая может задаваться таблично, аналитически (в виде формулы) или словесно-описательным способом. Максиминный принцип игры Рассмотрим матричную т × п - игру с игроками А и В,в которой игрок А обладает т чистыми стратегиями
Перед игроком А стоит задача выбора чистой стратегии из множества аi 1, аi 2, …, аin, расположенных в i -й строке матрицы выигрышей, в зависимости от выбранной игроком В стратегии. Предполагая поведение игрока А крайне осмотрительным, необходимо считать, что игрок В сыграет наилучшим для себя образом и на выбор игроком А стратегии Аi выберет ту стратегию Bj, при которой выигрыш игрока А окажется минимальным. Обозначим минимальный среди выигрышей аi 1, аi 2, …, аin через α i:
и назовем его показателем эффективности стратегии Аi. Продолжая действовать разумно, игрок А должен выбрать ту стратегию, которая максимизирует показатель эффективности, т.е. для которой число α i максимально. Если обозначить это максимальное число через α:
то по формуле
Описанный принцип выбора эффективной стратегии игроком А называется максиминным принципом, а выигрыш α - максимином. Пусть игрок А выбрал максиминную стратегию
Это неравенство означает, что если игрок А в игре будет следовать максиминной стратегии, то ему при любой игре противника В гарантирован выигрыш в чистых стратегиях, не меньший максимина α.
Минимаксный принцип игры Рассмотрим матричную т × п - игру с игроками А и В,в которой игрок А обладает т чистыми стратегиями
Рассмотрим игру с точки зрения игрока В, который стремится минимизировать выигрыш игрока А, исходя из посылки, что игрок А играет наилучшим для себя и наихудшим для игрока В образом. Если игрок В выберет стратегию а 1 j , а 2 j , …, аmj, (1) выигрышей, стоящих в j -м столбце матрицы выигрышей, в зависимости от того, какой стратегии будет придерживаться игрок А. Но так как игрок В предполагает, что игрок А играет наилучшим для себя образом, то выигрышем игрока А будет максимальное из чисел (1); обозначим его через βj:
и назовем показателем неэффективности стратегии Вj. Таким образом, для любой стратегии Bj игрока В наибольший его проигрыш равен β j. В интересах игрока В - выбрать стратегию с минимальным показателем неэффективности. Наименьшее из чисел (2) обозначим β:
Отсюда в силу формулы (2) получим для β выражение:
Критерий выбора эффективной стратегии для игрока В называется минимаксным принципом, а выигрыш β называется минимаксом.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-27; просмотров: 961; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.86.5 (0.029 с.) |

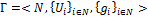 , где N - множество всех игроков; Ui - множество стратегий i— го игрока; gi - функция выигрыша i — го игрока, которую он стремится максимизировать.
, где N - множество всех игроков; Ui - множество стратегий i— го игрока; gi - функция выигрыша i — го игрока, которую он стремится максимизировать.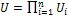 называемому исходом или ситуацией игры, действительное число. Таким образом, gi есть однозначное отображение множества U→R.
называемому исходом или ситуацией игры, действительное число. Таким образом, gi есть однозначное отображение множества U→R.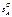 ={А1, A2,..., Ат}, а (противник) игрок В - п стратегий
={А1, A2,..., Ат}, а (противник) игрок В - п стратегий 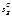 ={В1, B2,..., Вп}. Натуральные числа т и п в общем случае никак не связаны между собой.
={В1, B2,..., Вп}. Натуральные числа т и п в общем случае никак не связаны между собой.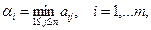
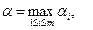
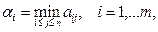
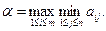
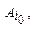 а игрок В - какую-то произвольную стратегию Bl, l = 1,..., п. Тогда в создавшейся ситуации (
а игрок В - какую-то произвольную стратегию Bl, l = 1,..., п. Тогда в создавшейся ситуации (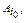 Bl) выигрыш игрока А в чистых стратегиях будет
Bl) выигрыш игрока А в чистых стратегиях будет 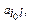 для которого в силу равенств
для которого в силу равенств 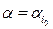 будет справедливо неравенство
будет справедливо неравенство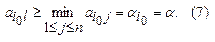
 , то выигрышем игрока А может быть один из
, то выигрышем игрока А может быть один из