
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Игра – математическая модель антогонистической ситуацииСодержание книги
Поиск на нашем сайте
Игрой называется математическая модель конфликтной ситуации. Раздел теории исследований операций, занимающейся математическими моделями принятия оптимальных решений в условиях конфликта, называется теорией игр. Заинтересованные стороны в игре называются игроками. Любое возможное в игре действие игрока называется его чистой стратегией. Игра называется конечной, если множество стратегий каждого игрока конечно. Чаще степень удовлетворения интересов игрока А характеризуется его функцией выигрыша Аналогично, для игрока В функция выигрыша Основной целью теории игр является выработка рекомендаций для удовлетворительного поведения игроков в конфликте, то есть выявления для каждого из них «оптимальных стратегий». Оптимальной называется стратегия, которая при многократно повторяющейся игре гарантирует игроку максимально возможный средний выигрыш (или эквивалентно минимальный возможный средний проигрыш). Выбор оптимальной стратегии базируется на принципе, предполагающем, что оба игрока разумны в одинаковой степени и поведение каждого из них направлено на противодействие противнику в достижении его цели. Таким образом, теория игр абстрагируется от ошибок, просчетов, азарта и риска, присущих игрокам в реальных случаях. Если в парной игре игроки преследуют противоположные цели, то игра называется антагонистической. В такой игре один из игроков выигрывает ровно столько, сколько проигрывает другой. Поэтому, функции выигрышей В силу равенства В конечной антагонистической игре с игроками А и В можно строки некоторой матрицы поставить в соответствие стратегиям Аналогичным образом, из значений
|
||||
|
Последнее изменение этой страницы: 2017-01-27; просмотров: 306; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.157.231 (0.015 с.) |

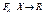 , определенной на множестве
, определенной на множестве  всех ситуаций и ставящий в соответствие каждой ситуации
всех ситуаций и ставящий в соответствие каждой ситуации 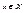 некоторое число
некоторое число  , называемое выигрышем игрока А в ситуации x.
, называемое выигрышем игрока А в ситуации x. определена на множестве
определена на множестве  ситуаций
ситуаций  и каждый из них ставит в соответствие число
и каждый из них ставит в соответствие число  , называемое выигрышем игрока В в ситуации y.
, называемое выигрышем игрока В в ситуации y. соответственно игроков А и В связаны между собой соотношением
соответственно игроков А и В связаны между собой соотношением  Из этого равенства следует, что
Из этого равенства следует, что  и потому антагонистические игры называют играми двух сторон с нулевой суммой выигрыша.
и потому антагонистические игры называют играми двух сторон с нулевой суммой выигрыша. функция выигрыша игрока В полностью определяется функцией выигрыша игрока А и, следовательно, антагонистическая игра с игроками А и В определяется совокупностью
функция выигрыша игрока В полностью определяется функцией выигрыша игрока А и, следовательно, антагонистическая игра с игроками А и В определяется совокупностью  , состоящей из множества
, состоящей из множества  чистых стратегий игрока А, множества
чистых стратегий игрока А, множества 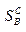 чистых стратегий игрока В и функции
чистых стратегий игрока В и функции  выигрыша игрока А.
выигрыша игрока А. игрока А, а столбцы – в соответствие стратегиям
игрока А, а столбцы – в соответствие стратегиям  игрока В. Если на пересечениях строк и столбцов расставить значения
игрока В. Если на пересечениях строк и столбцов расставить значения  функции выигрыша
функции выигрыша  , то получим матрицу А, которая называется матрицей выигрышей игрока А.
, то получим матрицу А, которая называется матрицей выигрышей игрока А. функции выигрыша
функции выигрыша  игрока В, можно составить матрицу В выигрышей игрока В. В силу равенства
игрока В, можно составить матрицу В выигрышей игрока В. В силу равенства 
 . Таким образом, матрица В определяется матрицей А и потому конечная антагонистическая игра характеризуется фактически только одной матрицей выигрышей и в силу этого называется матричной.
. Таким образом, матрица В определяется матрицей А и потому конечная антагонистическая игра характеризуется фактически только одной матрицей выигрышей и в силу этого называется матричной.


